A third ACM webinar this year (after two on agile methods): I will be providing a general introduction to Design by Contract. The date is this coming Thursday, September 17, and the time is noon New York (18 Paris/Zurich, 17 London, 9 Los Angeles, see here for hours elsewhere). Please tune in! The event is free but requires registration here.
Concurrency
New paper: Theory of Programs
Programming, wrote Dijkstra many years ago, is a branch of applied mathematics. That is only half of the picture: the other half is engineering, and this dual nature of programming is part of its attraction.
Descriptions of the mathematical side are generally, in my view, too complicated. This article [1] presents a mathematical theory of programs and programming based on concepts taught in high school: elementary set theory. The concepts covered include:
- Programming.
- Specification.
- Refinement.
- Non-determinism.
- Feasibility.
- Correctness.
- Programming languages.
- Kinds of programs: imperative, functional, object-oriented.
- Concurrency (small-step and large-step)
- Control structures (compound, if-then-else and Dijkstra-style conditional, loop).
- State, store and environment.
- Invariants.
- Notational conventions for building specifications and programs incrementally.
- Loop invariants and variants.
One of the principal ideas is that a program is simply the description of a mathematical relation. The program text is a rendering of that relation. As a consequence, one may construct programming languages simply as notations to express certain kinds of mathematics. This approach is the reverse of the usual one, where the program text and its programming languages are the starting point and the center of attention: theoreticians develop techniques to relate them to mathematical concepts. It is more effective to start from the mathematics (“unparsing” rather than parsing).
All the results (74 properties expressed formally, a number of others in the text) are derived as theorems from rules of elementary set theory; there are no new axioms whatsoever.
The paper also has a short version [2], omitting proofs and many details.
References
[1] Theory of Programs, available here.
[2] Theory of Programs, short version of [1] (meant for quick understanding of the ideas, not for publication), available here.
Detecting deadlock automatically? (New paper)
To verify sequential programs, we have to prove that they do the right thing, but also that they do it within our lifetime — that they terminate. The termination problem is considerably harder with concurrent programs, since they add a new form of non-termination: deadlock. A set of concurrent processes or threads will deadlock if they end up each holding a resource that another wants and wanting a resource that another holds.
There is no general solution to the deadlock problem, even a good enough general solution. (“Good enough” is the best we can hope for, since like many important problems deadlock is undecidable.) It is already hard enough to provide run-time deadlock detection, to be able at least to cancel execution when deadlock happens. The research reported in this new paper [1] pursues the harder goal of static detection. It applies to an object-oriented context (specifically the SCOOP model of concurrent OO computation) and relies fundamentally on the alias calculus, a static alias analysis technique developed in previous publications.
The approach is at its inception and considerable work remains to be done. Still, the example handled by the paper is encouraging: analyzing two versions of the dining philosophers problem and proving — manually — that one can deadlock and the other cannot.
References
[1] Bertrand Meyer: An automatic technique for static deadlock prevention, in PSI 2014 (Ershov Informatics Conference), eds. Irina Virbitskaite and Andrei Voronkov, Lecture Notes in Computer Science, Springer, 2015, to appear.; draft available here.
Lampsort
In support of his view of software methodology, Leslie Lamport likes to use the example of non-recursive Quicksort. Independently of the methodological arguments, his version of the algorithm should be better known. In fact, if I were teaching “data structures and algorithms” I would consider introducing it first.
As far as I know he has not written down his version in an article, but he has presented it in lectures; see [1]. His trick is to ask the audience to give a non-recursive version of Quicksort, and of course everyone starts trying to remove the recursion, for example by making the stack explicit or looking for invertible functions in calls. But his point is that recursion is not at all fundamental in Quicksort. The recursive version is a specific implementation of a more general idea.
Lamport’s version — let us call it Lampsort —is easy to express in Eiffel. We may assume the following context:
a: ARRAY [G -> COMPARABLE] — The array to be sorted.
pivot: INTEGER — Set by partition.
picked: INTEGER_INTERVAL — Used by the sorting algorithm, see below.
partition (i, j: INTEGER)
……..require — i..j is a sub-interval of the array’s legal indexes:
……..……..i < j
……..……..i >= a.lower
……..……..j <= a.upper
……..do
……..……..… Usual implementation of partition …
……..ensure — The expected effect of partition:
……..……..pivot >= i
……..……..pivot < j
……..……..— a [i..j] has been reshuffled so that elements in i..pivot are less than
……..……..— or equal to those in pivot+1 .. j.
……..end
We do not write the implementation of partition since the point of the present discussion is the overall algorithm. In the usual understanding, that algorithm consists of doing nothing if the array has no more than one element, otherwise performing a partition and then recursively calling itself on the two resulting intervals. The implementation can take advantage of parallelism by forking the recursive calls out to different processors. That presentation, says Lamport, describes only a possible implementation. The true Quicksort is more general. The algorithm works on a set not_sorted of integer intervals i..j such that the corresponding array slices a [i..j] are the only ones possibly not sorted; the goal of the algorithm is to make not_sorted empty, since then we know the entire array is sorted. In Eiffel we declare this set as:
not_sorted: SET [INTEGER_INTERVAL]
The algorithm initializes not_sorted to contain a single element, the entire interval; at each iteration, it removes an interval from the set, partitions it if that makes sense (i.e. the interval has more than one element), and inserts the resulting two intervals into the set. It ends when not_sorted is empty. Here it is:
……..from — Initialize interval set to contain a single interval, the array’s entire index range:
……..…..create not_sorted.make_one (a.lower |..| a.upper)…. ..……..
……..invariant
……..…..— See below
……..until
……..…..not_sorted.is_empty — Stop when there are no more intervals in set
……..loop
……..…..picked := not_sorted.item — Pick an interval from (non-empty) interval set.
……..……if picked.count > 1 then — (The precondition of partition holds, see below.)
……..……..…..partition (picked.lower, picked.upper) — Split: move small items before & large ones after pivot.
……..……..…..not_sorted.extend (picked.lower |..| pivot) — Insert new intervals into the set of intervals: first
……..……....…not_sorted.extend (pivot + 1 |..| picked.upper) — and second.
……..……end
……..…...not_sorted.remove (picked) — Remove interval that was just partitioned.
…….end
Eiffel note: the function yielding an integer interval is declared in the library class INTEGER using the operator |..| (rather than just ..).
The query item from SET, with the precondition not is_empty, returns an element of the set. It does not matter which element. In accordance with the Command-Query Separation principle, calling item does not modify the set; to remove the element you have to use the command remove. The command extend adds an element to the set.
The abstract idea behind Lampsort, explaining why it works at all, is the following loop invariant (see [2] for a more general discussion of how invariants provide the basis for understanding loop algorithms). We call “slice” of an array a non-empty contiguous sub-array; for adjacent slices we may talk of concatenation; also, for slices s and t, s <= t means that every element of s is less than or equal to every element of t. The invariant is:
a is the concatenation of the members of a set slices of disjoint slices, such that:
– The elements of a are a permutation of its original elements.
– The index range of any member of slices having more than one element is in not_sorted.
– For any adjacent slices s and t (with s before t), s <= t.
The first condition (conservation of the elements modulo permutation) is a property of partition, the only operation that can modify the array. The rest of the invariant is true after initialization (from clause) with slices made of a single slice, the full array. The loop body maintains it since it either removes a one-element interval from not_sorted (slices loses the corresponding slice) or performs partition with the effect of partitioning one slice into two adjacent ones satisfying s <= t, whose intervals replace the original one in not_sorted. On exit, not_sorted is empty, so slices is a set of one-element slices, each less than or equal to the next, ensuring that the array is sorted.
The invariant also ensures that the call to partition satisfies that routine’s precondition.
The Lampsort algorithm is a simple loop; it does not use recursion, but relies on an interesting data structure, a set of intervals. It is not significantly longer or more difficult to understand than the traditional recursive version
sort (i, j: INTEGER)
……..require
……..……..i <= j
……..……..i >= a.lower
……..……..j <= a.upper
……..do
……..……if j > i then — Note that precondition of partition holds.
……..……..…..partition (i, j) — Split into two slices s and t such that s <= t.
……..……..…..sort (i, pivot) — Recursively sort first slice.
……..……..…..sort (pivot+1, j) — Recursively sort second slice.
……..……end……..…..
……..end
Lampsort, in its author’s view, captures the true idea of Quicksort; the recursive version, and its parallelized variants, are only examples of possible implementations.
I wrote at the start that the focus of this article is Lampsort as an algorithm, not issues of methodology. Let me, however, give an idea of the underlying methodological debate. Lamport uses this example to emphasize the difference between algorithms and programs, and to criticize the undue attention being devoted to programming languages. He presents Lampsort in a notation which he considers to be at a higher level than programming languages, and it is for him an algorithm rather than a program. Programs will be specific implementations guided in particular by efficiency considerations. One can derive them from higher-level versions (algorithms) through refinement. A refinement process may in particular remove or restrict non-determinism, present in the above version of Lampsort through the query item (whose only official property is that it returns an element of the set).
The worldview underlying the Eiffel method is almost the reverse: treating the whole process of software development as a continuum; unifying the concepts behind activities such as requirements, specification, design, implementation, verification, maintenance and evolution; and working to resolve the remaining differences, rather than magnifying them. Anyone who has worked in both specification and programming knows how similar the issues are. Formal specification languages look remarkably like programming languages; to be usable for significant applications they must meet the same challenges: defining a coherent type system, supporting abstraction, providing good syntax (clear to human readers and parsable by tools), specifying the semantics, offering modular structures, allowing evolution while ensuring compatibility. The same kinds of ideas, such as an object-oriented structure, help on both sides. Eiffel as a language is the notation that attempts to support this seamless, continuous process, providing tools to express both abstract specifications and detailed implementations. One of the principal arguments for this approach is that it supports change and reuse. If everything could be fixed from the start, maybe it could be acceptable to switch notations between specification and implementation. But in practice specifications change and programs change, and a seamless process relying on a single notation makes it possible to go back and forth between levels of abstraction without having to perform repeated translations between levels. (This problem of change is, in my experience, the biggest obstacle to refinement-based approaches. I have never seen a convincing description of how one can accommodate specification changes in such a framework without repeating the whole process. Inheritance, by the way, addresses this matter much better.)
The example of Lampsort in Eiffel suggests that a good language, equipped with the right abstraction mechanisms, can be effective at describing not only final implementations but also abstract algorithms. It does not hurt, of course, that these abstract descriptions can also be executable, at the possible price of non-optimal performance. The transformation to an optimal version can happen entirely within the same method and language.
Quite apart from these discussions of software engineering methodology, Lamport’s elegant version of Quicksort deserves to be known widely.
References
[1] Lamport video here, segment starting at 0:32:34.
[2] Carlo Furia, Bertrand Meyer and Sergey Velder: Loop invariants: Analysis, Classification and Examples, in ACM Computing Surveys, September 2014, preliminary text here.
New article: passive processors
The SCOOP concurrency model has a clear division of objects into “regions”, improving the clarity and reliability of concurrent programs by establishing a close correspondence between the object structure and the process structure. Each region has an associated “processor”, which executes operations on the region’s objects. A literal application of this rule implies, however, a severe performance penalty. As part of the work for his PhD thesis (defended two weeks ago), Benjamin Morandi found out that a mechanism for specifying certain processors as “passive” yields a considerable performance improvement. The paper, to be published at COORDINATION, describes the technique and its applications.
Reference
Benjamin Morandi, Sebastian Nanz and Bertrand Meyer: Safe and Efficient Data Sharing for Message-Passing Concurrency, to appear in proceedings of COORDINATION 2014, 16th International Conference on Coordination Models and Languages, Berlin, 3-6 June 2014, draft available here.
.
LASER 2014 (Elba, September)
2014 marks the 10-th anniversary (11th edition) of the LASER summer school. The school will be held September 7-14, 2014, and the detailed information is here.
LASER (the name means Laboratory for Applied Software Engineering Research) is dedicated to practical software engineering. The roster of speakers since we started is a who’s who of innovators in the field. Some of the flavor of the school can gathered from the three proceedings volumes published in Springer LNCS (more on the way) or simply by browsing the pages of the schools from previous years.
Usually we have a theme, but to mark this anniversary we decided to go for speakers first; we do have a title, “Leading-Edge Software Engineering”, but broad enough to encompass a wide variety of a broad range of topics presented by star speakers: Harald Gall, Daniel Jackson, Michael Jackson, Erik Meijer (appearing at LASER for the third time!), Gail Murphy and Moshe Vardi. With such a cast you can expect to learn something important regardless of your own primary specialty.
LASER is unique in its setting: a 5-star hotel in the island paradise of Elba, with outstanding food and countless opportunities for exploring the marvelous land, the beaches, the sea, the geology (since antiquity Elba has been famous for its stones and minerals) and the history, from the Romans to Napoleon, who in the 9 months of his reign changed the island forever. The school is serious stuff (8:30 to 13 and 17 to 20 every day), but with enough time to enjoy the surroundings.
Registration is open now.
PhD positions in concurrency/distribution/verification at ETH
As part of our “Concurrency Made Easy” ERC Advanced Investigator Grant project (2012-2017), we are offering PhD positions at the Chair of Software Engineering of ETH Zurich. The goal of the project is to build a sophisticated programming and verification architecture to make concurrent and distributed programming simple and reliable, based on the ideas of Eiffel and particularly the SCOOP concurrency model. Concurrency in its various forms (particularly multithreading) as well as distributed computing are required for most of today’s serious programs, but programming concurrent applications remains a challenge. The CME project is determined to break this complexity barrier. Inevitably, achieving simplicity for users (in this case, application programmers) requires, under the hood, a sophisticated infrastructure, both conceptual (theoretical models) and practical (the implementation). We are building that infrastructure.
ETH offers an outstanding research and education environment and competitive salaries for “assistants” (PhD students), who are generally expected in addition to their research to participate in teaching, in particular introductory programming, and other activities of the Chair. The candidates we seek have: a master’s degree in computer science or related field from a recognized institution (as required by ETH); a strong software engineering background, both practical and theoretical, and more generally a strong computer science and mathematical culture; a good knowledge of verification techniques (e.g. Hoare-style, model-checking, abstract interpretation); some background in concurrency or distribution; and a passion for high-quality software development. Prior publications, and experience with Eiffel, are pluses. In line with ETH policy, particular attention will be given to female candidates.
Before applying, you should become familiar with our work; see in particular the research pages at se.ethz.ch including the full description of the CME project at cme.ethz.ch.
Candidates should send (in PDF or text ) to se-open-positions@lists.inf.ethz.ch a CV and a short cover letter describing their view of the CME project and ideas about their possible contribution.
Concurrency video
Our Concurrency Made Easy project, the result of an ERC Advanced Investigator Grant, is trying to solve the problem of making concurrent programming simple, reliable and effective. It has spurred related efforts, in particular the Roboscoop project applying concurrency to robotics software.
Sebastian Nanz and other members of the CME project at ETH have just produced a video that describes the aims of the project and presents some of the current achievements. The video is available on the CME project page [1] (also directly on YouTube [2]).
References
[1] Concurrency Made Easy project, here.
[2] YouTube CME video, here.
LASER summer school: Software for the Cloud and Big Data
The 2013 LASER summer school, organized by our chair at ETH, will take place September 8-14, once more in the idyllic setting of the Hotel del Golfo in Procchio, on the island of Elba in Italy. This is already the 10th conference; the roster of speakers so far reads like a who’s who of software engineering.
The theme this year is Software for the Cloud and Big Data and the speakers are Roger Barga from Microsoft, Karin Breitman from EMC, Sebastian Burckhardt from Microsoft, Adrian Cockcroft from Netflix, Carlo Ghezzi from Politecnico di Milano, Anthony Joseph from Berkeley, Pere Mato Vila from CERN and I.
LASER always has a strong practical bent, but this year it is particularly pronounced as you can see from the list of speakers and their affiliations. The topic is particularly timely: exploring the software aspects of game-changing developments currently redefining the IT scene.
The LASER formula is by now well-tuned: lectures over seven days (Sunday to Saturday), about five hours in the morning and three in the early evening, by world-class speakers; free time in the afternoon to enjoy the magnificent surroundings; 5-star accommodation and food in the best hotel of Elba, made affordable as we come towards the end of the season (and are valued long-term customers). The group picture below is from last year’s school.
Participants are from both industry and academia and have ample opportunities for interaction with the speakers, who typically attend each others’ lectures and engage in in-depth discussions. There is also time for some participant presentations; a free afternoon to discover Elba and brush up on your Napoleonic knowledge; and a boat trip on the final day.
Information about the 2013 school can be found here.
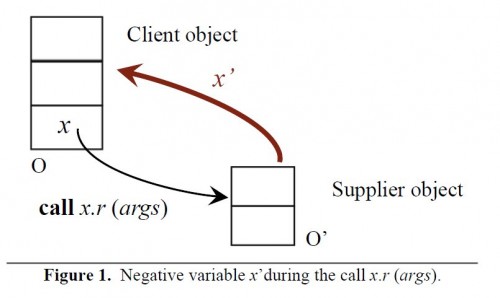
Negative variables and the essence of object-oriented programming (new paper)
In modeling object-oriented programs, for purposes of verification (proofs) or merely for a better understanding, we are faced with the unique “general relativity” property of OO programming: all the operations you write (excluding non-OO mechanisms such as static functions) are expressed relative to a “current object” which changes repeatedly during execution. More precisely at the start of a call x.r (…) and for the duration of that call the current object changes to whatever x denotes — but to determine that object we must again interpret x in the context of the previous current object. This raises a challenge for reasoning about programs; for example in a routine the notation f.some_reference, if f is a formal argument, refers to objects in the context of the calling object, and we cannot apply standard rules of substitution as in the non-OO style of handling calls.
In earlier work [1, 2] initially motivated by the development of the Alias Calculus, I introduced a notion of negative variable to deal with this issue. During the execution of a call x.r (…) the negation of x , written x’, represents a back pointer to the calling object; negative variables are characterized by axiomatic properties such as x.x’= Current and x’.(old x)= Current. Alexander Kogtenkov has implemented these ideas and refined them.
In a recent paper under submission [3], we review the concepts and applications of negative variables.
References
[1] Bertrand Meyer: Steps Towards a Theory and Calculus of Aliasing, in International Journal of Software and Informatics, 2011, available here.
[2] Bertrand Meyer: Towards a Calculus of Object Programs, in Patterns, Programming and Everything, Judith Bishop Festschrift, eds. Karin Breitman and Nigel Horspool, Springer-Verlag, 2012, pages 91-128, available here.
[3] Bertrand Meyer and Alexander Kogtenkov: Negative Variables and the Essence of Object-Oriented Programming, submitted for publication, 2012. [Updated 13 January 2014: I have removed the link to the draft mentioned in this post since it is now superseded by the new version, soon to be published, and available here.]