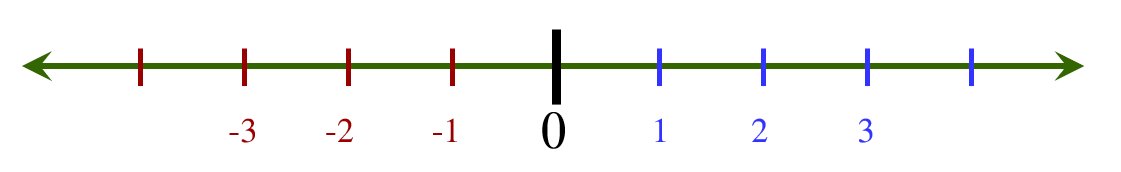This week, Informatics Europe, the association of European computer science departments and industry research centers, is holding its annual ECSS event, bizarrely billed as “20 years of Informatics Europe”. (Informatics Europe was created at the end of 2006 and incorporated officially in 2011. The first ever mention of the name appeared in an email from Jan van Leeuwen to me with cc to Christine Choppy, received on 23 October 2006 at 21:37 — we were working late. Extract from Jan’s message: “The name `Informatics Europe’ has emerged as as a name that several people find appealing (and  www.informatics-europe.org seems free).” So this year is at most the 18th anniversary.)

I would have liked to speak at this week’s event but was rejected, as explained at the end of this note. I am jotting down here a partial sketch of what I would have said, at least the introduction. (Engaging in a key-not since I was not granted a keynote.) Some of the underlying matters are of great importance and I hope to have the opportunity to talk or write about them in a more organized form in the future.

Informatics Europe came out of a need to support and unite Europe’s computer science (informatics) community. In October 2004 (funny how much seems to happen in October) Willy Zwaenepoel, chair of CS at EPFL (ETH Lausanne) wrote to me as the CS department head at ETH Zurich with an invitation to meet and discuss ways to work together towards making the discipline more visible in Switzerland. We met shortly thereafter, for a pleasant Sunday dinner on November 14. I liked his idea but suggested that any serious effort should happen at the European level rather than just Switzerland. We agreed to try to convince all the department heads that we could find across Europe and invite them to a first meeting. In the following weeks a frantic effort took place to identify, by going through university web sites and personal contacts, as many potential participants as possible. The meeting,  dubbed ECSS for European Computer Science Summit, took place at ETH Zurich on (you almost guessed it) 20-21 October 2005. The call for participation started with:

The departments of computer science at EPF Lausanne and ETH Zurich are taking the initiative of a first meeting of heads of departments in Europe.

Until now there hadn’t been any effort, comparable to the Computing Research Association in the US with its annual “Snowbird” conference, to provide a forum where they could discuss these matters and coordinate their efforts. We feel it’s time to start.

The event triggered enormous enthusiasm and in the following years we created the association (first with another name, pretty ridiculous in retrospect, but fortunately Jan van Leeuwen intervened) and developed it. For many years the associated was hosted at ETH in my group, with a fantastic Executive Board (in particular its two initial vice presidents, Jan van Leeuwen and Christine Choppy) and a single employee (worth many), Cristina Pereira, who devoted an incredible amount of energy to develop services for the members, who are not individuals but organizations (university departments and industry research labs). One of the important benefits of the early years was to bring together academics from the Eastern and Western halves of the continent, the former having still recently emerged from communism and eager to make contacts with their peers from the West.

This short reminder is just to situate Informatics Europe for those who do not know about the organization. I will talk more about it at the end because the true subject of this note is not the institution but European computer science. The common concern of the founders was to bring the community together and enable it to speak with a single voice to advance the discipline. The opening paragraphs of a paper that Zwaenepoel and I published in Communications of the ACM to announce the effort (see here for the published version, or here for a longer one, pre-copy-editing) reflect this ambition:

Europe’s contribution to computer science, going back seventy years with Turing and Zuse, is extensive and prestigious; but the European computer science community is far from having achieved the same strength and unity as its American counterpart. On 20 and 21 October 2005, at ETH Zurich, the “European Computer Science Summit” brought together, for the first time, heads of computer science departments throughout Europe and its periphery. This landmark event was a joint undertaking of the CS departments of the two branches of the Swiss Federal Institute of Technology: EPFL (Lausanne) and ETH (Zurich).

.
The initiative attracted interest far beyond its original scope. Close to 100 people attended, representing most countries of the European Union, plus Switzerland, Turkey, Ukraine, Russia, Israel, a delegate from South Africa, and a representative of the ACM,
Russ Shackelford, from the US. Eastern Europe was well represented. The program consisted of two keynotes and a number of panels and workshops on such themes as research policy, curriculum harmonization, attracting students, teaching CS to non-CS students, existing national initiatives, and plans for a Europe-wide organization. The reason our original call for participation attracted such immediate and widespread interest is that computer science in Europe faces a unique set of challenges as well as opportunities. There were dozens of emails in the style “It’s high time someone took such an initiative”; at the conference itself, the collective feeling of a major crystallizing event was palpable.

.
The challenges include some old and some new. Among the old, the fragmentation of Europe and its much treasured cultural diversity have their counterparts in the organization of the educational and research systems. To take just three examples from the education side, the UK has a system that in many ways resembles the US standard, although with significant differences (3- rather than 4-year bachelor’s degree, different hierarchy of academic personnel with fewer professors and more lecturers); German universities have for a long time relied on a long (9-semester) first degree, the “Diplom”; and France has a dual system of “Grandes Écoles”, engineering schools, some very prestigious and highly competitive, but stopping at a Master’s-level engineering degree, and universities with yet another sequence of degrees including a doctorate.

And so on. The immediate concerns in 2024 are different (Bologna adoption woes are a thing of the past) but the basic conundrum remains: the incredible amount of talent and creativity present in Europe remains dormant; research in academia (and industry) fails to deliver anywhere close to its potential. The signs are everywhere; as this note is only a sketch let me just mention a handful. The following picture  shows the provenance of papers in this year’s International Conference on Software Engineering (ICSE), the premier event in the field. Even if you cannot read all the details (it’s a photo taken quickly from a back row in the opening session, sorry for the bad quality), the basic message is unmistakable: all China, the US, then some papers from Singapore, Australia and Canada. A handful from Germany and Switzerland, not a single accepted paper from France! In a discipline that is crucial for the future of every European nation.

Venture capital? There is a bit more than twenty years ago, but it is still limited, avaricious and scared of risks. Government support? Horizon and other EU projects have helped many, with ERC grants  in particular (a brilliant European exclusive) leading to spectacular successes, but the bulk of the funding is unbelievably bureaucratic, forcing marriages of reason between institutions that have nothing in common (other than the hope of getting some monies from Brussels) and feeding a whole industry of go-between companies which claim to help applicants but contribute exactly zero to science and innovation. They have also had the perverse effect of limiting national sources of funding. (In one national research agency on whose evaluation committee I sat,  the acceptance rate is 11%. In another, where I recently was on the expert panel, it’s more like 8%. Such institutions are the main source of non-EU research funding in their respective countries.)

The result? Far less innovation than we deserve and a brain drain that every year gets worse. Some successes do occur, and we like to root for Dassault, SAP, Amadeus and more recently companies like Mistral, but almost all of the top names in technology   — like them or loathe them  — are US-based (except for their Chinese counterparts): Amazon, Microsoft, Google, OpenAI, Apple, Meta, X, or (to name another software company) Tesla. They benefit from European talent and European education: some have key research centers in Europe, and all have European engineers and researchers. So do non-European universities; not a few of  the ICSE papers labelled above as “American” or “Canadian” are actually by European authors. Talk to a brilliant young researcher or bright-eyed entrepreneur in Europe: in most cases, you will hear that he wants to find a position or create a company in the US, because that is where the action is.

Let me illustrate the situation with a vivid example. In honor of Niklaus Wirth’s 80th birthday I co-organized a conference in 2014 where at the break a few of us were chatting with one of the speakers, Vint Cerf. Someone asked him a question which was popping up everywhere at that time, right in the middle of the Snowden affair: “if you were a sysadmin for a government organization, would you buy a Huawei router?”. Cerf’s answer was remarkable: I don’t know, he said, but there is one thing I do not understand: why in the world doesn’t Europe develop its own cloud solution? So honest, coming from an American — a Vice President at Google! — and so true. So true today still: we are all putting all our data on Amazon’s AWS and Cerf’s employer’s Google Cloud and IBM Cloud and Microsoft Azure. Total madness. (A recent phenomenon that appears even worse is something I have seen happening at European university after university: relinquishing email and other fundamental solutions to Microsoft! More and more of us now have our professional emails at outlook.com. Even aside from the technical issues, such en-masse surrender is demented.) Is Europe so poor or so retarded that it cannot build local cloud or email solutions? Of course not. In fact, some of the concepts were invented here!

This inability to deliver on our science and technology potential is one of the major obstacles to social and economic improvement in Europe. (Case in point: there is an almost one-to-one correspondence between the small set of countries that are doing better economically than the rest of the Europe, often much better, and the small set of countries that take education and science seriously, giving them enough money and freeing them from overreaching bureaucracy. Did I mention Switzerland?) The brain drain should be a major source of worry; some degree of it is of course normal — enterprising people move around, and there are objective reasons for the magnetic attraction of the US — but the phenomenon is dangerously growing and is too unidirectional. Europe should offer its best and brightest a local choice commensurate with the remote one.

Many cases seem to suggest that Europe has simply given up on its ambitions. One specific example — academia-related but important — adds to the concerns raised apropos ICSE above. With a group of software engineering pioneers from across Europe (including some who would later help with Informatics Europe) we started the European Software Engineering Conference in 1987. I was the chair of the first conference, in Strasbourg that year, and the chair of the original steering committee for the following years (I later organized the 2013 session). The conference blossomed, reflecting the vibrant life of the European software engineering community, and open of course to researchers from all over the world. (The keynote speaker in Strasbourg was David Parnas, who joked that we had invited him, an American, because the French and Germans would never agree to a speaker from the other country. That quip was perhaps funny but as unfair as it was wrong: founders from different countries, notably including Italy and Belgium, even the UK, were working together in  a respectful and friendly way without any national preferences.) Having done my job I stepped aside but was flabbergasted to learn some years later that ESEC had attached itself to a US-based event, FSE (the symposium on Foundations of Software Engineering). The inevitable and predictable happened: FSE was supposed to be ESEC-FSE every other year, but soon that practice fell out and now ESEC is no more. FSE is not the culprit here: it’s an excellent conference (I had a paper in the last edition), it is just not European. My blood boils each time I think about how the people who should have nurtured and developed ESEC, the result of many years of discussions and of excellent Europe-wide cooperation, betrayed their mission and let the whole thing disappear. Pathetic and stupid, and terrible for Europe, which no longer has an international conference in this fundamental area of modern technology.

The ESEC story helps think about the inevitable question: who is responsible? Governments are not blameless; they are good at speeches but less at execution. When they do intervene, it’s often with haste (reacting to hype with pharaonic projects that burn heaps of money before running out of favor and delivering nothing). In France, the tendency is sometimes to let the state undertake technical projects that it cannot handle; the recipes that led to the TGV or Ariane do not necessarily work for IT. (A 2006 example was an attempt to create a homegrown search engine, which lasted just long enough to elicit stinging mockery in the Wall Street Journal, “Le Google”, unfortunately behind a paywall.)

It is too easy, however, to cast all the blame on outsiders. Perhaps the most important message that I would have wanted to convey to the department heads, deans, rectors and other academic decision-makers attending ECSS this week is that we should stop looking elsewhere and start working on the problems for which we are responsible. Academia is largely self-governed. Even in centralized countries where many decisions are made at the national level in ministries, the staff in those ministries largely consists of academics on secondment to the administration. European academia — except in the more successful countries, already alluded to, and by the way not exempt either from some of the problems of their neighbors — is suffocating under the weight of absurd rules. It is fashionable to complain about the bureaucracy, but many of the people complaining have the power to make and change these rules.

The absurdities are everywhere. In country A, a PhD must take exactly three years. (Oh yes? I thought it was the result that mattered.) By the way, if you have funding for 2.5 years, you cannot hire a PhD student (you say you will find the remaining funding in due time? What? You mean you are taking a risk?) In country B, you cannot be in the thesis committee of the student you supervised. (This is something bequeathed from the British system. After Brexit!) Countries C, D, E and F (with probably G, H, I, J and K to follow) have adopted the horrendous German idea of a “habilitation”, a second doctorate-like process after the doctorate, a very effective form of infantilization which maintains scientists in a subservient state until their late thirties, preventing them during their most productive years from devoting their energy to actual work. Universities everywhere subject each other to endless evaluation schemes in which no one cares about what you actually do in education and research but the game is about writing endless holier-than-thou dissertations on inclusiveness, equality etc. with no connection to any actual practice. In country L, politicized unions are represented in all the decision-making bodies and impose a political agenda, censoring important areas of research and skewing scientist hires on the basis of political preferences. In country M, there is a rule for every elementary event of academic life and the rule suffers no exception (even when you discover that it was made up two weeks earlier with the express goal of preventing you from doing something sensible). In country N, students who fail an exam have the right to a retake, and then a second retake, and then a third retake, in oral form of course. In country O, where all university presidents make constant speeches about the benefits of multidisciplinarity, a student passionate about robotics but with a degree in mechanical engineering cannot enroll in a master degree in robotics in the computer science department. In country P (and Q and R and S and T) students and instructors alike must, for any step of academic life, struggle with a poorly designed IT system, to which there is no alternative. In country U, expenses for scientific conferences are reimbursed six months later, when not rejected as non-conformant. In country V, researchers and educators are hired through a protracted  committee process which succeeds in weeding out candidates with an original profile. In country W, the primer criterion for hiring researchers is the H-index. In country X, it is the number of publications. In country Y, management looks at your research topics and forces you to change them every five years. I would need other alphabets but could go on.

When we complain about the difficulties to get things done, we are very much like the hero of Kafka’s Before the Law, who grows old waiting in front of a gate, only to learn in his final moments that he could just have entered by pushing it. We need to push the gate of European academia. No one but we ourselves is blocking it. Start by simplifying everything, but there are more ways to enter; they  are what I would have liked to present at ECSS and will have to wait for another day.

Which brings me back to the ECSS conference. I wrote to its organizers asking for the opportunity to give a talk. Naïvely, I thought the request would be obvious. After all, while Informatics Europe was at every step a group effort, with an outstanding group of colleagues from across Europe (I mentioned a few at the beginning, but there were many more, including all the members of the initial Executive Board), I played the key role as one of the two initiators of the idea, the organizer of the initial meeting and several of the following ECSS, the founding president for two terms (8 years), the prime writer of the foundational documents, the host of the first secretariat for many years in my ETH chair, the lead author of several reports, the marketer recruiting members, and the jack-of-all-trades for Informatics Europe. It may be exaggerated to say that for the first few years I carried the organization on my shoulders, but it is a fact that I found the generous funding (from ETH, industry partners and EPFL thanks to Zwaenepoel) that enabled us to get started and enabled me, when I passed the baton to my successor, to give him an organization in a sound financial situation, some 80 due-paying members, and a strong record of achievements. Is it outrageous, after two decades, to ask for a microphone to talk about the future for 45 minutes? The response I got from the Informatics Europe management was as surprising as it was boorish: in our program (they said in February 2024!) there is no place left. To add injury to insult they added that if I really wanted I could participate in some kind of panel discussion. (Sure, fly to Malta in the middle of the semester, cancel 4 classes and meetings, miss paper deadlines, all for 5 minutes of trying to put in a couple of words. By the way, one of the principles we had for the organization of ECSS was always to be in a big city with an important local community and an airport with lots of good connections to the principal places in Europe — and beyond for our US guests.) When people inherit a well-functioning organization, the result of hard work by a succession of predecessors, it is hard to imagine what pleasure they can take in telling them to go to hell. Pretty sick.

For me Informatics Europe was the application to my professional life of what remains a political passion: a passion for Europe and democracy. On this same blog in 2012 I published an article entitled “The most beautiful monument of Europe”, a vibrant hymn to the European project. While I know that some of it may appear naïve or even ridiculous, I still adhere to everything it says and I believe it is worth reading. While I have not followed the details of the activities of Informatics Europe since I stopped my direct involvement, I am saddened not to see any trace of European sentiment in it. We used to have Ukrainian members, from Odessa Polytechnic, who participated in the first ECSS meetings; today there is no member from Ukraine listed. One would  expect to see prominent words of solidarity with the country, which is defending our European values, including academic ones. Is that another sign of capitulation?

I am also surprised to see few new in-depth reports. Our friends from the US Computing Research Association, who were very helpful at the beginning of Informatics Europe (they included in particular Andy Bernat and Ed Laszowka, and Willy Zwaenepoel himself who had been a CRA officer during his years in the US), told us that one of the keys to success was to provide the community with factual information. Armed with that advice, we embarked on successive iterations of the “Informatics in Europe: Key Data” reports, largely due to the exhaustive work of Cristina Pereira, which provided unique data on salaries (something that we often do not discuss in Europe, but it is important to know how much a PhD student, postdoc, assistant professor of full professor makes in every surveyed country), student numbers, degrees, gender representation etc. etc., with the distinctive quality that — at Cristina’s insistence —we favored exactness over coverage: we included only the countries for which we could get reliable data, but for those we guaranteed full correctness and accuracy. From the Web site it seems these reports — which indeed required a lot of effort, but are they not the kind of thing the membership expects? — were discontinued some years ago. While the site shows some other interesting publications (“recommendations”), it seems regrettable to walk way from hard foundational work.

New management is entitled to its choices (as previous management is entitled to raise concerns). Beyond such differences of appreciation, the challenges facing European computer science are formidable. The enemies are outside, but they are also in ourselves. The people in charge are asleep at the wheel. I regret not to have had the opportunity to try to wake them up in person, but I do hope for a collective jolt to enable our discipline to bring Europe the informatics benefits Europe deserves.

Reading notes. From: Quelques éléments d’histoire des nombres négatifs (Elements of a history of negative numbers) by Anne Boyé, Proyecto Pénélope, 2002, revision available here; On Solving Equations, Negative Numbers, and Other Absurdities: Part II by Ralph Raimi, available  here; Note sur l’histoire des nombres entiers négatifs (Note on the History of Negative Numbers) by Rémi Lajugie, 2016, here;  The History of Negative Numbers by Leo Rogers, here; Historical Objections against the Number Line, by Albrecht Heeffer, here; Making Sense of Negative Numbers by Cecilia Kilhamn, 2011 PhD thesis at the University of Gothenburg, here.  Also the extensive book by Gert Schubring on Number Concepts Underlying the Development of Analysis in 17-19th Century France and Germany, here. Translations are mine (including from Maclaurin and De Morgan, retranslated from Lajugie’s and Boyé’s French citations). This excursion was spurred by a side remark in the article How to Take Advantage of the Blur Between the Finite and the Infinite by the recently deceased mathematician Pierre Cartier, available here.

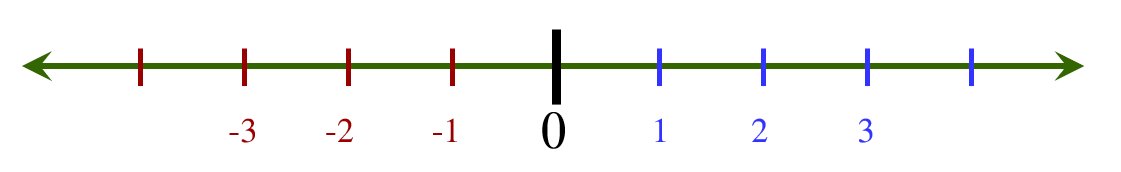
At dinner recently, with non-scientists, discussion revolved about ages and a very young child, not even able to read yet, volunteered about his forthcoming little brother that “when he comes out his age will be zero”. An adult remarked “indeed, and right now his age is minus five months”, which everyone young and old seemingly found self-evident. How remarkable!

From a elite concept to grade school topic

It is a characteristic of potent advances in human understanding that for a while they are understandable to a few geniuses only, or, if not geniuses, to a handful of forward-thinking luminaries, and a generation later, sometimes less, they are taught in grade school. When I came across object-oriented programming, those of us who had seen the light, so to speak, were very few. Feeling very much like plotting Carbonari, we would excitedly meet once in a while in exotic locations (for my Simula-fueled band usually in Scandinavia, although for the Smalltalk crowd it must have been California) to share our shared passion and commiserate about the decades it would take for the rest of humankind to see the truth. Then at some point, almost overnight, without any noticeable harbinger, the whole thing exploded and from then on it was object-oriented everything. Nowadays every beginning programmer talks objects — I did not write “understands”, they do not, but that will be for another article.

Zero too was a major invention. Its first recorded use as a number (not just a marker for absent entities) was in India in the first centuries of our era. It is not hard to imagine the mockeries. “Manish here has twenty sheep, Rahul has twelve sheep, and look at that nitwit Shankar, he sold all his sheep and still claims he has some, zero of them he says! Can you believe the absurdity? Ha ha ha.”

That dialog is imaginary, but for another momentous concept, negative numbers, we have written evidence of the resistance. From the best quarters!

The greatest minds on the attack

The great Italian mathematician Cardan (Gerolamo Cardano), in his Ars Magna from 1545, was among the skeptics. As told in a 1758 French History of Mathematics by Montucla (this quote and the next few ones are from Boyé):

In his article 7 Cardan proposes an equation which in our language would be x² + 4 x = 21 and observes that the value of x can equally be +3 or -7, and that by changing the sign of the second term it becomes -3 or +7. The name he gives to such values is “fake”.

The words I am translating here as “fake values” are, in Montucla, valeurs feintes, where feint in French means feigned, or pretended (“pretend values”). Although I have not seen the text of Ars Magna, which is in Latin anyway, I like to think that Cardan was thinking of the Italian word finto. (Used for example  in the title of an opera composed by Mozart at the age of 19, La Finta Giardinera, the fake girl gardener — English has no feminine for “gardener”. The false gardenerette in question is a disguised marchioness.) It is fun to think of negative roots as feigned.

Cardan also uses terms like “abundant” versus “failing” quantities (abondantes and défaillantes in French texts) for positive and negative:

Simple advice: do not confuse failing quantities with abundant quantities. One must add the abundant quantities between themselves, also subtract failing quantities between themselves, and subtract failing quantities from abundant quantities but only by taking species into account, that is to say, only operate same with same […]

There is a recognition of negative values, but with a lot of apprehension. Something strange, the author seems to feel, is at play here. Boyé cites the precedent of Chinese accountants who could manipulate positive values through black sticks and negative ones through red sticks and notes that it resembles what Cardan seems to be thinking here. In the fifteenth century, Nicolas Chuquet “used negative numbers as exponents but referred to them as `absurd numbers’”.

For all his precautions, Cardan did consider negative quantities. No lesser mind as Descartes, a century later (La Géométrie, 1637), is more circumspect. In discussing roots of equations he writes:

Often it turns out that some of those roots are false, or less than nothing [“moindres que rien”] as if one supposes that x can also denote the lack of a quantity, for example 5, in which case we have x + 5 = 0, which, if we multiply it by x³ − 9 x²  + 26 x − 24 = 0 yields  x⁴ − 4 x³ − 19 x² + 106 x − 120 = 0, an equation for which there are four roots, as follows: three true ones, namely 2, 3, 4, and a false one, namely 5.

Note the last value: “5”. Not a -5, but a 5 dismissed as “false”. The list of exorcising adjectives continues to grow: negative values are no longer “failing”, or “fake”, or “absurd”, now for Descartes they are “false”!  To the modern mind they are neither more nor less true than the “true” ones, but to him they are still hot potatoes, to be handled with great suspicion.

Carnot cannot take the heat

One more century later we are actually taking a step back with Lazare Carnot. Not the one of the thermodynamic cycle — that would be his son, as both were remarkable mathematicians and statesmen. Lazare in 1803 cannot hide his fear of negative numbers:

If we really were to obtain a negative quantity by itself, we would have to deduct an effective quantity from zero, that is to say, remove something from nothing : an impossible operation. How then can one conceived a negative quantity by itself?.

(Une quantité négative isolée : an isolated negative quantity, meaning a negative quantity considered in isolation). How indeed! What a scary thought!

The authors of all these statements, even when they consider negative values, cannot bring themselves to talk of negative numbers, only of negative quantities. Numbers, of course, are positive: who has ever heard of a shepherd who is guarding a herd of minus 7 lambs? Negative quantities are a slightly crazy concoction to be used only reluctantly as a kind of kludge.

Lajugie mentions another example, mental arithmetic: to compute 19 x 31  in your head, it is clever to multiply (20 -1) by (30 + 1), but then as you expand the product by applying the laws of distributivity you get negative values.

De Morgan too

We move on by three decades to England and Augustus De Morgan, yes, the one who came up with the two famous laws of logic duality. De Morgan in 1803, as cited by Raimi:

8-3 is easily understood; 3 can be taken from 8 and the remainder is 5; but 3-8 is an impossibility; it requires you to take from 3 more than there is in 3, which is absurd. If such an expression as 3-8 should be the answer to a problem, it would denote either that there was some absurdity inherent in the problem itself, or in the manner of putting it into an equation.

Raimi points out that “De Morgan is not naïve” but wants to caution students about possible errors. Maybe, but we are back to fear and to words such as “absurd”, as used by Chuquet three centuries before. De Morgan (cited by Boyé) doubles down in his reluctance to accept negatives as numbers:

0 − a is just as inconceivable as -a.

Here is an example. A father is 56 years old and his [son] is 29 years old. In how many years will the father’s age be twice his son’s age? Let x be that number of years; x satisfies 56 +x = 2 (29 + x). We find x = -2.

Great, we say, he got it! This simple result is screaming at De Morgan but he has to reject it:

This result is absurd. However if we change x into -x and correspondingly resolve 56−x = 2 (29−x), we find x = -2. The [previous] negative answer shows that we had made an error in the initial phrasing of the equation.

In other words, if you do not like the solution, change the problem! I too can remember a few exam situations in which I would have loved to make an equation more sympathetic by replacing a plus sign with a minus. Too bad no one told me I could.

De Morgan’s comment is remarkable as the “phrasing of  the equation” contained no “error” whatsoever.   The equation correctly reflected the problem as posed. One could find the statement of the problem mischievous (“in how many years” suggests a solution in the future whereas there is only one in the past), but the equation is meaningful and  has a solution — one, however, that horrifies De Morgan. As a result, when discussing the quadratic (second-degree) equation ax² + bx + c = 0, instead of accepting that a, b and c can be negative, he distinguishes no fewer than 6 cases, such as ax² – bx + c = 0, ax² + bx – c = 0 etc. The coefficients are always non-negative, it is the operators that change between + and  -. As a consequence, the determinant actually has two possible values, the one familiar to us, b² – 4ac, but also b² + 4ac for some of the cases. According to Raimi, many American textbooks of the 19th century taught that approach, forcing students to remember all six cases. (For a report about a current teaching distortion of the same topic, see a recent article on the present blog, “Mathematics Is Not a Game of Hit and Miss”, here.)

De Morgan (cited here by Boyé) feels the need to turn this reluctance to use negative numbers into a general rule:

When the answer to a problem is negative, by changing the sign of x in the equation that produced the result, we can discover that an error was made in the method that served to form this equation, or show that the question asked by the problem is too limited.

Sure! It is no longer “if the facts do not fit the theory, change the facts” (a sarcastic definition of bad science), but also “if you do not like the solution, change the problem”. All the more unnecessary (to a modern reader, who thanks to the work of countless mathematicians over centuries learned negative numbers in grade school, and does not spend time wondering whether they mean something) that if we keep the original problem the computed solution, x = -2, makes perfect sense: the father was twice his son’s age two years ago. The past is a negative future. But to see things this way, and to accept that there is nothing fishy here, requires a mindset for which an early 19-th century mathematician was obviously not ready.

And Pascal, and Maclaurin

Not just a mathematician but a great mathematical innovator. What is remarkable in all such statements against negative numbers is that they do not emanate from little minds, unable to grasp abstractions. Quite the contrary! These negative-number-skeptics are outstanding mathematicians. Lajugie gives more examples from the very top. Blaise Pascal in 1670:

Too much truth surprises; I know people who cannot understand that when you deduct 4 from zero, what remains is zero.

(Oh yes?, one is tempted to tell the originator of probability theory, who was fascinated by betting and games of chance: then I put the 4 back and get 4? Quick way to get rich. Give me the address of that casino please.) A friend of Pascal, skeptical about the equality -1 / 1 = 1 / -1: “How could a smaller number be to a larger one as a larger one to a smaller one?”. An English contemporary, John Wallis, one of the creators of infinitesimal calculus — again, not a nitwit! — complains that a / 0 is infinity, but since in a / -1 the denominator is lesser than zero it must follow that a / -1, which is less than zero (since it is negative by the rule of signs), must also be greater than infinity! Nice one actually.

This apparent paradox also bothered the great scientist D’Alembert, the 18-th century co-editor of the Encyclopédie, who resolves it, so to speak, by stating (as cited by Heeffer) that “One can only go from positive to negative through either zero or through infinity”; so unlike Wallis he accepts that 1 / -a is negative, but only because it becomes negative when it passes through infinity. D’Alembert concludes (I am again going after Heeffer) that it is wrong to say that negative numbers are always smaller than zero. Euler was similarly bothered and similarly looking for explanations through infinity: what does Leibniz’s expansion of 1 / (1 – x)  into 1 + x + x² + x³ + … become for x = 2? Well, the sum 1 + 2 + 4 + 8 + … diverges, so 1 / -1 is infinity!

We all know the name “Maclaurin” from the eponymous series. Colin Maclaurin  wrote in 1742, decades after Pascal (Boyé):

The use of the negative sign in algebra leads to several consequences that one initially has trouble accepting and has led to ideas that seem not to have any real foundation.

Again the supposed trouble is the absence of an immediately visible connection to everyday reality (a “real foundation”). And again Maclaurin accepts that quantities can be negative, but numbers cannot:

While abstract quantities can be both negative and positive, concrete quantities are not always capable of being the opposite of each other.

(cited by Kilhamn). Apparently Colin’s wife Anne never thought of buying him a Réaumur thermometer (see below) for his birthday.

Yes, two negatives make a positive

We may note that the authors cited above, and many of their contemporaries, had no issue manipulating negative quantities in some contexts, and to accept the law of signs, brilliantly expressed by the Indian mathematician Brahmagupta  in the early 7th century (not a typo); as cited by Rogers:

A debt minus zero is a debt.

A fortune minus zero is a fortune.

Zero minus zero is a zero.

A debt subtracted from zero is a fortune.

A fortune subtracted from zero is a debt.

The product of zero multiplied by a debt or fortune is zero.

The product of zero multiplied by zero is zero.

The product or quotient of two fortunes is one fortune.

The product or quotient of two debts is one fortune.

The product or quotient of a debt and a fortune is a debt.

The product or quotient of a fortune and a debt is a debt.

That view must have been clear to accountants. Whatever Pascal may have thought, 4 francs removed from nothing do not vanish; they become a debt. What the great mathematicians cited above could not fathom was that there is such a thing as a negative number. You can count up as far as your patience will let you; you can then count down, but you will inevitably stop. Everyone knows that, and even Pascal or Euler have trouble going beyond. (Old mathematical joke: “Do you know about the mathematician who was afraid of negative numbers? He will stop at nothing to avoid them”.)

The conceptual jump that took centuries to achieve was to accept that there are not only negative quantities, but negative numbers: numbers in their own right, not just temporarily  negated positive numbers (that is, the only ones to which we commonly rely in everyday life), prefaced with a minus sign because we want to use them as “debts”, but with the firm intention to move them back to the other side so as to restore their positivity  — their supposed naturalness —  at the end of the computation. We have seen superior minds “stopping at nothing” to avoid that step.

Others were bolder; Schubring has a long presentation of how Fontenelle, an 18-th century French scientist and philosopher who contributed to many fields of knowledge,  made the leap.

Not everyone may yet get it

While I implied above that today even small children understand the concept, we may note in passing that there may still be people for whom it remains a challenge. Lajugie notes that the Fahrenheit temperature scale frees people from having to think about negative temperatures in ordinary circumstances, but since the 18-th century the (much more reasonable) Réaumur thermometer and Celsius scale goes under as well as above zero, helping people get familiar with negative values as something quite normal and not scary. (Will the US ever switch?)

Maybe the battle is not entirely won.  Thanks to Rogers I learned about the 2018 Lottery Incident in the United Kingdom of Great Britain and Northern Ireland, where players could win by scratching away, on a card, a temperature lower than the displayed figure. Some temperatures were below freezing. The game had to be pulled after less than a week as a result of player confusion. Example complaints included this one from a  23-year-old who was adamant she should have won:

“On one of my cards it said I had to find temperatures lower than -8. The numbers I uncovered were -6 and -7 so I thought I had won, and so did the woman in the shop. But when she scanned the card the machine said I hadn’t. I phoned Camelot [the lottery office] and they fobbed me off with some story that -6 is higher – not lower – than -8 but I’m not having it. I think Camelot are giving people the wrong impression – the card doesn’t say to look for a colder or warmer temperature, it says to look for a higher or lower number. Six is a lower number than 8. Imagine how many people have been misled.“

Again, quantities versus numbers. As we have seen, she could claim solid precedent for this reasoning. Most people, of course, have figured out that while 8 is greater than 6 (actually, because of that), -6 is greater than -8. But as Lajugie points out the modern, rigorous definition of negative numbers is (in the standard approach) far from the physical intuition (which typically looks like the two-directional line pictured at the beginning of this article, with numbers spreading away from zero towards both the right and the left). The picture helps, but it is only a picture.

Away from the perceptible world

If we ignore the intuition coming from observing a Réaumur or Celsius thermometer (which does provide a “real world” guide), the early deniers of negative numbers were right that this concept does not directly reflect the experiential understanding of numbers, readily accessible to everyone. The general progress of science, however, has involved moving away from such immediate intuition. Everyday adventures (such as falling on the floor) absolutely do not suggest to us that matter is made of sparse atoms interacting through electrical and magnetic phenomena. This march towards abstraction has guided the evolution of modern science — most strikingly, the evolution of modern mathematics.

Some lament this trend; think of the negative reactions to the so-called “new math”. (Not from me. I was caught by the  breaking of the wave and loved every minute of it.) But there is no going back; in addition, it is well known that some of the initially most abstract mathematical development, initially pursued without any perceived connection with reality, found momentous unexpected applications later on; two famous examples are Minkowski’s space-time formalism, which provided the mathematical framework for specifying relativity, and number-theoretical research about factoring large numbers into primes, which made modern cryptography (and hence e-commerce) possible.

Negative numbers too required abstraction to acquire mathematical activity. That step required setting aside the appeal to intuition and considering the purely concepts solely through its posited properties. We computer scientists would say “applying the abstract data type approach”. The switch took place sometime in the middle of the 19th century, spurred among others by Évariste Galois. The German mathematician Hermann Hankel — who lived only a little longer than Galois — explained clearly how this transition occurred for negative numbers (cited by Boyé among others):

The [concept of] number is no longer today a thing, a substance that is supposed to exist outside of the thinking subject or the objects that lead to it being considered; it is no longer an independent principle, as the Pythagoreans thought. […] The mathematician considers as impossible only that which is logically impossible, in the sense of implying a contradiction. […] But if the numbers under study are logically possible, if the underlying concept is defined clearly and distinctly, the question can no longer be whether a substrate exists in the world of reality.

A very modern view: if you can dream it, and you can make it free of contradiction (well, Hankel lived in the blissful times before Gödel), then you can consider it exists. An engineer might replace the second of these conditions by: if you can build it. And a software engineer, by: if you can compile and run it. In the end it is all the same idea.

Formally: a general integer is an equivalence class

In modern mathematics, while no one forbids you from clinging for help to some concrete intuition such as the Celsius scale, it is not part of the definition. Negative numbers are formally defined members of the zoo.

For those interested (and not remembering the details), the rigorous definition goes like this. We start from zero-or-positive integers (the set N of “natural” numbers) and consider pairs [a, b] of numbers (as we would do to define rationals, but the sequel quickly diverges). We define an equivalence relation which holds with another pair [a’, b’] if a + b’ = a’ + b. Then we can define the set Z of all integers (positive, zero, negative) as the quotient of N x N by that relation. The intuition if that the characteristic property of an equivalence class, such as [1, 4], [2, 5],  [3, 6]… , is that b – a, the difference between the second and first values, is the same for all pairs: 3 in this example (4 – 1, 5 – 2, 6 – 3 etc.). At least that property holds for b >= a; since we are starting from N, subtraction is defined only in that case. But then if we take that quotient as the definition of Z, we call members of that set “negative”, by pure convention, whenever b < a (if this property holds for one of the pairs in an equivalence class it holds for all of them), and positive if b > a. Zero is obtained for a = b.

We reestablish the connection with our good old natural integers by identifying N with the subset of Z for which b >= a. (This is an informal statement; the correct technical phrasing is that there is a “bijection” — a one-to-one correspondence, in fact an isomorphism — between that subset and N.) So we have plunged, or “embedded”, N into something bigger, to which most of its treasured properties (associativity and commutativity of addition etc.) immediately spread, while some limitations disappear; in particular, unlike in N, we can now subtract any Z integer from any other.

We also get the opposites of numbers as a result: for any m in Z, we can easily prove that there is another one n such that m + n = 0. That n can be written -m. The property is true for both positive and negative numbers, concepts that are also easy to define: we show that “>” is one of those operations that extend from N to Z, and the positive numbers are those m such that m > 0. Then if m is positive -m is negative, and conversely; 0 is the only number for which m = -m.

Remarkably, Z too is in one-to-one correspondence with N. (It is one of the definitions of an infinite set that it can be in one-to-one correspondence with one of its strict subsets, something that is obviously not possible for a finite set. To shine in cocktail parties you can refer to this property as “Dedekind-infinite”.) In other words, we have uncovered yet a new attraction of Hilbert’s Grand Hotel: the hotel has an annex, ready for the case of a guest coming with an unannounced companion. The companion will be hosted in the annex, in a room uniquely paired with the original guest’s room. The annex is a second hotel, but it is not exactly like the first: it does not have an annex of its own in the form of yet another hotel. It does have an annex, but that is the original hotel (the hotel of which it itself is the annex).

If you were not aware of the construction through equivalence classes of pairs and your reaction is “so much ado about so little! I do not need any of this to understand negative numbers and to know that m + -m = 0”, well, maybe, but you are missing part of the story: the observation that even the “natural” numbers are not that natural. Those we can readily apprehend as part of “natural” reality are the ones from 1 to something like 1000,  denoting quantities that we can reasonably count. If you really have extraordinary patience and time make this 1000,000 or even 1 million, that does not change the argument.

Even zero, as noted, took millennia to be recognized as a number. Beyond the numbers that we can readily fathom in relation to our experience at human scale, the set of natural integers is also an intellectual fiction. (Its official construction in the modern mathematical canon is seemingly even more contorted than the extension to Z sketched above: N, in the so-called Zermelo-Fraenkel theory (more pickup lines for cocktail parties!) contains the empty set for 0, and then sets each containing the previous one and a set made of that previous one. It is clearer with symbols: ø, {ø}, {ø, {ø}}, {ø, {ø}, {ø, {ø}}}, ….)

Coming back to negative numbers, Riemann (1861, cited by Schubring) held their construction as a fundamental step in the generalization process that characterizes mathematics, beautifully explaining the process:

The original object of mathematics is the integer number; the field of study increases only gradually. This extension does not happen arbitrarily, however; it is always motivated by the fact that the initially restricted view leads toward a need for such an extension. Thus the task of subtraction requires us to seek such quantities, or to extend our concept of quantity in such a way that its execution is always possible, thus guiding us to the concept of the negative.

Nature and nurture

The generalization process is also a process of abstraction. The move away from the “natural” and “intuitive” is inevitable to understand negative numbers. All the misunderstandings and fears by great minds, reviewed above, were precisely caused by an exaggerated, desperate attempt to cling to supposedly natural concepts. And we only talked about negative numbers! Similar or worse resistance met the introduction of imaginary and complex numbers (the names themselves reflect the trepidation!), quaternions and other fruitful but artificial creation of mathematics. Millenia before, the Greeks experienced shock when they realized that numbers such as π and the square root of 2 could not be expressed as ratios of integers.

Innovation occurs when someone sets out to disprove a statement of impossibility. (This technique also lies behind one approach to solving puzzles and riddles: you despair that there is no way out; then try to prove that there is no solution. Failing to complete that proof might end up opening for you the path to one.)

Parallels exist between innovators and children. Children do not know yet that some things are impossible; they make up ways. Right now I am sitting next to the Rhine and I would gladly take a short walk on the other bank, but I do not want to go all the way to the bridge and back. If I were 4 years old, I would dream up some magic carpet or other fancy device, inferred from bedtime stories, that would instantly transport me there. We grow up and learn that there are no magic carpets, but true innovators who see an unsolved problem refuse to accept that state of affairs.

In their games, children often use the conditional: “I would be a princess, and you would be a magician!”. Innovators do this too when they refuse to be stopped by conventional-wisdom statements of impossibility. They set out to disprove the statements. The French expression “prouver le mouvement en marchant”, prove movement by walking, refers to the Greek philosophers Diogenes of Sinope and  Zeno of Elea. Zeno, the story goes, used the paradox of Achilles and the tortoise to claim he had proved that movement is impossible. Diogenes proved the reverse by starting to walk.

In mathematics and in computer science, we are even more like children because we can in fact summon our magic carpets — build anything we dream of, provided we can define it properly. Mathematics and computer science are among the best illustrations of Yuval Noah Harari’s thesis that a defining characteristic of the human race is our ability to tell ourselves stories, including very large and complex stories. A mathematical theory is a story that we tell ourselves and to which we can convert other mathematicians (plus, if the theory is really successful, generations of future students). Computer programs are the same with the somewhat lateral extra condition that we must also enable some computing system to execute it, although that system is itself a powerful story that has undergone the same process. You can find variants of these observations in such famous pronouncements as Butler Lampson’s “in computer science, we can solve any problem by introducing an extra level of indirection” and Alan Kay‘s  “the best way to predict the future is to invent it”.

There is a difference, however, with children’s role-playing; and it can have dramatic effects. Children can indulge in make-believe for quite some time, continuing to live their illusions until they grow up and become reasonable. Normally they will not experience bad consequences (well, apart from the child who believes a little too hard, or from a window little too high, that his arms really are wings.) In adult innovation, sooner or later you have to reconcile the products of your imagination with the world. It may be the physical world (your autonomous robot was fantastic in the lab but it requires heavy batteries making it impractical), but things are just as bad with the virtual world of mathematics or software. It is great to define and extend your own freaky artificial worlds, but at some point you have to make sure they are consistent not just with already defined worlds but with themselves. As noted earlier, a mathematical concoction, however audacious, should be free of contradictions; and a software concept, however powerful, should be implementable. (Efficiently implementable.)

By any measure the most breathtaking virtual construction of modern mathematics is Cantor’s set theory, which scared many mathematicians,  the way negative numbers had terrified their predecessors. (Case in point: the editor of a journal to which Cantor had submitted a paper wrote that it was “a hundred years too soon”.  Cantor did not want to wait until 1984. The great mathematician Kronecker described him as “a corrupter of youth”. And so on.) More enlightened colleagues, however, soon recognized the work as ushering in a new era. Hilbert, in particular, was a great supporter, as were many of the top names in several countries. Then intellectual disaster struck.

Cantor himself and others, most famously Russell in a remark included in a letter of Frege, noticed a problem. If sets can contain other sets, and even contain themselves (the set of infinite sets must be infinite), what do we make of the set of all sets that do not contain themselves? Variants of this simple question so shook the mathematical edifice that it took a half-century to put things back in order.

Dream, check, build

Cantor, for his part, went into depression and illness. He died destitute and desperate. There may not have been a direct cause-to-effect relationship, but certainly the intellectual rejection and crisis did not help.

All the sadder that in the end set theory, after significant cleanup, turned out to be one of the biggest successes of history. We still discuss the paradoxes, but it is unlikely that today they prevent anyone from sleeping soundly at night.

Unlike those genuinely disturbing paradoxes of set theory, the paradoxes that led mathematicians of previous centuries to reject negative numbers were apparent only. They were not paradoxes but tokens of intellectual timidity.

The sole reason for fearing and skirting negative numbers was an inability to accept a construction that contradicted a simplistic view of physical reality. Like object-oriented programming and many other bold advances, all that was required was the audacity to take imagined abstractions seriously.

Dream it; check it; build it.

Recently I prepared some of my books for free access on the Web (after gaining agreement from the publishers). Here are the corresponding links. They actually point to pages that present the respective books and have further links to the actual PDF versions.

Although the texts are essentially those of the books as published, I was able in most cases to make some improvements, in particular to the formatting, and to introduce some hyperlinking, for example in table of contents, to facilitate online navigation.

If you cite any of these books please use the links given here. Then you know that you are referring your readers to a legal and up-to-date version. In particular, there are a plethora of pirated copies of Object-Oriented Software Construction on various sites, with bad formatting, no copyright acknowledgment, and none of the improvements.   academia.edu hosts one of them, downloadable. I wrote to them and they did not even answer.

Here are the books and the links.

• Introduction to the Theory of Programming Languages (Prentice Hall, 1990):  A general introduction to formal reasoning about programs and programming languages. Written without a heavy formal baggage so as to be understandable by programmers who do not have a special mathematical background. Full text freely available from here.
• Object Success (Prentice Hall, 1995): . A general presentation of object technology, meant in particular for managers and decision-makers, presenting the essential OO ideas and their effect on project management and corporate culture. Full text freely available from here.
• Object-Oriented Software Construction, 2nd edition (Prentice Hall, 1997): . The best-known of my books, providing an extensive (and long!) presentation of object technology, with particular emphasis on software engineering aspects, including Design by Contract. Introduced many ideas including some of the now classic design patterns (Command, called “undo-redo”, Bridge, called “handle” etc. Full text freely available from here.

In addition, let me include links to recent books published by Springer; they are not freely available, but many people can gain free access through their institutions:

• Touch of Class: An Introduction to Programming Well Using Objects and Contracts. My introductory programming textbook, used in particular for many years for the intro programming course, altogether to something like 6000 students over 14 years, at ETH Zurich (and nourished by experience). The Springer page with  the text (paywall) is here. There is also my own freely accessible book page with substantial extracts (read for example the chapter on recursion): here.
• Agile! The Good, the Hype and the Ugly A widely used presentation of agile methods, serving both as tutorial and as critique. The Springer page with  the text (paywall) is here. There is also my own freely accessible book page with substantial extracts: here.
• Handbook of Requirements and Business Analysis (Springer, 2022). A short but extensive textbook on requirements engineering. The Springer page with  the text (paywall) is here. My own book page, which will soon have substantial extracts and supplementary material, is here.

Also note the volume which I recently edited, The French School of Programming, Springer, 2024, with 13 chapters by top French computer scientists (and a chapter by me). The Springer page  is here.

My full list of books is here. Full publication list in chronological order: here.

I do not have a crystal ball and disaster may still strike. A terrorist attack, disruption by the hateful scoundrels of the extreme left. (Meaning I would have to eat the words below, since they will be here for the record, but then we will have worse things to deplore.)

After initial doubts I have had an increasingly good feeling, as we got closer to the event, about the Olympic games. A few months ago I feared that unions would stage irresponsible strikes, but that does not seem to be happening; if peace was bought it was worth it.

It looks like the organization has been truly efficient and professional, with the right dose of controlled craziness (for the opening ceremony). After all, for the first time in decades France has had a competent government since 2017, still in place even if on the way out, and it shows.

What if everything went according to plan and beyond expectations? What if the unimaginable just happened now?

A skillfully orchestrated production, national unity even if temporary, smiles and welcomes — two weeks of bliss?

It is permitted to hold one’s breath and cross one’s fingers.

Bienvenue à Paris.

July 14 (still here for 15 minutes) is not a bad opportunity to announced the publication of a new book: The French School of Programming.

The book is a collection of chapters, thirteen of them, by rock stars of programming and software engineering research (plus me), preceded by a Foreword by Jim Woodcock and a Preface by me. The chapters are all by a single author, reflecting the importance that the authors attached to the project. Split into four sections after chapter 1, the chapters are, in order:

1. The French School of Programming: A Personal View, by Gérard Berry (serving as a general presentation of the subsequent chapters).

Part I: Software Engineering

2. “Testing Can Be Formal Too”: 30 Years Later, by  Marie-Claude Gaudel

3. A Short Visit to Distributed Computing Where Simplicity Is Considered a First-Class Property, by Michel Raynal

4. Modeling: From CASE Tools to SLE and Machine Learning, by Jean-Marc Jézéquel

5. At the Confluence of Software Engineering and Human-Computer Interaction: A Personal Account,  by Joëlle Coutaz

Part II:  Programming Language Mechanisms and Type Systems

6. From Procedures, Objects, Actors, Components, Services, to Agents, by  Jean-Pierre Briot

7. Semantics and Syntax, Between Computer Science and Mathematics, by Pierre-Louis Curien

8. Some Remarks About Dependent Type Theory, by Thierry Coquand

Part III: Theory

9. A Personal Historical Perspective on Abstract Interpretation, by Patrick Cousot

10. Tracking Redexes in the Lambda Calculus, by  Jean-Jacques Lévy

11. Confluence of Terminating Rewriting Computations, by  Jean-Pierre Jouannaud

Part IV: Language Design and Programming Methodology

12. Programming with Union, Intersection, and Negation Types, by Giuseppe Castagna

13, Right and Wrong: Ten Choices in Language Design, by Bertrand Meyer

What is the “French School of Programming”? As discussed in the Preface (although Jim Woodcock’s Foreword does not entirely agree) it is not anything defined in a formal sense, as the variety of approaches covered in the book amply demonstrates. What could be more different (for example) than Coq, OCaml (extensively referenced by several chapters) and Eiffel? Beyond the differences, however, there is a certain je ne sais quoi of commonality; to some extent, in fact, je sais quoi: reliance on mathematical principles, a constant quest for simplicity, a taste for elegance. It will be for the readers to judge.

Being single authors of their chapters, the authors felt free to share some of their deepest insights an thoughts. See for example Thierry Coquand’s discussion of the concepts that led to the widely successful Coq proof system, Marie-Claude Gaudel’s new look at her seminal testing work of 30 years ago, and Patrick Cousot’s detailed recounting of the intellectual path that led him and Radhia to invent abstract interpretation.

The French School of Programming
Edited by Bertrand Meyer
Springer, 2024. xxiv + 439 pages

Book page on Springer site
Amazon US page
Amazon France page
Amazon Germany page

The book is expensive (I tried hard to do something about it, and failed). But many readers should be able to download it, or individual chapters, for free through their institutions.

It was a privilege for me to take this project to completion and work with such extraordinary authors who produced such a collection of gems.

The CF-Index, or Conference Frustration index, is an integer n (n ≥ 1) defined as follows. You are at a conference where your paper submission was rejected, and sitting in the session devoted to that paper’s very topic. You think for yourself  “My paper was at least n times better than the average here”. That n is your CF-index.

It is a law of nature (like speed never exceeding that of light, or temperature never going below absolute zero) that n < 1 is impossible. (The reason is obvious: if you were not the kind to believe your work is at least as good as anyone else’s, you would have gone for another profession, one calling for modesty, realism and timidity — such as, say, politician.)  Values of n = 3 or 4 are normal. Beyond 10 you might consider seeking professional advice. (These observations have nothing to do with my being at ICSE right now.)

On 13-15 September 1999 a symposium took place in St Catherine College in Oxford,  in honor of Tony Hoare’s “retirement” from Oxford (the word is in quotes because he has had several further productive careers since). The organizers were Jim Woodcock, Bill Roscoe and Jim Davies. The proceedings are available as Millenial Perspectives in Computer Science, MacMillan Education UK, edited by Davies, Roscoe and Woodcock. The Symposium was a milestone event.

As part of a recent conversation on something else, YuQian Zhou(who was also there) sent me a group photo from the event, which I did not know even existed. I am including it below; it is actually a photo of a paper photo but the resolution is good. It is a fascinating gallery of outstanding people in programming and verification. (How many Turing award winners can you spot? I see 7.)

Many thanks to YuQian Zhou, Jim Woodcock and Bill Roscoe for insights into the picture in discussions of the past two weeks.

[This is a verbatim copy of a post in the Communications of the ACM blog, 9 January 2024.]

I am still in shock from the unexpected death of Niklaus Wirth eight days ago. If you allow a personal note (not the last one in this article): January 11, two days from now, was inscribed in my mind as the date of the next time he was coming to my home for dinner. Now it is the date set for his funeral.

Niklaus Wirth at the ACM Turing centenary celebration
San Francisco, 16 June 2012
(all photographs in this article are by B. Meyer)

A more composed person would wait before jotting down thoughts about Wirth’s contributions but I feel I should do it right now, even at the risk of being biased by fresh emotions.

Maybe I should first say why I have found myself, involuntarily, writing obituaries of computer scientists: Kristen Nygaard and Ole-Johan Dahl, Andrey Ershov, Jean Ichbiah, Watts Humphrey, John McCarthy, and most recently Barry Boehm (the last three in this very blog). You can find the list with comments and links to the eulogy texts on the corresponding section of my publication page. The reason is simple: I have had the privilege of frequenting giants of the discipline, tempered by the sadness of seeing some of them go away. (Fortunately many others are still around and kicking!) Such a circumstance is almost unbelievable: imagine someone who, as a student and young professional, discovered the works of Galileo, Descartes, Newton, Ampère, Faraday, Einstein, Planck and so on, devouring their writings and admiring their insights — and later on in his career got to meet all his heroes and conduct long conversations with them, for example in week-long workshops, or driving from a village deep in Bavaria (Marktoberdorf) to Munich airport. Not possible for a physicist, of course, but exactly the computer science equivalent of what happened to me. It was possible for someone of my generation to get to know some of the giants in the field, the founding fathers and mothers. In my case they included some of the heroes of programming languages and programming methodology (Wirth, Hoare, Dijkstra, Liskov, Parnas, McCarthy, Dahl, Nygaard, Knuth, Floyd, Gries, …) whom I idolized as a student without every dreaming that I would one day meet them. It is natural then to should share some of my appreciation for them.

My obituaries are neither formal, nor complete, nor objective; they are colored by my own experience and views. Perhaps you object to an author inserting himself into an obituary; if so, I sympathize, but then you should probably skip this article and its companions and go instead to Wikipedia and official biographies. (In the same vein, spurred at some point by Paul Halmos’s photographic record of mathematicians, I started my own picture gallery. I haven’t updated it recently, and the formatting shows the limits of my JavaScript skills, but it does provide some fresh, spontaneous and authentic snapshots of famous people and a few less famous but no less interesting ones. You can find it here. The pictures of Wirth accompanying this article are taken from it.)

Niklaus Wirth, Barbara Liskov, Donald Knuth
(ETH Zurich, 2005, on the occasion of conferring honorary doctorates to Liskov and Knuth)

A peculiarity of my knowledge of Wirth is that unlike his actual collaborators, who are better qualified to talk about his years of full activity, I never met him during that time. I was keenly aware of his work, avidly getting hold of anything he published, but from a distance. I only got to know him personally after his retirement from ETH Zurich (not surprisingly, since I joined ETH because of that retirement). In the more than twenty years that followed I learned immeasurably from conversations with him. He helped me in many ways to settle into the world of ETH, without ever imposing or interfering.

I also had the privilege of organizing in 2014, together with his longtime colleague Walter Gander, a symposium in honor of his 80th birthday, which featured a roster of prestigious speakers including some of the most famous of his former students (Martin Oderski, Clemens Szyperski, Michael Franz…) as well as Vint Cerf. Like all participants in this memorable event (see here for the program, slides, videos, pictures…) I learned more about his intellectual rigor and dedication, his passion for doing things right, and his fascinating personality.

Some of his distinctive qualities are embodied in a book published on the occasion of an earlier event, School of Niklaus Wirth: The Art of Simplicity (put together by his close collaborator Jürg Gutknecht together with Laszlo Boszormenyi and Gustav Pomberger; see the Amazon page). The book, with its stunning white cover, is itself a model of beautiful design achieved through simplicity. It contains numerous reports and testimonials from his former students and colleagues about the various epochs of Wirth’s work.

Niklaus Wirth (right)
with F.L. Bauer, one of the founders of German computer science
Zurich,22 June 2005

Various epochs and many different topics. Like a Renaissance man, or one of those 18-th century “philosophers” who knew no discipline boundaries, Wirth straddled many subjects. It was in particular still possible (and perhaps necessary) in his generation to pay attention to both hardware and software. Wirth is most remembered for his software work but he was also a hardware builder. The influence of his PhD supervisor, computer design pioneer and UC Berkeley professor Harry Huskey, certainly played a role.

Stirred by the discovery of a new world through two sabbaticals at Xerox PARC (Palo Alto Research Center, the mother lode of invention for many of today’s computer techniques) but unable to bring the innovative Xerox machines to Europe, Wirth developed his own modern workstations, Ceres and Lilith. (Apart from the Xerox stays, Wirth spent significant time in the US and Canada: University of Laval for his master degree, UC Berkeley for his PhD, then Stanford, but only as an assistant professor, which turned out to be Switzerland’s and ETH’s gain, as he returned in 1968,)

Lilith workstation and its mouse
(Public display in the CAB computer science building at ETH Zurich)

One of the Xerox contributions was the generalized use of the mouse (the invention of Doug Englebart at the nearby SRI, then the Stanford Research Institute). Wirth immediately seized on the idea and helped found the Logitech company, which soon became, and remains today, a world leader in mouse technology.
Wirth returned to hardware-software codesign late in his career, in his last years at ETH and beyond, to work on self-driving model helicopters (one might say to big drones) with a Strong-ARM-based hardware core. He was fascinated by the goal of maintaining stability, a challenge involving physics, mechanical engineering, electronic engineering in addition to software engineering.
These developments showed that Wirth was as talented as an electronics engineer and designer as he was in software. He retained his interest in hardware throughout his career; one of his maxims was indeed that the field remains driven by hardware advances, which make software progress possible. For all my pride as a software guy, I must admit that he was largely right: object-oriented programming, for example, became realistic once we had faster machines and more memory.

Software is of course what brought him the most fame. I struggle not to forget any key element of his list of major contributions. (I will come back to this article when emotions abate, and will add a proper bibliography of the corresponding Wirth publications.) He showed that it was possible to bring order to the world of machine-level programming through his introduction of the PL/360 structured assembly language for the IBM 360 architecture. He explained top-down design (“stepwise refinement“), as no one had done before, in a beautiful article that forever made the eight-queens problem famous. While David Gries had in his milestone book Compiler Construction for Digital Computers established compiler design as a systematic discipline, Wirth showed that compilers could be built simply and elegantly through recursive descent. That approach had a strong influence on language design, as will be discussed below in relation to Pascal.

The emphasis simplicity and elegance carried over to his book on compiler construction. Another book with the stunning title Algorithms + Data Structures = Programs presented a clear and readable compendium of programming and algorithmic wisdom, collecting the essentials of what was known at the time.

And then, of course, the programming languages. Wirth’s name will forever remained tied to Pascal, a worldwide success thanks in particular to its early implementations (UCSD Pascal, as well as Borland Pascal by his former student Philippe Kahn) on microcomputers, a market that was exploding at just that time. Pascal’s dazzling spread was also helped by another of Wirth’s trademark concise and clear texts, the Pascal User Manual and Report, written with Kathleen Jensen. Another key component of Pascal’s success was the implementation technique, using a specially designed intermediate language, P-Code, the ancestor of today’s virtual machines. Back then the diversity of hardware architectures was a major obstacle to the spread of any programming language; Wirth’s ETH compiler produced P-Code, enabling anyone to port Pascal to a new computer type by writing a translator from P-Code to the appropriate machine code, a relatively simple task.

Here I have a confession to make: other than the clear and simple keyword-based syntax, I never liked Pascal much. I even have a snide comment in my PhD thesis about Pascal being as small, tidy and exciting as a Swiss chalet. In some respects, cheekiness aside, I was wrong, in the sense that the limitations and exclusions of the language design were precisely what made compact implementations possible and widely successful. But the deeper reason for my lack of enthusiasm was that I had fallen in love with earlier designs from Wirth himself, who for several years, pre-Pascal, had been regularly churning out new language proposals, some academic, some (like PL/360) practical. One of the academic designs I liked was Euler, but I was particularly keen about Algol W, an extension and simplification of Algol 60 (designed by Wirth with the collaboration of Tony Hoare, and implemented in PL/360). I got to know it as a student at Stanford, which used it to teach programming. Algol W was a model of clarity and elegance. It is through Algol W that I started to understand what programming really is about; it had the right combination of freedom and limits. To me, Pascal, with all its strictures, was a step backward. As an Algol W devotee, I felt let down.
Algol W played, or more precisely almost played, a historical role. Once the world realized that Algol 60, a breakthrough in language design, was too ethereal to achieve practical success, experts started to work on a replacement. Wirth proposed Algol W, which the relevant committee at IFIP (International Federation for Information Processing) rejected in favor of a competing proposal by a group headed by the Dutch computer scientist (and somewhat unrequited Ph.D. supervisor of Edsger Dijkstra) Aad van Wijngaarden.

Wirth recognized Algol 68 for what it was, a catastrophe. (An example of how misguided the design was: Algol 68 promoted the concept of orthogonality, roughly stating that any two language mechanisms could be combined. Very elegant in principle, and perhaps appealing to some mathematicians, but suicidal: to make everything work with everything, you have to complicate the compiler to unbelievable extremes, whereas many of these combinations are of no use whatsoever to any programmer!) Wirth was vocal in his criticism and the community split for good. Algol W was a casualty of the conflict, as Wirth seems to have decided in reaction to the enormity of Algol 68 that simplicity and small size were the cardinal virtues of a language design, leading to Pascal, and then to its modular successors Modula and Oberon.

Continuing with my own perspective, I admired these designs, but when I saw Simula 67 and object-oriented programming I felt that I had come across a whole new level of expressive power, with the notion of class unifying types and modules, and stopped caring much for purely modular languages, including Ada as it was then. A particularly ill-considered feature of all these languages always irked me: the requirement that every module should be declared in two parts, interface and implementation. An example, in my view, of a good intention poorly realized and leading to nasty consequences. One of these consequences is that the information in the interface part inevitably gets repeated in the implementation part. Repetition, as David Parnas has taught us, is (particularly in the form of copy-paste) the programmer’s scary enemy. Any change needs to be checked and repeated in both the original and the duplicate. Any bug needs to be fixed in both. The better solution, instead of the interface-implementation separation, is to write everything in one place (the class of object-oriented programming) and then rely on tools to extract, from the text, the interface view but also many other interesting views abstracted from the text.

In addition, modular languages offer one implementation for each interface. How limiting! With object-oriented programming, you use inheritance to provide a general version of an abstraction and then as many variants as you like, adding them as you see fit (Open-Closed Principle) and not repeating the common information. These ideas took me towards a direction of language design completely different from Wirth’s.

One of his principles in language design was that it should be easy to write a compiler — an approach that paid off magnificently for Pascal. I mentioned above the beauty of recursive-descent parsing (an approach which means roughly that you parse a text by seeing how it starts, deducing the structure that you expect to follow, then applying the same technique recursively to the successive components of the expected structure). Recursive descent will only work well if the language is LL (1) or very close to it. (LL (1) means, again roughly, that the first element of a textual component unambiguously determines the syntactic type of that component. For example the instruction part of a language is LL (1) if an instruction is a conditional whenever it starts with the keyword if, a loop whenever it starts with the keyword while, and an assignment variable := expression whenever it starts with a variable name. Only with a near-LL (1) structure is recursive descent recursive-decent.) Pascal was designed that way.

A less felicitous application of this principle was Wirth’s insistence on one-pass compilation, which resulted in Pascal requiring any use of indirect recursion to include an early announcement of the element — procedure or data type — being used recursively. That is the kind of thing I disliked in Pascal: transferring (in my opinion) some of the responsibilities of the compiler designer onto the programmer. Some of those constraints remained long after advances in hardware and software made the insistence on one-pass compilation seem obsolete.

What most characterized Wirth’s approach to design — of languages, of machines, of software, of articles, of books, of curricula — was his love of simplicity and dislike of gratuitous featurism. He most famously expressed this view in his Plea for Lean Software article. Even if hardware progress drives software progress, he could not accept what he viewed as the lazy approach of using hardware power as an excuse for sloppy design. I suspect that was the reasoning behind the one-compilation-pass stance: sure, our computers now enable us to use several passes, but if we can do the compilation in one pass we should since it is simpler and leaner.
As in the case of Pascal, this relentless focus could be limiting at times; it also led him to distrust artificial intelligence, partly because of the grandiose promises its proponents were making at the time. For many years indeed, AI never made it into ETH computer science. I am talking here of the classical, logic-based form of AI; I had not yet had the opportunity to ask Niklaus what he thought of the modern, statistics-based form. Perhaps the engineer in him would have mollified his attitude, attracted by the practicality and well-defined scope of today’s AI methods. I will never know.

As to languages, I was looking forward to more discussions; while I wholeheartedly support his quest for simplicity, size to me is less important than simplicity of the structure and reliance on a small number of fundamental concepts (such as data abstraction for object-oriented programming), taken to their full power, permeating every facet of the language, and bringing consistency to a powerful construction.

Disagreements on specifics of language design are normal. Design — of anything — is largely characterized by decisions of where to be dogmatic and where to be permissive. You cannot be dogmatic all over, or will end with a stranglehold. You cannot be permissive all around, or will end with a mess. I am not dogmatic about things like the number of compiler passes: why care about having one, two, five or ten passes if they are fast anyway? I care about other things, such as the small number of basic concepts. There should be, for example, only one conceptual kind of loop, accommodating variants. I also don’t mind adding various forms of syntax for the same thing (such as, in object-oriented programming, x.a := v as an abbreviation for the conceptually sound x.set_a (v)). Wirth probably would have balked at such diversity.

In the end Pascal largely lost to its design opposite, C, the epitome of permissiveness, where you can (for example) add anything to almost anything. Recent languages went even further, discarding notions such as static types as dispensable and obsolete burdens. (In truth C is more a competitor to P-Code, since provides a good target for compilers: its abstraction level is close to that of the computer and operating system, humans can still with some effort decipher C code, and a C implementation is available by default on most platforms. A kind of universal assembly language. Somehow, somewhere, the strange idea creeped into people’s minds that it could also be used as a notation for human programmers.)

In any case I do not think Niklaus followed closely the evolution of the programming language field in recent years, away from principles of simplicity and consistency; sometimes, it seems, away from any principles at all. The game today is mostly “see this cute little feature in my language, I bet you cannot do as well in yours!” “Oh yes I can, see how cool my next construct is!“, with little attention being paid to the programming language as a coherent engineering construction, and even less to its ability to produce correct, robust, reusable and extendible software.

I know Wirth was horrified by the repulsive syntax choices of today’s dominant languages; he could never accept that a = b should mean something different from b = a, or that a = a + 1 should even be considered meaningful. The folly of straying away from conventions of mathematics carefully refined over several centuries (for example by distorting “=” to mean assignment and resorting to a special symbol for equality, rather than the obviously better reverse) depressed him. I remain convinced that the community will eventually come back to its senses and start treating language design seriously again.

One of the interesting features of meeting Niklaus Wirth the man, after decades of studying from the works of Professor Wirth the scientist, was to discover an unexpected personality. Niklaus was an affable and friendly companion, and most strikingly an extremely down-to-earth person. On the occasion of the 2014 symposium we were privileged to meet some of his children, all successful in various walks of life: well-known musician in the Zurich scene, specialty shop owner… I do not quite know how to characterize in words his way of speaking (excellent) English, but it is definitely impossible to forget its special character, with its slight but unmistakable Swiss-German accent (also perceptible in German). To get an idea, just watch one of the many lecture videos available on the Web. See for example the videos from the 2014 symposium mentioned above, or this full-length interview recorded in 2018 as part of an ACM series on Turing Award winners.

On the “down-to-earth” part: computer scientists, especially of the first few generations, tend to split into the mathematician types and the engineer types. He was definitely the engineer kind, as illustrated by his hardware work. One of his maxims for a successful career was that there are a few things that you don’t want to do because they are boring or feel useless, but if you don’t take care of them right away they will come back and take even more of your time, so you should devote 10% of that time to discharge them promptly. (I wish I could limit that part to 10%.)

He had a witty, subtle — sometimes caustic — humor. Here is a Niklaus Wirth story. On the seventh day of creation God looked at the result. (Side note: Wirth was an atheist, which adds spice to the choice of setting for the story.) He (God) was pretty happy about it. He started looking at the list of professions and felt good: all — policeman, minister, nurse, street sweeper, interior designer, opera singer, personal trainer, supermarket cashier, tax collector… — had some advantages and some disadvantages. But then He got to the University Professor row. The Advantages entry was impressive: long holidays, decent salary, you basically get to do what you want, and so on; but the Disadvantages entry was empty! Such a scandalous discrepancy could not be tolerated. For a moment, a cloud obscured His face. He thought and thought and finally His smile came back. At that point, He had created colleagues.

When the computing world finally realizes that design needs simplicity, it will do well to go back to Niklaus Wirth’s articles, books and languages. I can think of only a handful of people who have shaped the global hardware and software industry in a comparable way. Niklaus Wirth is, sadly, sadly gone — and I still have trouble accepting that he will not show up for dinner, on Thursday or ever again — but his legacy is everywhere.

In August I was planning for my participation in the ICTSS conference in Bergamo, Italy, and wanted to find some accommodation within walking distance of the conference place. Bergamo has a medieval “città alta”, high city, at the top of a hill, and a “città bassa”, low city, down in the valley, where modern expansion happens. I had only passed through Bergamo once before but enough to know that it is not that easy or fast to commute between the two parts, so it is better to plan your accommodation properly.

It was not immediately clear from the online map where the conference venue belonged, so I thought that maybe this was an opportunity to find some actual use for ChatGPT. (So far I am not a great fan, see here, but one has to keep one’s mind open.) I asked my question:

and received an answer (here is the first part):

Good that I did not stop here because the answer is plain wrong; the Piazzale in question (the main site of the university, and a former convent, as I later found out) is in the high city. Even more interesting was the second part of the answer:

Now this is really good. With my Southern California experience I am not that easily surprised: it is a common joke in Santa Barbara (an area prone to mudslides, particularly when it rains after a fire) that you might go to bed in your house at the top of a hill and wake up the next morning in the same house but with a whole new set of neighbors at the bottom of a valley. The other way around, though, is quite new for me.

AI-induced levitation! Of an entire city area! Since September 2021, the Piazzale San Agostino and its historic university buildings might have moved up 250 meters from low to high city. Artificial Intelligence is so amazing.

As a codicil to this little report: at that point I had decided to drop this absurd tool and look for a reliable source, but noticed that I had made a mistake in the Italian phrase: the name of high city is “città alta”, whereas I had put the words in the reverse order (as shown above). Since I like to do things right I asked the question again with the proper order, not changing anything else, not questioning the previous results, just repeating the question with a correct phrasing:

and got this:

The amazement continues. I had not complained, not questioned the answer, not emitted any doubt or criticism, and here is this tool apologizing again. And leaving me with two exactly contradictory answers. Which one am I supposed to believe? If I ask again, am I going to get a new set of excuses and a reversal to the original answer? (I did not try.)

I will continue my quest to find out whatever this thing might be good for.

Maria Naumcheva, Sophie Ebersold, Alexandr Naumchev, Jean-Michel Bruel, Florian Galinier and Bertrand Meyer: Object-Oriented Requirements: a Unified Framework for Specifications, Scenarios and Tests, in JOT (Journal of Object Technology), vol. 22, no. 1, pages 1:1-19, 2023. Available here with link to PDF  (the journal is open-access).

From the abstract:

A paradox of requirements specifications as dominantly practiced in the industry is that they often claim to be object-oriented (OO) but largely rely on procedural (non-OO) techniques. Use cases and user stories describe functional flows, not object types.

To gain the benefits provided by object technology (such as extendibility, reusability, and reliability), requirements should instead take advantage of the same data abstraction concepts – classes, inheritance, information hiding – as OO design and OO programs.

Many people find use cases and user stories appealing because of the simplicity and practicality of the concepts. Can we reconcile requirements with object-oriented principles and get the best of both worlds?

This article proposes a unified framework. It shows that the concept of class is general enough to describe not only “object” in a narrow sense but also scenarios such as use cases and user stories and other important artifacts such as test cases and oracles. Having a single framework opens the way to requirements that enjoy the benefits of both approaches: like use cases and user stories, they reflect the practical views of stakeholders; like object-oriented requirements, they lend themselves to evolution and reuse.

The article builds in part on material from chapter 7 of my requirements book (Handbook of Requirements and Business Analysis, Springer).

I harbor no illusion about the effectiveness of airing this particular pet peeve; complaining about it has about the same chance of success as protesting against split infinitives or music in restaurants. Still, it is worth mentioning that the widespread use of the word “statement” to denote a programming language element, such as an assignment, that directs a computer to perform some change, is misleading. “Instruction” is the better term.

A “statement” is “something stated, such as a single declaration or remark, or a report of fact or opinions” (Merriam-Webster).

Why does it matter? The use of “statement” to mean “instruction” obscures a fundamental distinction of software engineering: the duality between specification and implementation. Programming produces a solution to a problem; success requires expressing both the problem, in the form of a specification, and the devised solution, in the form of an implementation. It is important at every stage to know exactly where we stand: on the problem side (the “what”) or the solution side (the “how”). In his famous Goto Statement Considered Harmful of 1968, Dijkstra beautifully characterized this distinction as the central issue of programming:

Our intellectual powers are rather geared to master static relations and our powers to visualize processes evolving in time are relatively poorly developed. For that reason we should do (as wise programmers aware of our limitations) our utmost to shorten the conceptual gap between the static program and the dynamic process, to make the correspondence between the program (spread out in text space) and the process (spread out in time) as trivial as possible.

Software verification, whether conducted through dynamic means (testing) or static techniques (static analysis, proofs of correctness), relies on having separately expressed both a specification of the intent and a proposed implementation intended to realize that intent. They have to remain distinct; otherwise we cannot even define what it means that the program should be correct (correct with respect to what?), and even less what it means to validate the program (validate it against what?).

In many approaches to verification, the properties against which we validate programs are called assertions. An assertion expresses a property that should hold at some point of program execution. For example, after the assignment instruction a := b + 1, the assertion a ≠ b will hold. This notion of assertion is used both in testing frameworks, such as JUnit for Java or PyUnit for Python, and in program proving frameworks; see, for example, the interactive Web-based version of the AutoProof program-proving framework for Eiffel at autoproof.sit.org, and of course the entire literature on axiomatic (Floyd-Hoare-Dijkstra-style) verification.

The difference between the instruction and the assertion is critical: a := b + 1 tells the computer to do something (change the value of a), as emphasized here by the “:=” notation for assignment; a ≠ b does not direct the computer or the computation to do anything, but simply states a property that should hold at a certain stage of the computation if everything went fine so far.

In the second case, the word “states” is indeed appropriate: an assertion states a certain property. The expression of that property, a ≠ b, is a “statement” in the ordinary English sense of the term. The command to the computer, a := b + 1, is an instruction whose effect is to ensure the satisfaction of the statement a ≠ b. So if we use the word “statement” at all, we should use it to mean an assertion, not an instruction.

If we start calling instructions “statements” (a usage that Merriam-Webster grudgingly accepts in its last entry for the term, although it takes care to define it as “an instruction in a computer program,” emphasis added), we lose this key distinction.

There is no reason for this usage, however, since the word “instruction” is available, and entirely appropriate.

So, please stop saying “an assignment statement” or “a print statement“; say “an assignment instruction” and so on.

Maybe you won’t, but at least you have been warned.

This article was first published in the “Communications of the ACM” blog.

A full, free online version of Object Success
(1995)

I am continuing the process of releasing some of my earlier books. Already available: Introduction to the Theory of Programming Languages (see here) and Object-Oriented Software Construction, 2nd edition (see here). The latest addition is Object Success, a book that introduced object technology to managers and more generally emphasized the management and organizational consequences of OO ideas.

The text (3.3 MB) is available here for download.

Copyright notice: The text is not in the public domain. It is copyrighted material (© Bertrand Meyer, 1995, 2023), made available free of charge on the Web for the convenience of readers, with the permission of the original publisher (Prentice Hall, now Pearson Education, Inc.). You are not permitted to copy it or redistribute it. Please refer others to the present version at bertrandmeyer.com/success.

(Please do not bookmark or share the above download link as it may change, but use the present page: https:/bertrandmeyer.com/success.) The text is republished identically, with minor reformatting and addition of some color. (There is only one actual change, a mention of the evolution of hardware resources, on page 136, plus a reference to a later book added to a bibliography section on page 103.) This electronic version is fully hyperlinked: clicking entries in the table of contents and index, and any element in dark red such as the page number above, will take you to the corresponding place in the text.

The book is a presentation of object technology for managers and a discussion of management issues of modern projects. While it is almost three decades old and inevitably contains some observations that will sound naïve  by today’s standards, I feel  it retains some of its value. Note in particular:

• The introduction of a number of principles that went radically against conventional software engineering wisdom and were later included in agile methods. See Agile! The Good, the Hype and the Ugly, Springer, 2014, book page at agile.ethz.ch.
• As an important example, the emphasis on the primacy of code. Numerous occurrences of the argument throughout the text. (Also, warnings about over-emphasizing analysis, design and other products, although unlike “lean development” the text definitely does not consider them to be “waste”. See the “bubbles and arrows of outrageous fortune”, page 80.)
• In the same vein, the emphasis on incremental development.
• Yet another agile-before-agile principle: Less-Is-More principle (in “CRISIS REMEDY”, page 133).
• An analysis of the role of managers (chapters 7 to 9) which remains largely applicable, and I believe more realistic than the agile literature’s reductionist view of managers.
• A systematic analysis of what “prototyping” means for software (chapter 4), distinguishing between desirable and less good forms.
• Advice on how to salvage projects undergoing difficulties or crises (chapters 7 and 9).
• A concise exposition of OO concepts (chapter 1 and appendix).
• A systematic discussion of software lifecycle models (chapter 3), including the “cluster model”. See new developments on this topic in my recent “Handbook of Requirements and Business Analysis”, Springer, 2022, book page at bertrandmeyer.com/requirements.
• More generally, important principles from which managers (and developers) can benefit today just as much as at the time of publication.

The download link again (3.3 MB): here it is.

August of last year brought the sad news of Barry Boehm’s passing away on August 20. If software engineering deserves at all to be called engineering today, it is in no small part thanks to him.

“Engineer” is what Boehm was, even though his doctorate and other degrees were all in mathematics. He looked the part (you might almost expect him to carry a slide rule in his shirt pocket, until you realized that as a software engineer he did not need one) and more importantly he exuded the seriousness, dedication, precision, respect for numbers, no-nonsense attitude and practical mindset of outstanding engineers. He was employed as an engineer or engineering manager in the first part of his career, most notably at TRW, a large aerospace company (later purchased by Northrop Grumman), turning to academia (USC) afterwards, but even as a professor he retained that fundamental engineering ethos.

LASER Summer School, Elba Island (Italy), September 2010
From left: Walter Tichy, Barry Boehm, Vic Basili (photograph by Bertrand Meyer)

Boehm’s passion was to turn the study of software away from intuition and over to empirical enquiry, rooted in systematic objective studies of actual projects. He was not the only one advocating empirical methods (others from the late seventies on included Basili, Zelkowitz, Tichy, Gilb, Rombach, McConnell…) but he had an enormous asset: access to mines of significant data—not student experiments, as most researchers were using!—from numerous projects at TRW. (Basili and Zelkowitz had similar sources at NASA.) He patiently collected huge amounts of project information, analyzed them systematically, and started publishing paper after paper about what works for software development; not what we wish would work, but what actually does on the basis of project results.

Then in 1981 came his magnum opus, Software Engineering Economics (Prentice Hall), still useful reading today (many people inquired over the years about projects for a second edition, but I guess he felt it was not warranted). Full of facts and figures, the book also popularized the Cocomo model for cost prediction, still in use nowadays in a revised version developed at USC (Cocomo II, 1995, directly usable through a simple Web interface at softwarecost.org/tools/COCOMO/

Cocomo provides a way to estimate both the cost and the duration of a project from the estimated number of lines of code (alternatively, in Cocomo II, from the estimated number of function points), and some auxiliary parameters to account for each project’s specifics. Boehm derived the formula by fitting from thousands of projects.

When people first encounter the idea of Cocomo (even in a less-rudimentary form than the simplified one I just gave), their first reaction is often negative: how can one use a single formula to derive an estimate for any project? Isn’t the very concept ludicrous anyway since by definition we do not know the number of lines of code (or even of function points) before we have developed the project? With lines of code, how do we distinguish between different languages? There are answers to all of these questions (the formula is ponderated by a whole set of criteria capturing project specifics, lines of code calibrated by programming language level do correlate better than most other measures with actual development effort, a good project manager will know in advance the order of magnitude of the code size etc.). Cocomo II is not a panacea and only gives a rough order of magnitude, but remains one of the best available estimation tools.

Software Engineering Economics and the discussion of Cocomo also introduced important laws of software engineering, not folk wisdom as was too often (and sometimes remains) prevalent, but firm results. I covered one in an article in this blog some time ago, calling it the “Shortest Possible Schedule Theorem”: if a serious estimation method, for example Cocomo, has determined an optimal cost and time for a project, you can reduce the time by devoting more resources to the project, but only down to a certain limit, which is about 75% of the original. In other words, you can throw money at a project to make things happen faster, but the highest time reduction you will ever be able to gain is by a quarter. Such a result, confirmed by many studies (by Boehm and many others after him), is typical of the kind of strong empirical work that Boehm favored.

The CMM and CMMI models  of technical management are examples of important developments that clearly reflect Boehm’s influence. I am not aware that he played any direct role (the leader was Watts Humphrey, about whom I wrote a few years ago), but the models’ constant emphasis on measurement, feedback and assessment are in line with the principles  so persuasively argued in his articles and books.

Another of his famous contributions is the Spiral model of the software lifecycle. His early work and Software Engineering Economics had made Boehm a celebrity in the field, one of its titans in fact, but also gave him the reputation, deserved or not, of representing what may be called big software engineering, typified by the TRW projects from which he drew his initial results: large projects with large budgets, armies of programmers of variable levels of competence, strong quality requirements (often because of the mission- and life-critical nature of the projects) leading to heavy quality assurance processes, active regulatory bodies, and a general waterfall-like structure (analyze, then specify, then design, then implement, then verify). Starting in the eighties other kinds of software engineering blossomed, pioneered by the personal computer revolution and Unix, and often typified by projects, large or small but with high added value, carried out iteratively by highly innovative teams and sometimes by just one brilliant programmer. The spiral model is a clear move towards flexible modes of software development. I must say I was never a great fan (for reasons not appropriate for discussion here) of taking the Spiral literally, but the model was highly influential and made Boehm a star again for a whole new generation of programmers in the nineties. It also had a major effect on agile methods, whose notion of  “sprint ” can be traced directly the spiral. It is a rare distinction to have influenced both the CMM and agile camps of software engineering with all their differences.

This effort not to remain wrongly identified with the old-style massive-project software culture, together with his natural openness to new ideas and his intellectual curiosity, led Boehm to take an early interest in agile methods; he was obviously intrigued by the iconoclasm of the first agile publications and eager to understand how they could be combined with timeless laws of software engineering. The result of this enquiry was his 2004 book (with Richard Turner) Balancing Agility and Discipline: A Guide for the Perplexed, which must have been the first non-hagiographic presentation (still measured, may be a bit too respectful out of a fear of being considered old-guard) of agile approaches.

Barry Boehm was an icon of the software engineering movement, with the unique position of having been in essence present at creation (from the predecessor conference of ICSE in 1975) and accompanying, as an active participant, the stupendous growth and change of the field over half a century.

Barry Boehm at a dinner at ICSE 2006, Shanghai (photograph by Bertrand Meyer)

I was privileged to meet Barry very early, as we were preparing a summer school in 1978 on Programming Methodology where the other star was Tony Hoare. It was not clear how the mix of such different personalities, the statistics-oriented UCLA-graduate American engineer and the logic-driven classically-trained (at Oxford) British professor would turn out.

Boehm could be impatient with cryptic academic pursuits; one exercise in Software Engineering Economics (I know only a few other cases of sarcasm finding its refuge in exercises from textbooks) presents a problem in software project management and asks for an answer in multiple-choice form. All the proposed choices are sensible management decisions, except for one which goes something like this: “Remember that Bob Floyd [Turing-Awarded pioneer of algorithms and formal verification] published in Communications of the ACM vol. X no. Y pages 658-670 that scheduling of the kind required can be performed in O (n³ log log n) instead of O (n³ log n) as previously known; take advantage of this result to spend 6 months writing an undecipherable algorithm, then discover that customers do not care a bit about the speed.” (Approximate paraphrase from memory [1].)

He could indeed be quite scathing of what he viewed as purely academic pursuits removed from the reality of practical projects. Anyone who attended ICSE 1979 a few months later in Munich will remember the clash between him and Dijkstra; the organizers had probably engineered it (if I can use that term), having assigned them the topics  “Software Engineering As It Is” and “Software Engineering as It Should Be”, but it certainly was spectacular. There had been other such displays of the divide before. Would we experience something of the kind at the summer school?

No clash happened; rather, the reverse, a meeting of minds. The two sets of lectures (such summer schools lasted three weeks at that time!) complemented each other marvelously, participants were delighted, and the two lecturers also got along very well. They were, I think, the only native English speakers in that group, they turned out to have many things in common (such as spouses who were also brilliant software engineers on their own), and I believe they remained in contact for many years. (I wish I had a photo from that school—if anyone reading this has one, please contact me!)

Barry was indeed a friendly, approachable, open person, aware of his contributions but deeply modest.

Few people leave a profound personal mark on a field. A significant part of software engineering as it is today is a direct consequence of Barry’s foresight.

Note

[1] The full text of the exercise will appear shortly as a separate article on this blog.

A version of this article appeared previously in the Communications of the ACM blog.

Often,  “we do this and then we do that” is just a lazy way of stating “to do that, we must have achieved this.” The second form is more general than the first, since there may be many things you can “do” to achieve a certain condition.

The extra generality is welcome for software requirements, which should describe essential properties without over-specifying, in particular without prescribing a specific ordering of operations  when it is only one possible sequence among several, thereby restricting the flexibility of designers and implementers.

This matter of logical versus sequential constraints is at the heart of the distinction between scenario-based techniques — use cases, user stories… — and object-oriented requirements. This article analyzes the distinction. It is largely extracted from my recent textbook, the Handbook of Requirements and Business Analysis [1], which contains a more extensive discussion.

1. Scenarios versus OO

Scenario techniques, most significantly use cases and user stories, have become dominant in requirements. They obviously fill a need and are intuitive to many people. As a general requirement technique, however, they lack abstraction. Assessed against object-oriented requirements techniques, they suffer from the same limitations as procedural (pre-OO)  techniques against their OO competitors in the area of design and programming. The same arguments that make object technology subsume non-OO approaches in those areas transpose to requirements.

Scenario techniques describe system properties in terms of a particular sequence of interactions with the system. A staple example of a use case is ordering a product through an e-commerce site, going through a number of steps. In contrast, an OO specification presents a certain number of abstractions and operations on them, chracterized by their logical properties. This description may sound vague, so we move right away to examples.

2. Oh no, not stacks again

Yes, stacks. This example is rather computer-sciency so it is not meant to convince anyone but just to explain the ideas. (An example more similar to what we deal with in the requirements of industry projects is coming next.)

A stack is a LIFO (Last-In, First-Out) structure. You insert and remove elements at the same end.

Think of a stack of plates, where you can deposit one plate at a time, at the top, and retrieve one plate at a time, also at the top. We may call the two operations put and remove. Both are commands (often known under the alternative names push and pop). We will also use an integer query count giving the number of elements.

Assume we wanted to specify the behavior of a stack through use cases. Possible use cases (all starting with an empty stack) are:

/1/

put
put ; put
put ; put ; put        — etc.: any number of successive put (our stacks are not bounded)
put ; remove
put ; put ; remove
put ; put ; remove ; remove
put ; put ; remove ; remove ; put ; remove

We should also find a way to specify that the system does not support such use cases as

/2/

remove ; put

or even just

/3/

remove

We could keep writing such use cases forever — some expressing normal sequences of operations, others describing erroneous cases — without capturing the fundamental rule that at any stage, the number of put so far has to be no less than the number of remove.

A simple way to capture this basic requirement is through logical constraints, also known as contracts, relying on assertions: preconditions which state the conditions under which an operation is permitted, and postconditions which describe properties of its outcome. In the example we can state that:

• put has no precondition, and the postcondition

          count = old count + 1

using the old notation to refer to the value of an expression before the operation (here, the postcondition states that put increases count by one).

• remove has the precondition

count > 0

and the postcondition

count = old count – 1

since it is not possible to remove an element from an empty stack. More generally the LIFO discipline implies that we cannot remove more than we have put.(Such illegal usage sequences are sometimes called “misuse cases.”)

(There are other properties, but the ones just given suffice for this discussion.)

The specification states what can be done with stacks (and what cannot) at a sufficiently high level of abstraction to capture all possible use cases. It enables us to keep track of the value of count in the successive steps of a use case; it tells us for example that all the use cases under /1/ above observe the constraints: with count starting at 0, taking into account the postconditions of put and remove, the precondition of every operation will be satisfied prior to all of its calls. For /2/ and /3/ that is not the case, so we know that these use cases are incorrect.

Although this example covers a data structure, not  requirements in the general sense, it illustrates how logical constraints are more general than scenarios:

• Use cases, user stories and other  forms of scenario only describe specific instances of behavior.
• An OO model with contracts yields a more abstract specification, to which individual scenarios can be shown to conform, or not.

3. Avoiding premature ordering decisions

As the stack example illustrates, object-oriented specifications stay away from premature time-order decisions by focusing on object types (classes) and their operations (queries and commands), without making an early commitment to the order of executing these operations.

In the book, I use in several places a use-case example from one of the best books about use cases (along with Ivar Jacobson’s original one of course): Alistair Cockburn’s Writing Effective Use Cases (Pearson Education, 2001). A simplified form of the example is:

1. A reporting party who is aware of the event registers a loss to the insurance company.

2. A clerk receives and assigns claim to a claims agent.

3. The assigned claims adjuster:

3.1 Conducts an investigation.
3.2 Evaluates damages.
3.3 Sets reserves.
3.4 Negotiates the claim.
3.5 Resolves the claim and closes it.

(A reserve in the insurance business is an amount that an insurer, when receiving a claim, sets aside as to cover the financial liability that may result from the claim.)

As a specification, this scenario is trying to express useful things; for example, you must set reserves before starting to negotiate the claim. But it expresses them in the form of a strict sequence of operations, a temporal constraint which does not cover the wide range of legitimate scenarios. As in the stack example, describing a few such scenarios is helpful as part of requirements elicitation, but to specify the resulting requirements it is more effective to state the logical constraints.

Here is a sketch (in Eiffel) of how a class INSURANCE_CLAIM could specify them in the form of contracts. Note the use of require to introduce a precondition and ensure for postconditions.

class INSURANCE_CLAIM feature

        — Boolean queries (all with default value False):
    is_investigated, is_evaluated, is_reserved,is_agreed,is_imposed, is_resolved:

BOOLEAN

    investigate
                — Conduct investigation on validity of claim. Set is_investigated.
        deferred
        ensure
            is_investigated
        end

    evaluate
                — Assess monetary amount of damages.
        require
            is_investigated
        deferred
        ensure
            is_evaluated
            — Note: is_investigated still holds (see the invariant at the end of the class text).
        end

    set_reserve
                — Assess monetary amount of damages. Set is_reserved.
        require
            is_investigated
            — Note: we do not require is_evaluated.
        deferred
        ensure
            is_reserved
        end
 

    negotiate
                — Assess monetary amount of damages. Set is_agreed only if negotiation
                — leads to an agreement with the claim originator.
        require
                   is_reserved
is_evaluated                       
        deferred
        ensure
            is_reserved
            — See the invariant for is_evaluated and is_investigated.
        end

    impose (amount: INTEGER)
                — Determine amount of claim if negotiation fails. Set is_imposed.
        require
            not is_agreed
            is_reserved
        deferred
        ensure
            is_imposed
        end

    resolve
                — Finalize handling of claim. Set is_resolved.
        require
            is_agreed or is_imposed
        deferred
        ensure
            is_resolved
        end

invariant                    — “⇒” is logical implication.

is_evaluated ⇒ is_investigated
is_reserved  ⇒ is_evaluated
is_resolved ⇒ is_agreed or is_imposed
is_agreed ⇒ is_evaluated
is_imposed ⇒ is_evaluated
is_imposed ⇒ not is_agreed
                          — Hence, by laws of logic, is_agreed ⇒ not is_imposed

end

Notice the interplay between the preconditions, postconditions and class invariant, and the various boolean-valued queries they involve (is_investigated, is_evaluated, is_reserved…). You can specify a strict order of operations o₁, o₂ …, as in a use case, by having a sequence of assertions p_i such that operation o_i has the contract clauses require p_i and ensure p_i+1; but assertions also enable you to specify a much broader range of allowable orderings as all acceptable.
The class specification as given is only a first cut and leaves many aspects untouched. It will be important in practice, for example, to include a query payment describing the amount to be paid for the claim; then impose has the postcondition payment = amount, and negotiate sets a certain amount for payment.
Even in this simplified form, the specification includes a few concepts that the original use case left unspecified, in particular the notion of imposing a payment (through the command impose) if negotiation fails. Using a logical style typically uncovers such important questions and provides a framework for answering them, helping to achieve one of the principal goals of requirements engineering.

4. Logical constraints are more general than sequential orderings

The specific sequence of actions described in the original use case (“main success scenario”) is compatible with the logical constraints: you can check that in the sequence

investigate
evaluate
set_reserve
negotiate
resolve

the postcondition of each step implies the precondition of the next one (the first has no precondition). In other words, the temporal specification satisfies the logical one. But you can also see that prescribing this order is a case of overspecification: other orderings also satisfy the logical specification. It may be possible for example — subject to confirmation by Subject-Matter Experts — to change the order of evaluate and set_reserve, or to perform these two operations in parallel.

The specification does cover the fundamental sequencing constraints; for example, the pre- and postcondition combinations imply that investigation must come before evaluation and resolution must be preceded by either negotiation or imposition. But they avoid the non-essential constraints which, in the use case, were only an artifact of the sequential style of specification, not a true feature of the problem.

The logical style is also more conducive to conducting a fruitful dialogue with domain experts and stakeholders:

• With a focus on use cases, the typical question from a requirements engineer (business analyst) is “do you do A before doing B?” Often the answer will be contorted, as in “usually yes, but only if C, oh and sometimes we might start with B if D holds, or we might work on A and B in parallel…“, leading to vagueness and to more complicated requirements specifications.
• With logic-based specifications, the two fundamental question types are: “what conditions do you need before doing B?” and “does doing A ensure condition C?”. They force stakeholders to assess their own practices and specify precisely the relations between operations of interest.

5. What use for scenarios?

Use-cases and more generally scenarios, while more restrictive than logical specifications, remain important as complements to specifications. They serve as both input and output to more abstract requirements specifications (such as OO specifications with contracts):

• As input to requirements: initially at least, stakeholders and Subject-Matter Experts often find it intuitive to describe typical system interactions, and their own activities, in the form of scenarios. Collecting such scenarios is an invaluable requirements elicitation technique. The requirements engineer must remember that any such scenario is just one example walk through the system, and must abstract from these examples to derive general logical rules.
• As output from requirements: from an OO specification with its contracts, the requirements engineers can produce valid use cases. “Valid” means that the operation at every step satisfies the applicable precondition, as a consequence of the previous steps’ postconditions and of the class invariant. The requirements engineers can then submit these use cases to the SMEs and through them to stakeholders to confirm that they make sense, update the logical conditions if they do not (to rule out bad use cases), and check the results they are expected to produce.

6. Where do scenarios fit?

While many teams will prefer to write scenarios (for the purposes just described) in natural language, it is possible to go one step further and, in an object-oriented approach to requirements, gather scenarios in classes. But that point exceeds the scope of the present sketch. We will limit ourselves here to the core observation: logical constraints subsume sequential specifications; you can deduce the ltter from the former, but not the other way around; and focusing on abstract logical specifications leads to a better understanding of the requirements.

Reference

Bertrand Meyer: Handbook of Requirements and Business Analysis, Springer, 2022. See the book page with sample chapters and further material here.

(This article was first published on the Communications of the ACM blog.)

Li Huang (PhD student at SIT) will be presenting at an ISSRE workshop the paper Improving Counterexample Quality from Failed Program Verification, written with Manuel Oriol and me. One can find the text on arXiv here. (I will update this reference with the official publication link when I have it.)

The result being presented is part of a more general effort at combining proofs and tests (with other papers in the pipeline). The idea of treating proofs and tests as complementary rather than competing methods of software verification is an old pursuit of mine (which among other consequences resulted in the creation with Yuri Gurevich of the Tests and Proofs conference, which I see is continuing to run). A particular observation is that failure means a different thing for proofs and tests.

A failed test provides interesting information (in fact it is a successful proof — of incorrectness). A successful proof is, of course, also interesting (in principle it should be end of the story), whereas a successful test tells us very little. But in the practice of program proving the common occurrence is failure to prove a program element correct. You are typically left with no clue as to the source of the failure. In the AutoProof verification system for Eiffel, we are able to rely on the underlying technology (Boogie and Z3) to extract a counterexample which gives concrete evidence: as with a failed test, a programmer can in general quickly understand what is wrong.

In other words, the useless negative result of the bottom-left entry of the above picture can produce a useful result:

The general approach is the subject of another article but this one focuses on producing tests that are actually significant for the programmer. If you get very large values, you will not immediately be able to relate to them. Hence the need for a process of minimization, described in the article. The results on our examples are encouraging, making it possible to evidence the bug on very small integer values.

Reference

Li Huang, Bertrand Meyer and Manuel Oriol: Improving Counterexample Quality from Failed Program Verification, 6th International Workshop on Software Faults, October 2022. Preprint available on arXiv here. The program workshop is available here; the presentation is on Monday, 31 October, 15:55 CET (7:55 AM Los Angeles, 10:55 New York).

I am happy to announce the publication of the Handbook of Requirements and Business Analysis (Springer, 2022).

It is the result of many years of thinking about requirements and how to do them right, taking advantage of modern principles of software engineering. While programming, languages, design techniques, process models and other software engineering disciplines have progressed considerably, requirements engineering remains the sick cousin. With this book I am trying to help close the gap.

The Handbook introduces a comprehensive view of requirements including four elements or PEGS: Project, Environment, Goals and System. One of its principal contributions is the definition of a standard plan for requirements documents, consisting of the four corresponding books and replacing the obsolete IEEE 1998 structure.

The text covers both classical requirements techniques and novel topics such as object-oriented requirements and the use of formal methods.

The successive chapters address: fundamental concepts and definitions; requirements principles; the Standard Plan for requirements; how to write good requirements; how to gather requirements; scenario techniques (use cases, user stories); object-oriented requirements; how to take advantage of formal methods; abstract data types; and the place of requirements in the software lifecycle.

The Handbook is suitable both as a practical guide for industry and as a textbook, with over 50 exercises and supplementary material available from the book’s site.

You can find here a book page with the preface and sample chapters.

To purchase the book, see the book page at Springer and the book page at Amazon US.

Short version: the full text of my Introduction to the Theory of Programming Languages book (second printing, 1991) is now available. This page has more details including the table of chapters, and a link to the PDF (3.3MB, 448 + xvi pages).

The book is a survey of methods for language description, particularly semantics (operational, translational, denotational, axiomatic, complementary) and also serves as an introduction to formal methods. Obviously it would be written differently today but it may still have its use.

A few days ago I released the Axiomatic Semantics chapter of the book, and the chapter introducing mathematical notations. It looked at the time that I could not easily  release the rest in a clean form, because it is impossible or very hard to use the original text-processing tools (troff and such). I could do it for these two chapters because I had converted them years ago for my software verification classes at ETH.

By perusing old files, however,  I realized that around the same time (early 2000s) I actually been able to produce PDF versions of the other chapters as well, even integrating corrections to errata  reported after publication. (How I managed to do it then I have no idea, but the result looks identical, save the corrections, to the printed version.)

The figures were missing from that reconstructed version (I think they had been produced with Brian Kernighan’s PIC graphical description language , which is even more forgotten today than troff), but I scanned them from a printed copy and reinserted them into the PDFs.

Some elements were missing from my earlier resurrection: front matter, preface, bibliography, index. I was able to reconstruct them from the original troff source using plain MS Word. The downside is that they are not hyperlinked; the index has the page numbers (which may be off by 1 or 2 in some cases because of reformatting) but not hyperlinks to the corresponding occurrences as we would expect for a new book. Also, I was not able to reconstruct the table of contents; there is only a chapter-level table of contents which, however, is hyperlinked (in other words, chapter titles link to the actual chapters). In the meantime I obtained the permission of the original publisher (Prentice Hall, now Pearson Education Inc.).

Here again is the page with the book’s description and the link to the PDF:

bertrandmeyer.com/ITPL

I have released for general usage the chapter on axiomatic semantics of my book Introduction to the Theory of Programming Languages. It’s old but I think it is still a good introduction to the topic. It explains:

• The notion of theory (with a nice — I think — example borrowed from an article by Luca Cardelli: axiomatizing types in lambda calculus).
• How to axiomatize a programming language.
• The notion of assertion.
• Hoare-style pre-post semantics, dealing with arrays, loop invariants etc.
• Dijkstra’s calculus of weakest preconditions.
• Non-determinism.
• Dealing with routines and recursion.
• Assertion-guided program construction (in other words, correctness by construction), design heuristics (from material in an early paper at IFIP).
• 26 exercises.

The text can be found at

https://se.inf.ethz.ch/~meyer/publications/theory/09-axiom.pdf

It remains copyrighted but can be used freely. It was available before since I used it for courses on software verification but the link from my publication page was broken. Also, the figures were missing; I added them back.

I thought I only had the original (troff) files, which I have no easy way to process today, but just found PDFs for all the chapters, likely produced a few years ago when I was still able to put together a working troff setup. They are missing the figures, which I have to scan from a printed copy and reinsert. I just did it for the chapter on mathematical notations, chapter 2, which you can find at https://se.inf.ethz.ch/~meyer/publications/theory/02-math.pdf. If there is interest I will release all chapters (with corrections of errata reported by various readers over the years).

The chapters of the book are:

• (Preface)

1. Basic concepts
2. Mathematical background (available through the link above).
3. Syntax (introduces formal techniques for describing syntax, included a simplified BNF).
4. Semantics: the main approaches (overview of the techniques described in detail in the following chapters).
5. Lambda calculus.
6. Denotational semantics: fundamentals.
7. Denotational semantics: language features (covers denotational-style specifications of records, arrays, input/output etc.).
8. The mathematics of recursion (talks in particular about iterative methods and fixpoints, and the bottom-up interpretation of recursion, based on work by Gérard Berry).
9. Axiomatic semantics (available through the link above).
10. Complementary semantic definitions (establishing a clear relationship between different specifications, particular axiomatic and denotational).

• Bibliography

Numerous exercises are included. The formal models use throughout a small example language called Graal (for “Great Relief After Ada Lessons”).  The emphasis is on understanding programming and programming languages through simple mathematical models.

My book Object-Oriented Software Construction, 2nd edition (see the Wikipedia page) has become hard to get. There are various copies floating around the Web but they often use bad typography (wrong colors) and are unauthorized.

In response to numerous requests and in anticipation of the third edition I have been able to make it available electronically (with the explicit permission of the original publisher).

You can find the link on another page on this site. (In sharing or linking please use that page, not the URL of the actual PDF which might change.)

I hope having the text freely available proves useful.

The Chair of Software Engineering, my group at the Schaffhausen Institute of Technology in Switzerland (SIT), has open positions for both PhD students and postdocs. We are looking for candidates with a passion for reliable software and a mix of theoretical knowledge and practical experience in software engineering. Candidates should have degrees in computer science or related fields: a doctorate for postdoc positions, a master’s degree for PhD positions. Postdoc candidates should have a substantial publication record. Experience is expected in one or more of the following fields:

• Software verification (axiomatic, model-checking, abstract interpretation etc.).
• Advanced techniques of software testing.
• Formal methods, semantics of programming languages.
• Concurrent programming.
• Design by Contract, Eiffel, techniques of correctness-by-construction.

Some of the work involves the AutoProof framework, under development at SIT (earlier at ETH), although other topics are also available, particularly in static analysis.

Compensation is attractive. Candidates must have the credentials to work in Switzerland (typically, citizenship or residence in Switzerland or the EU). Although we work in part remotely like everyone else these days, the positions are residential.

Interested candidates should send a CV and relevant documents or links (and any questions) to bm@sit.org.

Today (well, tomorrow as of writing, but when you see this it will probably be today for you) I am participating in a panel discussion with Ivar Jacobson, Robert Martin and Carlos Zapata on “The Future of Methods”, hosted by the SEMAT/Essence movement. It takes place at 18:30 CET (i.e. Paris/Zurich etc.), 12:30 EDT, 9:30 in California. It’s free, but requires registration at https://www.meetup.com/essence-for-agility/events/280316615/.

Should be a good discussion!

Requirements documents for software projects in industry, agile or not, typically follow a plan defined in a 1998 IEEE standard (IEEE 830-1998 [1]),  “reaffirmed” in 2009. IEEE 830 has the merit of simplicity, as it fits in 37 pages of which just a few (competently) describe basic requirements concepts and less than 10 are devoted to explaining the standard recommended plan, which itself consists of 3 sections with subsections. Simplicity is good but the elementary nature of the IEEE-830 plan is just not up to the challenges of modern information technology. It is time to retire this venerable precursor and move to a structure that works for the kind of ambitious, multi-faceted IT systems we build today.

For the past few years I have worked on defining a systematic approach to requirements, culminating in a book to be published in the Fall, Handbook of Requirements and Business Analysis. One of the results of this effort is a standard plan, based on the “PEGS” view of requirements where the four parts cover Project, Environment, Goals and System. The details are in the book (for some of the basic concepts see a paper at TOOLS 2019, [2]). Here I will introduce some of the key principles, since they are already  be used — as various people have done since I first started presenting the ideas in courses and seminars (particularly an ACM Webinar, organized by Will Tracz last March, whose recording is available on YouTube, and another hosted by Grady Booch for IBM).

The starting point, which gives its name to the approach, is that requirements should cover the four aspects mentioned, the four “PEGS”, defined as follows:

• A Goal is a result desired by an organization.
• A System is a set of related artifacts, devised to help meet certain goals.
• A Project is the set of human processes involved in the planning, construction, revision and  operation of a system.
• An Environment is the set of entities (such as people, organizations, devices and other material objects, regulations and other systems) external to the project and system but with the potential to affect the goals, project or system or to be affected by them.

The recommended standard plan consequently consists of four parts or books.

This proposed standard does not prescribe any particular approach to project management, software development, project lifecycle or requirements expression, and is applicable in particular to both traditional (“waterfall”) and agile projects. It treats requirements as a project activity, not necessarily a lifecycle step. One of the principles developed in the book is that requirements should be treated as a dynamic asset of the project, written in a provisional form (more or less detailed depending on the project methodology) at the beginning of the project, and then regularly extended and updated.

Similarly, the requirements can be written using any appropriate notation and method, from the most informal to the most mathematical.  In a recently published ACM Computing Surveys paper [3], my colleagues and I reviewed the various levels of formalism available  in today’s requirements approaches. The standard plan is agnostic with respect to this matter.

The books may reference each other but not arbitrarily. The permitted relations are as follows:

Note in particular that the description of the Goals should leave out technical details and hence may not refer to Project and System elements, although it may need to explain the properties of the Environment that influence or constrain the business goals. The Environment exists independently of the IT effort, and hence the Environment book should not reference any of the others, with the possible exception (dotted arrow in the figure) of effects of the System if it is to change the environment. (For example, a payroll IT system may affect the payroll process; a heating system may affect the ambient temperature.)

The multi-book structure of the recommended PEGS standard plan already goes beyond the traditional view of a single, linear “requirements document”. The books themselves are not necessarily written as linear texts; with today’s technology, requirements parts can and generally should be stored in a requirements repository which includes all requirements-relevant elements.  A linear form remains necessary; it can be either written as such or produced by tools from elements in the repository.

The standard plan defines the structure of the four PEGS books down to one more level, chapters. For any further levels (sections), each organization can define its own rules. Books can also include front and back matter, including for example  tables of contents, legal disclaimers, revision history etc., not covered by the standard structure. Here is that structure:

It is meant to be self-explanatory, but here are a few comments on each of the books:

• One of the products of the requirements effort should be to help plan and manage  the rest of the Project. This is the goal of the Project book; note in particular P.4 and P.5 covering tasks and deadlines. P.7 starts out at the beginning of the project as a blueprint for the requirements effort, and as this effort proceeds (stakeholder interviews, stakeholder workshops, competitive analysis, requirements writing …) can be regularly updated to report on how it went. (This feature is an example of treating the requirements repository and documents as a living, dynamic asset, as noted above.)
• In the Environment book, constraints (E.3) are properties of the environment (the problem domain) imposed on the project and system. Effects (E.5) go the other way around, describing how the system may affect the environment. Invariants (E.6) do both. Assumptions (E.4) are properties that are taken for granted to simplify the construction of the system (for example, a maximum number of simultaneous users), as distinct from actual constraints.
• The Goals book is intended for a less technical audience than the other books: it must be understandable to decision makers and non-IT-savvy stakeholders. It includes a short summary (G.4) of functionality, a kind of capsule version of the System book trimmed down to the essentials. Note the importance of specifying (in G.6) what aspects the system is not intended to address. The Goals book can include some (G.5) usage scenarios expressed in terms meaningful to the book’s constituencies and hence remaining at a high level of generality.
• Detailed usage scenarios will appear in the System book (S.4).  It is important to prioritize the functions (S.5), allowing a reasoned approach (rather than decisions made in a panic) if the project hits roadblocks and must sacrifice some of the functionality.

A naïve but still widely encountered view of requirements is that they serve to  “describe what the system will do” (independently of how it will do it). In the structure above, it corresponds to just one-fourth of the requirements effort, the System part. Work on requirements engineering in the past few decades has emphasized, among other concepts, the need to separate system and environment properties (Michael Jackson, Pamela Zave) and the importance of goals (Axel van Lamsweerde).

The plan reflects this richness of the requirements concept and I hope it can help many projects produce better requirements for better software.

References

[1] IEEE 830-1998, available here.

[2] Bertrand Meyer, Jean-Michel Bruel, Sophie Ebersold, Florian Galinier and Alexandr Naumchev: The Anatomy of Software Requirements, in TOOLS 2019, Springer Lecture Notes in Computer Science 11771, 2019, pages 10-40.

[3] Jean-Michel Bruel, Sophie Ebersold, Florian Galinier, Manuel Mazzara, Alexander Naumchev and Bertrand Meyer:  The Role of Formalism in System Requirements, in  Computing Surveys (ACM), vol. 54, no. 5, June 2021, pages 1-36, DOI: https://doi.org/10.1145/3448975, preprint available here.

A version of this article appeared earlier in the Communications of the ACM blog.

There is a new paper out, several years in the making:

The Role of Formalism in System Requirements
Jean-Michel Bruel, Sophie Ebersold, Florian Galinier, Manuel Mazzara, Alexander Naumchev, Bertrand Meyer
Computing Surveys (ACM), vol. 54, no. 5, June 2021, pages 1-36
DOI: https://doi.org/10.1145/3448975
Preprint available here.

The authors are from the Schaffhausen Institute of Technology in Switzerland, the University of Toulouse in France and Innopolis University in Russia. We make up a cross-institutional (and unofficial) research group which has for several years now been working on improving the state of software requirements, with both an engineering perspective and an interest in taking advantage of formal methods.

The article follows this combined formal-informal approach by reviewing the principal formal methods in requirements but also taking into consideration non-formal ones — including techniques widely used in industry, such as DOORS — and studying how they can be used in a more systematic way. It uses a significant example (a “Landing Gear System” or LGS for aircraft) to compare them and includes extensive tables comparing the approaches along a number of systematic criteria.

Here is the abstract:

A major determinant of the quality of software systems is the quality of their requirements, which should be both understandable and precise. Most requirements are written in natural language, which is good for understandability but lacks precision.

To make requirements precise, researchers have for years advocated the use of mathematics-based notations and methods, known as “formal.” Many exist, differing in their style, scope, and applicability.

The present survey discusses some of the main formal approaches and compares them to informal methods.The analysis uses a set of nine complementary criteria, such as level of abstraction, tool availability, and traceability support. It classifies the approaches into five categories based on their principal style for specifying requirements: natural-language, semi-formal, automata/graphs, mathematical, and seamless (programming-language-based). It includes examples from all of these categories, altogether 21 different approaches, including for example SysML, Relax, Eiffel, Event-B, and Alloy.

The review discusses a number of open questions, including seamlessness, the role of tools and education, and how to make industrial applications benefit more from the contributions of formal approaches.

For me, of course, this work is the continuation of a long-running interest in requirements and specifications and how to express them using the tools of mathematics, starting with a 1985 paper, still being cited today, with a strikingly similar title: On Formalism in Specifications.

Trivia: the “response to referees” (there were no fewer than eight of them!) after the first review took up 85 pages. Maybe not for the Guinness Book, but definitely a personal record. (And an opportunity to thank the referees for detailed comments that considerably helped shape the final form of the paper.)

Correction (20 July 2021): I just noted that I had forgotten to list myself among the authors! Not a sign of modesty (I don’t have any), more of absent-mindedness. Now corrected.

This Wednesday (still “tomorrow” as I am writing this), 10 March 2021, I am giving a talk on “The Beauty of Software” on the occasion of the graduation ceremony of the first students of the Schaffhausen Institute of Technology. The event starts at 17 Schaffhausen/Zurich/Paris etc. time (11 AM New York, 8 AM San Francisco) and my own talk, starting half an hour later, will take about one hour.

The talk is (surprise!) given online. Registration is free but required: you can find the registration form on the announcement page here.

The abstract appears below. It is rather ambitious-sounding and I cannot promise the talk will live up to the promise, but I feel it necessary at least to attempt some initial steps towards a better understanding of beauty in software, which might help understand beauty in general.

The Beauty of Software

Software runs the world and delivers riches. Every passionate software engineer or computer scientist is also attuned to another of its features: the study and practice of software construction reveal gems of utter beauty.

While the concept of beauty is most naturally associated with art, scientists and engineers of all fields often invoke it. Beauty is a strong guiding principle in searching for solutions to scientific and technical problems, and arbitrating between rival candidate solutions. The reaction is often instinctive: “What an elegant theory!” “This technique is too ugly to be a viable approach”.

What do such appeals to beauty really mean? Do they pertain to the same concept of beauty as found in nature and art? Is beauty only “in the eye of the beholder”, is it conditioned by cultural prejudices, or does it submit to an objective definition?

In this talk, an initial step towards a more extensive study of what beauty means for software, I will present a few artifacts from software engineering and computer science which I find strikingly beautiful and – at the risk of breaking the charm – analyze what might make them so. This analysis will lead to a tentative definition of a notion both alluring and elusive: beauty.

In the software engineering family requirements engineering is in my experience the poor cousin, lagging behind the progress of other parts (such as design). I have been devoting attention to the topic in recent months and am completing a book on the topic.

Tomorrow (Thursday), I will be covering some of the material in a one-hour Tech Talk for ACM, with the title

The Four PEGS of Requirements Engineering

The time is Thursday, 4 March 2021, at noon EDT (New York) and 18 CET (Paris, Zurich etc.). Attendance is free but requires registration, on the event page  here.

Abstract:

Bad software requirements can jeopardize projects. There is a considerable literature on requirements, but practice is far behind: what passes for requirements in industry usually consists of a few use cases or user stories, which are useful but not sufficient as a solution. Can we fix requirements engineering (known in other circles as business analysis) so that it is no longer the weak link in software engineering?

I will present ongoing work intended to help industry produce more useful requirements. It includes precise definitions of requirements concepts and a standard plan for requirements specifications, intended to replace the venerable but woefully obsolete IEEE standard from 1998. The plan contains four books covering the four “PEGS” of requirements engineering (which I will explain). The approach builds on existing knowledge to define a practical basis for requirements engineering and provide projects with precise and helpful guidelines.

This is I think the fourth time I am giving talks in this venue (previous talks were about Design by Contract, Agile Methods and Concurrency).

Science progresses through people taking advantage of others’ insights and inventions. One of the conditions that makes the game possible is that you acknowledge what you take. For the originator, it is rewarding to see one’s ideas reused, but frustrating when that happens without acknowledgment, especially when you are yourself punctilious about citing your own sources of inspiration.

I have started to record some concepts that are widely known and applied today and which I believe I originated in whole or in part, whether or not their origin is cited by those who took them. The list below is not complete and I may update it in the future. It is not a list of ideas I contributed, only of those fulfilling two criteria:

• Others have built upon them.  (If there is an idea that I think is great but no one paid attention to it, the list does not include it.)
• They have gained wide visibility.

There is a narcissistic aspect to this exercise and if people want to dismiss it as just showing I am full of myself so be it. I am just a little tired of being given papers to referee that state that genericity was invented by Java, that no one ever thought of refactoring before agile methods, and so on. It is finally time to state some facts.

Facts indeed: I back every assertion by precise references. So if I am wrong — i.e. someone preceded me — the claims of precedence can be refuted; if so I will update or remove them. All articles by me cited in this note are available (as downloadable PDFs) on my publication page. (The page is up to date until 2018; I am in the process of adding newer publications.)

Post-publication note: I have started to receive some comments and added them in a Notes section at the end; references to those notes are in the format [A].

Final disclaimer (about the narcissistic aspect): the exercise of collecting such of that information was new for me, as I do not usually spend time reflecting on the past. I am much more interested in the future and definitely hope that my next contributions will eclipse any of the ones listed below.

Programming concepts: substitution principle

Far from me any wish to under-represent the seminal contributions of Barbara Liskov, particularly her invention of the concept of abstract data type on which so much relies. As far as I can tell, however, what has come to be known as the “Liskov Substitution Principle” is essentially contained in the discussion of polymorphism in section 10.1 of in the first edition (Prentice Hall, 1988) of my book Object-Oriented Software Construction (hereafter OOSC1); for example, “the type compatibility rule implies that the dynamic type is always a descendant of the static type” (10.1.7) and “if B inherits from A, the set of objects that can be associated at run time with an entity [generalization of variable] includes instances of B and its descendants”.

Perhaps most tellingly, a key aspect of the substitution principle, as listed for example in the Wikipedia entry, is the rule on assertions: in a proper descendant, keep the invariant, keep or weaken the precondition, keep or strengthen the postcondition. This rule was introduced in OOSC1, over several pages in section 11.1. There is also an extensive discussion in the article Eiffel: Applying the Principles of Object-Oriented Design published in the Journal of Systems and Software, May 1986.

The original 1988 Liskov article cited (for example) in the Wikipedia entry on the substitution principle says nothing about this and does not in fact include any of the terms “assertion”, “precondition”, “postcondition” or “invariant”. To me this absence means that the article misses a key property of substitution: that the abstract semantics remain the same. (Also cited is a 1994 Liskov article in TOPLAS, but that was many years after OOSC1 and other articles explaining substitution and the assertion rules.)

Liskov’s original paper states that “if for each object o1 of type S there is an object o2 of type T such that for all programs P defined in terms of T, the behavior of P is unchanged when o1 is substituted for oz, then S is a subtype of T.” As stated, this property is impossible to satisfy: if the behavior is identical, then the implementations are the same, and the two types are identical (or differ only by name). Of course the concrete behaviors are different: applying the operation rotate to two different figures o1 and o2, whose types are subtypes of FIGURE and in some cases of each other, will trigger different algorithms — different behaviors. Only with assertions (contracts) does the substitution idea make sense: the abstract behavior, as characterized by preconditions, postconditions and the class invariants, is the same (modulo respective weakening and strengthening to preserve the flexibility of the different version). Realizing this was a major step in understanding inheritance and typing.

I do not know of any earlier (or contemporary) exposition of this principle and it would be normal to get the appropriate recognition.

Software design: design patterns

Two of the important patterns in the “Gang of Four” Design Patterns book (GoF) by Gamma et al. (1995) are the Command Pattern and the Bridge Pattern. I introduced them (under different names) in the following publications:

• The command pattern appears in OOSC1 under the name “Undo-Redo” in section 12.2. The solution is essentially the same as in GoF. I do not know of any earlier exposition of the technique. See also notes [B] and [C].

• The bridge pattern appears under the name “handle technique” in my book Reusable Software: The Base Component Libraries (Prentice Hall, 1994). It had been described several years earlier in manuals for Eiffel libraries. I do not know of an earlier reference. (The second edition of Object-Oriented Software Construction — Prentice Hall, 1997, “OOSC2” –, which also describes it, states that a similar technique is described in an article by Josef Gil and Ricardo Szmit at the TOOLS USA conference in the summer of 1994, i.e. after the publication of Reusable Software.)

Note that it is pointless to claim precedence over GoF since that book explicitly states that it is collecting known “best practices”, not introducing new ones. The relevant questions are: who, pre-GoF, introduced each of these techniques first; and which publications does the GoF cites as “prior art”  for each pattern. In the cases at hand, Command and Bridge, it does not cite OOSC1.

To be concrete: unless someone can point to an earlier reference, then anytime anyone anywhere using an interactive system enters a few “CTRL-Z” to undo commands, possibly followed by some “CTRL-Y” to redo them (or uses other UI conventions to achieve these goals), the software most likely relying on a technique that I first described in the place mentioned above.

Software design: Open-Closed Principle

Another contribution of OOSC1 (1988), section 2.3, reinforced in OOSC2 (1997) is the Open-Closed principle, which explained one of the key aspects of inheritance: the ability to keep a module both closed (immediately usable as is) and open to extension (through inheritance, preserving the basic semantics. I am mentioning this idea only in passing since in this case my contribution is usually recognized, for example in the Wikipedia entry.

Software design: OO for reuse

Reusability: the Case for Object-Oriented Design (1987) is, I believe, the first publication that clearly explained why object-oriented concepts were (and still are today — in Grady Booch’s words, “there is no other game in town”) the best answer to realize the goal of software construction from software components. In particular, the article:

• Explains the relationship between abstract data types and OO programming, showing the former as the theoretical basis for the latter. (The CLU language at MIT originated from Liskov’s pioneering work on abstract data types, but was not OO in the full sense of the term, missing in particular a concept of inheritance.)
• Shows that reusability implies bottom-up development. (Top-down refinement was the mantra at the time, and promoting bottom-up was quite a shock for many people.)
• Explains the role of inheritance for reuse, as a complement to Parnas’s interface-based modular construction with information hiding.

Software design: Design by Contract

The contribution of Design by Contract is one that is widely acknowledged so I don’t have any point to establish here — I will just recall the essentials. The notion of assertion goes back to the work of Floyd, Hoare and Dijkstra in the sixties and seventies, and correctness-by-construction to Dijktra, Gries and Wirth, but Design by Contract is a comprehensive framework providing:

• The use of assertions in an object-oriented context. (The notion of class invariant was mentioned in a paper by Tony Hoare published back in 1972.)
• The connection of inheritance with assertions (as sketched above). That part as far as I know was entirely new.
• A design methodology for quality software: the core of DbC.
• Language constructs carefully seamed into the fabric of the language. (There were precedents there, but in the form of research languages such as Alphard, a paper design only, not implemented, and Euclid.)
• A documentation methodology.
• Support for testing.
• Support for a consistent theory of exception handling (see next).

Design by Contract is sometimes taken to mean simply the addition of a few assertions here and there. What the term actually denotes is a comprehensive methodology with all the above components, tightly integrated into the programming language. Note in particular that preconditions and postconditions are not sufficient; in an OO context class invariants are essential.

Software design: exceptions

Prior to the Design by Contract work, exceptions were defined very vaguely, as something special you do outside of “normal” cases, but without defining “normal”. Design by Contract brings a proper perspective by defining these concepts precisely. This was explained in a 1987 article, Disciplined Exceptions ([86] in the list), rejected by ECOOP but circulated as a technical report; they appear again in detail in OOSC1 (sections 7.10.3 to 7.10.5).

Other important foundational work on exceptions, to which I know no real precursor (as usual I would be happy to correct any omission), addressed what happens to the outcome of an exception in a concurrent or distributed context. This work was done at ETH, in particular in the PhD theses  of B. Morandi and A. Kolesnichenko, co-supervised with S. Nanz. See the co-authored papers [345] and [363].

On the verification aspect of exceptions, see below.

Software design: refactoring

I have never seen a discussion of refactoring that refers to the detailed discussion of generalization in both of the books Reusable Software (1994, chapter 3) and Object Success (Prentice Hall, 1995, from page 122 to the end of chapter 6). These discussions describe in detail how, once a program has been shown to work, it should be subject to a posteriori design improvements. It presents several of the refactoring techniques (as they were called when the idea gained traction several years later), such as moving common elements up in the class hierarchy, and adding an abstract class as parent to concrete classes ex post facto.

These ideas are an integral part of the design methodology presented in these books (and again in OOSC2 a few later). It is beyond me why people would present refactoring (or its history, as in the Wikipedia entry on the topic) without referring to these publications, which were widely circulated and are available for anyone to inspect.

Software design: built-in documentation and Single-Product principle

Another original contribution was the idea of including documentation in the code itself and relying on tools to extract the documentation-only information (leaving implementation elements aside). The idea, described in detail in OOSC1 in 1988 (sections 9.4 and 9.5) and already mentioned in the earlier Eiffel papers, is that code should be self-complete, containing elements of various levels of abstraction; some of them describe implementation, but the higher-level elements describe specification, and are distinguished syntactically in such a way that tools can extract them to produce documentation at any desired level of abstraction.

The ideas were later applied through such mechanisms as JavaDoc (with no credit as far as I know). They were present in Eiffel from the start and the underlying principles, in particular the “Single Product principle” (sometimes “Self-Documentation principle”, and also generalized by J. Ostroff and R. Paige as “Single-Model principle”). Eiffel is the best realization of these principles thanks to:

• Contracts (as mentioned above): the “contract view” of a class (called “short form” in earlier descriptions) removes the implementations but shows the relevant preconditions, postconditions and class invariants, given a precise and abstract specification of the class.
• Eiffel syntax has a special place for “header comments”, which describe high-level properties and remain in the contract view.
• Eiffel library class documentation has always been based on specifications automatically extracted from the actual text of the classes, guaranteeing adequacy of the documentation. Several formats are supported (including, from 1995 on, HTML, so that documentation can be automatically deployed on the Web).
• Starting with the EiffelCase tool in the early 90s, and today with the Diagram Tool of EiffelStudio, class structures (inheritance and client relationships) are displayed graphically, again in an automatically extracted form, using either the BON or UML conventions.

One of the core benefits of the Single-Product principle is to guard against what some of my publications called the “Dorian Gray” syndrome: divergence of an implementation from its description, a critical problem in software because of the ease of modifying stuff. Having the documentation as an integral part of the code helps ensure that when information at some level of abstraction (specification, design, implementation) changes, the other levels will be updated as well.

Crucial in the approach is the “roundtripping” requirement: specifiers or implementers can make changes in any of the views, and have them reflected automatically in the other views. For example, you can graphically draw an arrow between two bubbles representing classes B and A in the Diagram Tool, and the code of B will be updated with “inherit A”; or you can add this Inheritance clause textually in the code of class B, and the diagram will be automatically updated with an arrow.

It is important to note how contrarian and subversive these ideas were at the time of their introduction (and still to some extent today). The wisdom was that you do requirements then design then implementation, and that code is a lowly product entirely separate from specification and documentation. Model-Driven Development perpetuates this idea (you are not supposed to modify the code, and if you do there is generally no easy way to propagate the change to the model.) Rehabilitating the code (a precursor idea to agile methods, see below) was a complete change of perspective.

I am aware of no precedent for this Single Product approach. The closest earlier ideas I can think of are in Knuth’s introduction of Literate Programming in the early eighties (with a book in 1984). As in the Single-product approach, documentation is interspersed with code. But the literate programming approach is (as presented) top-down, with English-like explanations progressively being extended with implementation elements. The Single Product approach emphasizes the primacy of code and, in terms of the design process, is very much yoyo, alternating top-down (from the specification to the implementation) and bottom-up (from the implementation to the abstraction) steps. In addition, a large part of the documentation, and often the most important one, is not informal English but formal assertions. I knew about Literate Programming, of course, and learned from it, but Single-Product is something else.

Software design: from patterns to components

Karine Arnout’s thesis at ETH Zurich, resulting in two co-authored articles ([255] and [257], showed that contrary to conventional wisdom a good proportion of the classical design patterns, including some of the most sophisticated, can be transformed into reusable components (indeed part of an Eiffel library). The agent mechanism (see below) was instrumental in achieving that result.

Programming, design and specification concepts: abstract data types

Liskov’s and Zilles’s ground-breaking 1974 abstract data types paper presented the concepts without a mathematical specification, using programming language constructs instead. A 1976 paper (number [3] in my publication list, La Description des Structures de Données, i.e. the description of data structures) was as far as I know one of the first to present a mathematical formalism, as  used today in presentations of ADTs. John Guttag was taking a similar approach in his PhD thesis at about the same time, and went further in providing a sound mathematical foundation, introducing in particular (in a 1978 paper with Jim Horning) the notion of sufficient completeness, to which I devoted a full article in this blog  (Are My Requirements Complete?) about a year ago. My own article was published in a not very well known journal and in French, so I don’t think it had much direct influence. (My later books reused some of the material.)

The three-level description approach of that article (later presented in English for an ACM workshop in the US in 1981, Pingree Park, reference [28]) is not well known but still applicable, and would be useful to avoid frequent confusions between ADT specifications and more explicit descriptions.

When I wrote my 1976 paper, I was not aware of Guttag’s ongoing work (only of the Liskov and Zilles paper), so the use of a mathematical framework with functions and predicates on them was devised independently. (I remember being quite happy when I saw what the axioms should be for a queue.) Guttag and I both gave talks at a workshop organized by the French programming language interest group in 1977 and it was fun to see that our presentations were almost identical. I think my paper still reads well today (well, if you read French). Whether or not it exerted direct influence, I am proud that it independently introduced the modern way of thinking of abstract data types as characterized by mathematical functions and their formal (predicate calculus) properties.

Language mechanisms: genericity with inheritance

Every once in a while I get to referee a paper that starts “Generics, as introduced in Java…” Well, let’s get some perspective here. Eiffel from its introduction in 1985 combined genericity and inheritance. Initially, C++ users and designers claimed that genericity was not needed in an OO context and the language did not have it; then they introduced template. Initially, the designers of Java claimed (around 1995) that genericity was not needed, and the language did not have it; a few years later Java got generics. Initially, the designers of C# (around 1999) claimed that genericity was not needed, and the language did not have it; a few years later C# and .NET got generics.

Genericity existed before Eiffel of course; what was new was the combination with inheritance. I had been influenced by work on generic modules by a French researcher, Didier Bert, which I believe influenced the design of Ada as well; Ada was the language that brought genericity to a much broader audience than the somewhat confidential languages that had such a mechanism before. But Ada was not object-oriented (it only had modules, not classes). I was passionate about object-oriented programming (at a time when it was generally considered, by the few people who had heard of it as an esoteric, academic pursuit). I started — in the context of an advanced course I was teaching at UC Santa Barbara — an investigation of how the two mechanisms relate to each other. The results were a paper at the first OOPSLA in 1986, Genericity versus Inheritance, and the design of the Eiffel type system, with a class mechanism, inheritance (single and multiple), and genericity, carefully crafted to complement each other.

With the exception of a Trellis-Owl, a  design from Digital Equipment Corporation also presented at the same OOPSLA (which never gained significant usage), there were no other OO languages with both mechanisms for several years after the Genericity versus Inheritance paper and the implementation of genericity with inheritance in Eiffel available from 1986 on. Eiffel also introduced, as far as I know, the concept of constrained genericity, the second basic mechanism for combining genericity with inheritance, described in Eiffel: The Language (Prentice Hall, 1992, section 10.8) and discussed again in OOSC2 (section 16.4 and throughout). Similar mechanisms are present in many languages today.

It was not always so. I distinctly remember people bringing their friends to our booth at some conference in the early nineties, for the sole purpose of having a good laugh with them at our poster advertising genericity with inheritance. (“What is this thing they have and no one else does? Generi-sissy-tee? Hahaha.”). A few years later, proponents of Java were pontificating that no serious language needs generics.

It is undoubtedly part of of the cycle of invention (there is a Schopenhauer citation on this, actually the only thing from Schopenhauer’s philosophy that I ever understood [D]) that people at some point will laugh at you; if it did brighten their day, why would the inventor deny them one of the little pleasures of life? But in terms of who laughs last, along the way C++ got templates, Java got generics, C# finally did too, and nowadays all typed OO languages have something of the sort.

Language mechanisms: multiple inheritance

Some readers will probably have been told that multiple inheritance is a bad thing, and hence will not count it as a contribution, but if done properly it provides a major abstraction mechanism, useful in many circumstances. Eiffel showed how to do multiple inheritance right by clearly distinguishing between features (operations) and their names, defining a class as a finite mapping between names and features, and using renaming to resolve any name clashes.

Multiple inheritance was made possible by an implementation innovation: discovering a technique (widely imitated since, including in single-inheritance contexts) to implement dynamic binding in constant time. It was universally believed at the time that multiple inheritance had a strong impact on performance, because dynamic binding implied a run-time traversal of the class inheritance structure, already bad enough for single inheritance where the structure is a tree, but prohibitive with multiple inheritance for which it is a directed acyclic graph. From its very first implementation in 1986 Eiffel used what is today known as a virtual table technique which guarantees constant-time execution of routine (method) calls with dynamic binding.

Language mechanisms: safe GC through strong static typing

Simula 67 implementations did not have automatic garbage collection, and neither had implementations of C++. The official excuse in the C++ case was methodological: C programmers are used to exerting manual control of memory usage. But the real reason was a technical impossibility resulting from the design of the language: compatibility with C precludes the provision of a good GC.

More precisely, of a sound and complete GC. A GC is sound if it will only reclaim unreachable objects; it is complete if it will reclaim all unreachable objects. With a C-based language supporting casts (e.g. between integers and pointers) and pointer arithmetic, it is impossible to achieve soundness if we aim at a reasonable level of completeness: a pointer can masquerade as an integer, only to be cast back into a pointer later on, but in the meantime the garbage collector, not recognizing it as a pointer, may have wrongly reclaimed the corresponding object. Catastrophe.

It is only possible in such a language to have a conservative GC, meaning that it renounces completeness. A conservative GC will treat as a pointer any integer whose value could possibly be a pointer (because it lies between the bounds of the program’s data addresses in memory). Then, out of precaution, the GC will refrain from reclaiming the objects at these addresses even if they appear unreachable.

This approach makes the GC sound but it is only a heuristics, and it inevitably loses completeness: every once in a while it will fail to reclaim some dead (unreachable) objects around. The result is a program with memory leaks — usually unacceptable in practice, particularly for long-running or continuously running programs where the leaks inexorably accumulate until the program starts thrashing then runs out of memory.

Smalltalk, like Lisp, made garbage collection possible, but was not a typed language and missed on the performance benefits of treating simple values like integers as a non-OO language would. Although in this case I do not at the moment have a specific bibliographic reference, I believe that it is in the context of Eiffel that the close connection between strong static typing (avoiding mechanisms such as casts and pointer arithmetic) and the possibility of sound and complete garbage collection was first clearly explained. Explained in particular around 1990 in a meeting with some of the future designers of Java, which uses a similar approach, also taken over later on by C#.

By the way, no one will laugh at you today for considering garbage collection as a kind of basic human right for programmers, but for a long time the very idea was quite sulfurous, and advocating it subjected you to a lot of scorn. Here is an extract of the review I got when I submitted the first Eiffel paper to IEEE Transactions on Software Engineering:

Systems that do automatic garbage collection and prevent the designer from doing his own memory management are not good systems for industrial-strength software engineering.

Famous last words. Another gem from another reviewer of the same paper:

I think time will show that inheritance (section 1.5.3) is a terrible idea.

Wow! I wish the anonymous reviewers would tell us what they think today. Needless to say, the paper was summarily rejected. (It later appeared in the Journal of Systems and Software — as [82] in the publication list — thanks to the enlightened views of Robert Glass, the founding editor.)

Language mechanisms: void safety

Void safety is a property of a language design that guarantees the absence of the plague of null pointer dereferencing.

The original idea came (as far as I know) from work at Microsoft Research that led to the design of a research language called C-omega; the techniques were not transferred to a full-fledged programming language. Benefiting from the existence of this proof of concept, the Eiffel design was reworked to guarantee void safety, starting from my 2005 ECOOP keynote paper (Attached Types) and reaching full type safety a few years later. This property of the language was mechanically proved in a 2016 ETH thesis by A. Kogtenkov.

Today all significant Eiffel development produces void-safe code. As far as I know this was a first among production programming languages and Eiffel remains the only production language to provide a guarantee of full void-safety.

This mechanism, carefully crafted (hint: the difficult part is initialization), is among those of which I am proudest, because in the rest of the programming world null pointer dereferencing is a major plague, threatening at any moment to crash the execution of any program that uses pointers of references. For Eiffel users it is gone.

Language mechanisms: agents/delegates/lambdas

For a long time, OO programming languages did not have a mechanism for defining objects wrapping individual operations. Eiffel’s agent facility was the first such mechanism or among the very first together the roughly contemporaneous but initially much more limited delegates of C#. The 1999 paper From calls to agents (with P. Dubois, M. Howard, M. Schweitzer and E. Stapf, [196] in the list) was as far as I know the first description of such a construct in the scientific literature.

Language mechanisms: concurrency

The 1993 Communications of the ACM paper on Systematic Concurrent Object-Oriented Programming [136] was certainly not the first concurrency proposal for OO programming (there had been pioneering work reported in particular in the 1987 book edited by Tokoro and Yonezawa), but it innovated in offering a completely data-race-free model, still a rarity today (think for example of the multi-threading mechanisms of dominant OO languages).

SCOOP, as it came to be called, was implemented a few years later and is today a standard part of Eiffel.

Language mechanisms: selective exports

Information hiding, as introduced by Parnas in his two seminal 1972 articles, distinguishes between public and secret features of a module. The first OO programming language, Simula 67, had only these two possibilities for classes and so did Ada for modules.

In building libraries of reusable components I realized early on that we need a more fine-grained mechanism. For example if class LINKED_LIST uses an auxiliary class LINKABLE to represent individual cells of a linked list (each with a value field and a “right” field containing a reference to another LINKABLE), the features of LINKABLE (such as the operation to reattach the “right” field) should not be secret, since LINKED_LIST needs them; but they should also not be generally public, since we do not want arbitrary client objects to mess around with the internal structure of the list. They should be exported selectively to LINKED_LIST only. The Eiffel syntax is simple: declare these operations in a clause of the class labeled “feature {LINKED_LIST}”.

This mechanism, known as selective exports, was introduced around 1989 (it is specified in full in Eiffel: The Language, from 1992, but was in the Eiffel manuals earlier). I think it predated the C++ “friends” mechanism which serves a similar purpose (maybe someone with knowledge of the history of C++ has the exact date). Selective exports are more general than the friends facility and similar ones in other OO languages: specifying a class as a friend means it has access to all your internals. This solution is too coarse-grained. Eiffel’s selective exports make it possible to define the specific export rights of individual operations (including attributes/fields) individually.

Language mechanisms and implementation: serialization and schema evolution

I did not invent serialization. As a student at Stanford in 1974 I had the privilege, at the AI lab, of using SAIL (Stanford Artificial Intelligence Language). SAIL was not object-oriented but included many innovative ideas; it was far ahead of its time, especially in terms of the integration of the language with (what was not yet called) its IDE. One feature of SAIL with which one could fall in love at first sight was the possibility of selecting an object and having its full dependent data structure (the entire subgraph of the object graph reached by following references from the object, recursively) stored into a file, for retrieval at the next section. After that, I never wanted again to live without such a facility, but no other language and environment had it.

Serialization was almost the first thing we implemented for Eiffel: the ability to write object.store (file) to have the entire structure from object stored into file, and the corresponding retrieval operation. OOSC1 (section 15.5) presents these mechanisms. Simula and (I think) C++ did not have anything of the sort; I am not sure about Smalltalk. Later on, of course, serialization mechanisms became a frequent component of OO environments.

Eiffel remained innovative by tackling the difficult problems: what happens when you try to retrieve an object structure and some classes have changed? Only with a coherent theoretical framework as provided in Eiffel by Design by Contract can one devise a meaningful solution. The problem and our solutions are described in detail in OOSC2 (the whole of chapter 31, particularly the section entitled “Schema evolution”). Further advances were made by Marco Piccioni in his PhD thesis at ETH and published in joint papers with him and M. Oriol, particularly [352].

Language mechanisms and implementation: safe GC through strong static typing

Simula 67 (if I remember right) did not have automatic garbage collection, and neither had C++ implementations. The official justification in the case of C++ was methodological: C programmers are used to exerting manual control of memory usage. But the real obstacle was technical: compatibility with C makes it impossible to have a good GC. More precisely, to have a sound and complete GC. A GC is sound if it will only reclaim unreachable objects; it is complete if it will reclaim all unreachable objects. With a C-based language supporting casts (e.g. between integers and pointers) and pointer arithmetic, it is impossible to achieve soundness if we aim at a reasonable level of completeness: a pointer can masquerade as an integer, only to be cast back into a pointer later on, but in the meantime the garbage collector, not recognizing it as a pointer, may have wrongly reclaimed the corresponding object. Catastrophe. It is only possible in such a language to have a conservative GC, which will treat as a pointer any integer whose value could possibly be a pointer (because its value lies between the bounds of the program’s data addresses in memory). Then, out of precaution, it will not reclaim the objects at the corresponding address. This approach makes the GC sound but it is only a heuristics, and it may be over-conservative at times, wrongly leaving dead (i.e. unreachable) objects around. The result is, inevitably, a program with memory leaks — usually unacceptable in practice.

Smalltalk, like Lisp, made garbage collection possible, but was not a typed language and missed on the performance benefits of treating simple values like integers as a non-OO language would. Although in this case I do not at the moment have a specific bibliographic reference, I believe that it is in the context of Eiffel that the close connection between strong static typing (avoiding mechanisms such as casts and pointer arithmetic) and the possibility of sound and complete garbage collection was first clearly explained. Explained in particular to some of the future designers of Java, which uses a similar approach, also taken over later on by C#.

By the way, no one will laugh at you today for considering garbage collection as a kind of basic human right for programmers, but for a long time it was quite sulfurous. Here is an extract of the review I got when I submitted the first Eiffel paper to IEEE <em>Transactions on Software Engineering:

Software engineering: primacy of code

Agile methods are widely and properly lauded for emphasizing the central role of code, against designs and other non-executable artifacts. By reading the agile literature you might be forgiven for believing that no one brought up that point before.

Object Success (1995) makes the argument very clearly. For example, chapter 3, page 43:

Code is to our industry what bread is to a baker and books to a writer. But with the waterfall code only appears late in the process; for a manager this is an unacceptable risk factor. Anyone with practical experience in software development knows how many things can go wrong once you get down to code: a brilliant design idea whose implementation turns out to require tens of megabytes of space or minutes of response time; beautiful bubbles and arrows that cannot be implemented; an operating system update, crucial to the project which comes five weeks late; an obscure bug that takes ages to be fixed. Unless you start coding early in the process, you will not be able to control your project.

Such discourse was subversive at the time; the wisdom in software engineering was that you need to specify and design a system to death before you even start coding (otherwise you are just a messy “hacker” in the sense this word had at the time). No one else in respectable software engineering circles was, as far as I know, pushing for putting code at the center, the way the above extract does.

Several years later, agile authors started making similar arguments, but I don’t know why they never referenced this earlier exposition, which still today I find not too bad. (Maybe they decided it was more effective to have a foil, the scorned Waterfall, and to claim that everyone else before was downplaying the importance of code, but that was not in fact everyone.)

Just to be clear, Agile brought many important ideas that my publications did not anticipate; but this particular one I did.

Software engineering: the roles of managers

Extreme Programming and Scrum have brought new light on the role of managers in software development. Their contributions have been important and influential, but here too they were for a significant part prefigured by a long discussion, altogether two chapters, in Object Success (1995).

To realize this, it is enough to read the titles of some of the sections in those chapters, describing roles for managers (some universal, some for a technical manager): “risk manager”, “interface with the rest of the world” (very scrummy!), “protector of the team’s sanity”, “method enforcer” (think Scrum Master), “mentor and critic”. Again, as far as I know, these were original thoughts at the time; the software engineering literature for the most part did not talk about these issues.

Software engineering: outsourcing

As far as I know the 2006 paper Offshore Development: The Unspoken Revolution in Software Engineering was the first to draw attention, in the software engineering community, to the peculiar software engineering challenges of distributed and outsourced development.

Software engineering: automatic testing

The AutoTest project (with many publications, involving I. Ciupa, A. Leitner, Y. Wei, M. Oriol, Y. Pei, M. Nordio and others) was not the first to generate tests automatically by creating numerous instances of objects and calling applicable operations (it was preceded by Korat at MIT), but it was the first one to apply this concept with Design by Contract mechanisms (without which it is of little practical value, since one must still produce test oracles manually) and the first to be integrated in a production environment (EiffelStudio).

Software engineering: make-less system building

One of the very first decisions in the design of Eiffel was to get rid of Make files.

Feldman’s Make had of course been a great innovation. Before Make, programmers had to produce executable systems manually by executing sequences of commands to compile and link the various source components. Make enabled them to instead  to define dependencies between components in a declarative way, resulting in a partial order, and then performed a topological sort to produce the sequence of comments. But preparing the list of dependencies remains a tedious task, particularly error-prone for large systems.

I decided right away in the design of Eiffel that we would never force programmers to write such dependencies: they would be automatically extracted from the code, through an exhaustive analysis of the dependencies between modules. This idea was present from the very the first Eiffel report in 1985 (reference [55] in the publication list): Eiffel programmers never need to write a Make file or equivalent (other than for non-Eiffel code, e.g. C or C++, that they want to integrate); they just click a Compile button and the compiler figures out the steps.

Behind this approach was a detailed theoretical analysis of possible relations between modules in software development (in many programming languages), published as the “Software Knowledge Base” at ICSE in 1985. That analysis was also quite instructive and I would like to return to this work and expand it.

Educational techniques: objects first

Towards an Object-Oriented Curriculum ( TOOLS conference, August 1993, see also the shorter JOOP paper in May of the same year) makes a carefully argued case for what was later called the Objects First approach to teaching programming. I would be interested to know if there are earlier publications advocating starting programming education with an OO language.

The article also advocated for the “inverted curriculum”, a term borrowed from work by Bernie Cohen about teaching electrical engineering. It was the first transposition of this concept to software education. In the article’s approach, students are given program components to use, then little by little discover how they are made. This technique met with some skepticism and resistance since the standard approach was to start from the very basics (write trivial programs), then move up. Today, of course, many introductory programming courses similarly provide students from day one with a full-fledged set of components enabling them to produce significant programs.

More recent articles on similar topics, taking advantage of actual teaching experience, are The Outside-In Method of Teaching Programming (2003) and The Inverted Curriculum in Practice (at ICSE 2006, with Michela Pedroni). The culmination of that experience is the textbook Touch of Class from 2009.

Educational techniques: Distributed Software Projects

I believe our team at ETH Zurich (including among others M. Nordio, J. Tschannen, P. Kolb and C. Estler and in collaboration with C. Ghezzi, E. Di Nitto and G. Tamburrelli at Politecnico di Milano, N. Aguirre at Rio Cuarto and many others in various universities) was the first to devise,  practice and document on a large scale (see publications and other details here) the idea of an educational software project conducted in common by student groups from different universities. It yielded a wealth of information on distributed software development and educational issues.

Educational techniques: Web-based programming exercises

There are today a number of cloud-based environments supporting the teaching of programming by enabling students to compile and test their programs on the Web, benefiting from a prepared environment (so that they don’t have to download any tools or prepare control files) and providing feedback. One of the first — I am not sure about absolute precedence — and still a leading one, used by many universities and applicable to many programming languages, is Codeboard.

The main developer, in my chair at ETH Zurich, was Christian Estler, supported in particular by M. Nordio and M. Piccioni, so I am only claiming a supporting role here.

Educational techniques: key CS/SE concepts

The 2001 paper Software Engineering in the Academy did a good job, I think, of defining the essential concepts to teach in a proper curriculum (part of what Jeannette Wing’s 2006 paper called Computational Thinking).

Program verification: agents (delegates etc.)

Reasoning about Function Objects (ICSE 2010, with M. Nordio, P. Müller and J. Tschannen) introduced verification techniques for objects representing functions (such as agents, delegates etc., see above) in an OO language. Not sure whether there were any such techniques before.

Specification languages: Z

The Z specification language has been widely used for formal development, particularly in the UK. It is the design of J-R Abrial. I may point out that I was a coauthor of the first publication on Z in English (1980),  describing a version that preceded the adaptation to a more graphical-style notation done later at Oxford. The first ever published description of Z, pertaining to an even earlier version, was in French, in my book Méthodes de Programmation (with C. Baudoin), Eyrolles, 1978, running over 15 pages (526-541), with the precise description of a refinement process.

Program verification: exceptions

Largely coming out of the PhD thesis of Martin Nordio, A Sound and Complete Program Logic for Eiffel (TOOLS 2009) introduces rules for dealing with exceptions in a Hoare-style verification framework.

Program verification: full library, and AutoProof

Nadia Polikarpova’s thesis at ETH, aided by the work of Carlo Furia and Julian Tschannen (they were the major contributors and my participation was less important), was as far as I know the first to produce a full functional verification of an actual production-quality reusable library. The library is EiffelBase 2, covering fundamental data structures.

AutoProof — available today, as a still experimental tool, through its Web interface, see here — relied on the AutoProof prover, built by the same team, and itself based on Microsoft Research’s Boogie and Z3 engines.

More

There are more concepts worthy of being included here, but for today I will stop here.

Notes

[A] One point of divergence between usual presentations of the substitution principle and the view in OOSC and my other publications is the covariance versus contravariance of routine argument types. It reflects a difference of views as to what the proper policy (both mathematically sound and practically usable) should be.

[B]  The GoF book does not cite OOSC for the command or bridge patterns. For the command pattern it cites (thanks to Adam Kosmaczewski for digging up the GoF text!) a 1985 SIGGRAPH paper by Henry Lieberman (There’s More to Menu Systems than Meets the Screen). Lieberman’s paper describes the notion of command object and mentions undoing in passing, but does not include the key elements of the command pattern (as explained in full in OOSC1), i.e. an abstract (deferred) command class with deferred procedures called (say) do_it and undo_it, then specific classes for each kind of command, each providing a specific implementation of those procedures, then a history list of commands supporting multiple-level undo and redo as explained in OOSC1. (Reading Lieberman’s paper with a 2021 perspective shows that it came tantalizingly close to the command pattern, but doesn’t get to it. The paper does talk about inheritance between command classes, but only to “define new commands as extensions to old commands”, not in the sense of a general template that can be implemented in many specific ways. And it does mention a list of objects kept around to enable recovery from accidental deletions, and states that the application can control its length, as is the case with a history list; but the objects in the list are not command objects, they are graphical and other objects that have been deleted.)

[C] Additional note on the command pattern: I vaguely remember seeing something similar to the OOSC1 technique in an article from a supplementary volume of the OOPSLA proceedings in the late eighties or early nineties, i.e. at the same time or slightly later, possibly from authors from Xerox PARC, but I have lost the reference.

[D] Correction: I just checked the source and learned that the actual Schopenhauer quote (as opposed to the one that is usually quoted) is different; it does not include the part about laughing. So much for my attempts at understanding philosophy.

Let us assume for the sake of the argument that software quality matters. There are many ingredients to software quality, of which one must be the care that every programmer devotes to the job. The Personal Software Process, developed by Watts Humphrey in the 1990s [1], prescribes a discipline that software developers should apply to produce good software and improve their professional ability over their careers. It has enjoyed moderate success but was never a mass movement and rarely gets mentioned nowadays; few software developers, in my experience, even know the name. Those who do often think of it as passé, a touching memory from the era of Monica Lewinsky and the Roseanne show.

Once cleaned of a few obsolete elements, PSP deserves to be known and applied.

PSP came out of Watts Humphrey’s earlier work on the Capability Maturity Model (see my earlier article on this blog, What is wrong with CMMI), a collection of recommended practices and assessment criteria for software processes, originally developed in the mid-eighties for the U.S. military contractor community but soon thereafter embraced by software outsourcing companies (initially, Indian ones) and later by other industries. Responding to complaints that CMM/CMMI, focused on processes in large companies, ignored the needs of smaller ones, and lacked individual guidance for developers, Humphrey developed TSP, the Team Software Process, and PSP.

The most visible part of PSP is a six-step process pictured in the middle of this diagram:

The most visible and also the most corny. Who today wants to promise always to follow such a strict sequence of steps? Always to write the code for a module in full before compiling it? (Notice there is no backward arrow, the process is sequential.) Always to test at the end only? Come on. This is the third decade of the 21st century.

Today we compile as we code, using the development environment (IDE) as a brilliant tool to check everything we do or plan to do. For my part, whenever I am writing code and have not compiled my current draft for more than a few minutes I start feeling like an addict in need of a fix; my fix is the Compile button of EiffelStudio. At some eventual stage the compiler becomes a tool to generate excutable code, but long before that it has been my friend, coach, mentor, and doppelgänger, helping me get things (types, null references, inheritance…) right and gently chiding me when I wander off the rails.

As to tests, even if you do not buy into the full dogma of Test-Driven Development (I don’t), they get written and exercised right from the start, as you are writing the code, not afterwards. Compile all the time, test all the time.

It’s not just that a process such as the above ignores the contributions of agile methods, which are largely posterior to PSP. As analyzed in [2], agile is a curious mix of good ideas and a few horrendous ones. But among its durable contributions is the realization that development must be incremental, not a strict succession of separate activities.

This old-style flavor or PSP is probably the reason why it has fallen out of favor. But (like the agile rejection of upfront lifecycle activities) such a reaction is a case of criticism gone too far, ignoring the truly beneficial contributions. Ignore PSP’s outmoded sequence of activities and you will find that PSP’s core message is as relevant today as it ever was. That message is: we should learn from the practices of traditional engineers and apply a strict professional discipline. For example:

• Keep a log of all activities. (See “Logs” in the above figure.) Engineers are taught to record everything they do; many programmers don’t bother. This practice, however, is essential to self-improvement.
• Keep measurements of everything you do. (There are lots of things to measure, from hours spent on every kind of task to bugs found, time to fix them etc.)
• Estimate and plan your work.
• Clearly define commitments, and meet them.
• Resist pressure to make unreasonable commitments (something that agilists approach also emphasize).
• Understand your current performance.
• Understand your programming style and how it affects various measures. (As an example, code size, as a function of the number of routines, depends on whether you are more concise or more verbose in style).
• Continually improve your expertise as a professional.

PSP does not limit itself to such exhortations but gives concrete tools to apply the principles, with a view to: measuring, tracking and analyzing your work; learning from your performance variations; and incorporating the lessons learned into your professional practices. On the topic of measurement, for example, PSP includes precise guidelines on what to measure and how to measure it, and how to rely on proxies for quantities that are hard to assess directly. On this last point, PSP includes PROBE (PROxy-Based Estimating, you cannot have a method coming out of the world of US government organizations without cringeworthy acronyms), a general framework for estimating size and resource parameters from directly measurable proxies.

This is what PSP is about: a discipline of personal productivity and growth, emphasizing personal discipline, tracking and constant improvement. It is not hard to learn; a technical report by Humphrey available online [3] provides a sufficient basis to understand the concepts and start a process of self-improvement.

Watts Humphrey himself, as all who had the privilege to meet him can testify, was a model of seriousness and professionalism, the quintessential engineer. (I also remember him as the author of what may be the best pun I ever heard — ask me sometime.) PSP directly reflects these qualities and — ignoring its visible but in the end unimportant remnants from outdated technical choices — should be part of every software engineering curriculum and every software engineer’s collection of fundamental practices.

References

[1] Watts Humphrey, Introduction to the Personal Software Process, Addison-Wesley, 1996.

[2] Bertrand Meyer: Agile! The Good, the Hype and the Ugly, Springer, 2014, see here.

[3] Watts Humphrey, The Personal Software Process, Software Engineering Institute Technical Report CMU/SEI-2000-TR-022, available (in PDF, free) here.

A version of this article was first published in the Communications of the ACM blog.

.

If you want to know whether your_string has at least one upper-case character, you will write this in Eiffel:

if  ∃ c: your_string ¦ c.is_upper then …

Such predicate-calculus boolean expressions, using a quantifier ∀ (“for all”) or ∃ (“there exists”) are becoming common in Eiffel code. They are particularly useful in Design by Contract assertions, making it possible to characterize deep semantic properties of the code and its data structures. For example a class invariant clause in a class I wrote recently states

from_lists_exist: ∀ tf: triples_from ¦ tf ≠ Void                        — [1]

meaning that all the elements, if any, of the list triples_from  are non-void (non-null). The notation is the exact one from mathematics. (Mathematical notation sometimes uses a dot in place of the bar, but the bar is clearer, particularly in an OO context where the dot has another use.)

Programming languages should support time-honored notations from mathematics. Reaching this goal has been a driving force in the evolution of Eiffel, but not as a concession to “featurism” (the gratuitous piling up of language feature upon feature). The language must remain simple and consistent; any new feature must find its logical place in the overall edifice.

The design of programming languages is a constant search for the right balance between rigor, simplicity, consistency, formal understanding, preservation of existing code, innovation and expressiveness. The design of Eiffel has understood the last of these criteria as implying support for established notations from mathematics, not through feature accumulation but by re-interpreting these notations in terms of the language’s fundamental concepts. A typical example is the re-interpretation of the standard mathematical notation a + b as as simply an operator-based form for the object-oriented call a.plus (b), obtained by declaring “+” as an operator alias for the function plus in the relevant classes. There are many more such cases in today’s Eiffel. Quantifier expressions using ∀ and ∃ are the latest example.

 They are not a one-of-a-kind trick but just as a different syntax form for loops. Expressed in a more verbose form, the only one previously available, [1] would be:

across triples_from is tf all tf /= Void end                         — [2]

It is interesting to walk back the history further. [2] is itself a simplification of

across triples_from as tf all tf.item /= Void end               — [3]

where the “.item” has a good reason for being there, but that reason is irrelevant to a beginner. The earlier use of as in [3] is also the reason for the seemingly bizarre use of is in [2], which is only explainable by the backward compatibility criterion (code exists that uses as , which has a slightly different semantics from is), and will go away. But a few years ago the across loop variant did not exist and you would have had to write the above boolean expressions as

all_non_void (triples_from)

after defining a function

all_non_void (l: LIST [T]): BOOLEAN                                    — [4]
                         — Are all the elements of `l’, if any, non-void?
          local
pos: INTEGER
do
from
pos := l.index
l.start
Result := True
until not Result or l.after loop
l.forth
end
go_ith (pos)
end

The road traveled from [4] to [1] is staggering. As we introduced new notations in the history of Eiffel the reaction of the user community has sometimes been between cautious and negative. With the exception of a couple of quickly discarded ideas (such as the infamous and short-lived “!!” for creation), they were generally adopted widely because they simplify people’s life without adding undue complexity to the language. The key has been to avoid featurism and choose instead to provide two kinds of innovation:

• Major conceptual additions, which elevate the level of abstraction of the language. A typical introduction was the introduction of agents, which provide the full power of functional programming in an object-oriented context; another was the SCOOP concurrency mechanism. There have been only a few such extensions, all essential.
• Syntactical variants for existing concepts, allowing more concise forms obtained from traditional mathematical notation. The use of quantifier expressions as in [1] is the latest example.

Complaints of featurism still occasionally happen when people first encounter the new facilities, but they fade away quickly as people start using them. After writing a few expressions such as [1], no one wants to go back to any of the other forms.

These quantifier expressions using ∀ and ∃, as well as the “≠” not-equal sign for what used to be (and still commonly is) written “/=”, rely on Unicode. Eiffel started out when ASCII was the law of the land. (Or 8-bit extended ASCII, which does not help much since the extensions are rendered differently in different locales, i.e. the same 8-bit character code may mean something different on French and Swedish texts.) In recent years, Eiffel has made a quiet transition to full Unicode support. (Such support extends to manifest strings and operators, not to identifiers. The decision, which could be revisited, has been to keep the ASCII-only  policy for identifiers to favor compatible use by programmers regardless of their mother tongues.) The use of Unicode considerably extends the expressive power of the language, in particular for scientific software which can — thanks to Eiffel’s mechanism for defining free operators — rely on advanced mathematical notations.

Unicode is great, but I hear the question: how in the world can we enter the corresponding symbols, since our keyboards are still ASCII plus some extensions?

It would be tedious to have to select from a list of special symbols (as you do when inserting a mathematical symbol in Microsoft Word or, for that matter, as I did when inserting the phrase “∀ and ∃” in the preceding paragraph using WordPress).

The answer lies in the interplay between the language and the development environment. EiffelStudio, like other modern IDEs, includes an automatic completion mechanism which lets you enter the beginning of a construct and will take care of filling in the rest. Already useful for complex structures (if you type “if” the tools will create the entire “if … then … else … end” conditional structure for you to fill in), automatic completion will take care of inserting the appropriate Unicode symbols for you. Type for example “across”,  then CTRL-Space to trigger completion, and the choices will include the “∀” and “∃” forms. You can see below how this works:

Programming languages can be at the same time simple, easy to learn, consistent, and expressive. Start using quantifiers now!

Acknowledgments to the Ecma Technical Committee on Eiffel and the Eiffel Software team, particularly Alexander Kogtenkov (see his blog post here) and (for the completion mechanism and its animated illustration above) Jocelyn Fiat.

A group of us is preparing a survey on systems that have been both formally verified and deployed for actual use. To make sure we do not forget any important development, we have devised a questionnaire. If you have experience with such a system, please help by filling the questionnaire. It only includes a few questions and takes a few minutes to fill. You can find it here.

Please also bring it to the attention of others who might have relevant information.

Thanks in advance!

I have started a new series of video lectures, which I call “Meyer’s Object-Oriented Classes” (MOOC). The goal is to share insights I have gained over the years on various aspects of programming and software engineering. Many presentations are focused on one area, such as coding, design, analysis, theoretical computer science (even there you find a division between “Theory A”, i.e. complexity, Turing machines and the like, and “Theory B”, i.e. semantics, type theory etc.), software project management, concurrency… I have an interest in all and try to explain connections.

The first lecture describes the edit distance (Levenshtein) algorithm, explains its correctness by introducing the loop invariant, expands on that notion, then shows a recursive version, explores the connection with the original version (it’s the invariant), and probes further into another view of recursive computations, leading to the concept of dynamic programming.

The videos are on YouTube and can be accessed from bertrandmeyer.com/levenshtein. (The general page for all lectures is at bertrandmeyer.com/mooc.)

The lecture is recorded in four segments of about 15 minutes each. In the future I will limit myself to 8-10 minutes. In fact I may record this lecture again; for example it would be better if I had a live audience rather than talking to my screen, and in general the recording is somewhat low-tech, but circumstances command. Also, I will correct a few hiccups (at some point in the recording I notice a typo on a slide and fix it on the fly), but the content will remain the same.

Feedback is of course welcome. I hope to record about a lecture a week from now on.