Mathematics is not a game of hit and miss
I was recently looking at the math exercises of a 14-year-old, having to do with quadratic (second-degree) equations.
The first thing that caught my eye is not a surprise: the difference between school and life. The quadratic polynomials appearing in the exercises, such as x2 – x – 6, all happen to have integer roots (3 and -2 in this case). Also, they all have 1 as the second-degree coefficient (the `a’ in a x2 + b x + c). There are good pedagogical reasons for these choices: with more general parameters, solving the equation becomes a task of numerical computation, which has no connection to the topic. But in any real-life application (say, the computation of where a ball thrown into the air will hit the ground) the solution will not come ready-made as in these school exercises.
I found one of the exercises very good. It reads this way (this is a Zurich school, I am translating from the German): A pencil factory has two machines. To produce 100 pencils, the older machine would take 10 minutes more than both machines running together. If in a minute the newer machine produces 32 pencils, how many does the older one produce in the same time? It provides a good opportunity to practice how to model a problem by defining the appropriate mathematical parameters. Then — surprise — you get a quadratic equation whose solutions — surprise — are integers (only one of which makes sense). Useful gymnastics.
Another interesting example is the equation
Interesting because if you do not use a bit of insight you will not get anywhere; after all, there is a range of 4 for the exponents (from -1 for the square root to 0 for the constants, 1 for the terms in x, and 2 for the terms in x2), so squaring both sides to get rid of the square root, for example, would be hopeless. Now if you remember that this exercise goes with a lecture about 2nd-degree equations and apply what you have learned about them, you get the roots of the polynomial in the denominator on the left, x2 – x – 6, and can rewrite it as (x – 3) (x + 2). Then you notice that x – 3 also appears, multiplied by 5, in the right-side denominator; so you remove it on both sides, and from then it is all downhill: you get another quadratic equation which — surprise — has simple roots.
Throughout these exercises I see, introduced from the start, an idea that not all people having learned quadratic equations remember: the rule that any second-degree polynomial a x2 + b x + c can be written a (x – x0) (x – x1) where x0 and x1 are the roots (including when they are the same). It is often useful to turn such a polynomial into this form (particularly simple when a = 1).
Then I probed further and asked the student what he would do if the roots were not such simple integers. It turns out that he had no idea since that is not something they are taught at that level! They have not heard about the notion of determinant (b2 – 4 a c), and how it gives the solutions, through the standard formula: (-b ± d) / 2 a where d is the square root of the determinant.
I realized that the way they are taught to “solve” the equation (I have to put the word in quotes) is to try to guess some integer values that will make x2 + b x + c (good thing that a = 1 for all the examples!) zero. Specifically, you try out values u and v whose product is c and check whether (x – u) (x – v) works out to the given polynomial. If not, you continue guessing values until you find a pair that works. Mathematics as a game of hit-and-miss.
In the x2 – x – 6 example, let’s see… -3 and +2? Oh no, they do not fit. 1 and -6? Bummer. 6 and -1? Also not. Maybe -2 and +3? Bingo!
This method of poking around until you find something that clicks seems to me a strange thing to teach. I should include a caveat here: I am not an expert in mathematical pedagogy (and not even a mathematician). So I am asking questions, not passing judgment. Also, the place being Switzerland, where processes are usually thought out carefully, especially in education, I have to assume that whoever designed this curriculum had some hunch of what he was doing. But the result is puzzling. The kind of mathematics that helps people (and on which today’s world rests, whether directly or through physics and computer science) is not about guessing results. It is about establishing rules, in the form of axioms and theorems, proving the latter (from the former), and then relying on them to derive whatever specific results you need. The edifice of rules has a deep and elaborate structure, devised over centuries by giants standing on the shoulders of giants standing on the shoulders of other giants. But once you have a rule you no longer have to go to the underlying layers; you directly use the result of the combined work of countless smart people. It does not matter how many times they tried to derive them and how many mistakes they made along the way: their work has been vetted many times, and you can use its outcome in full confidence.
If I use my guessing powers to try values that might make a x2 + b x + c zero, I will succeed once in a while, particularly for schoolbook exercises. When I do not succeed, I have no clue whether the reason is my insufficient intellectual agility, the absence of simple solutions (integers or simple fractions), or the absence of any solution (students at the level under consideration have not heard of imaginary numbers yet). If I learn the formula (meaning, with a good teacher, not only learning it as a recipe but discovering why the recipe works), I am equipped to solve any quadratic equation, with or without simple integer solutions. When solving such equations I do not need to apply ingenuity to guess solutions, a remarkably pointless exercise (except maybe the first few times). I can reserve my ingenuity to more interesting pursuits.
Indeed there would be so much more to teach. I looked at the textbook with its many pages of examples of quadratic equation to solve; more accurately, to guess. All piecemeal, example by example; no attempt at generality (isn’t the quest for general results one of the prime characteristics of the mathematical spirit?) They are not even taught that sometimes there are no solutions among the numbers they know; good luck to the enterprising student who, having found the roots of x2 – x – 6 through the recommended approach of trial and error, confidently embarks on solving x2 – x + 6 = 0 (it is almost the same and so cannot be much harder, right?).
All that space and student attention are wasted at the expense of the theoretical and practical properties of quadratic equations, second-degree polynomials and parabolas. We could direct students to web sites such as this one where they can play with parabolas, try different parameters and animate the results. We could explain how quadratic equations serve as a fundamental tool for computing trajectories of projectiles. We could even introduce the notion of parabolic mirror and its very practical benefit following from a basic geometrical property. And we could put all this into a form that a 14-year-old will readily understand.
Mathematics is not just about applications. I also feel sorry that these children, by just being shown haphazard tricks, miss the sheer beauty of the underlying ideas, which struck many of us when we learned them at the same age. What a pity.
There may be a grand plan behind the way these topics get taught, but I do not see it. I only see an approach that seems poised to drill into young minds the conviction that mathematics is but a sad, boring and pointless game of tricks.
Thanks to Manuel Oriol for useful observati9ns.
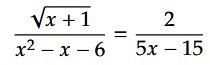
 Informatics Europe
Informatics Europe LASER summer school
LASER summer school Propulsion Academy
Propulsion Academy