Bertrand Meyer's technology+ blog

One of the occupational hazards of spreading the word about Eiffel is the frequent answer “yes, it’s much better than the language I use now, I would like to switch, but…“, followed by some sheepish excuse.

Last night I went to see Eugene Onegin once more (I still hope some day to land the part of Monsieur Triquet). Towards the beginning of the first act [1], Tatiana’s mother (Larina), reflecting in a melancholic tone on the vicissitudes of her (long ago) arranged marriage (and (amazingly) anticipating the very fate (as sketched in the last act) of her own daughter (talking about (amazing) anticipation, is there any other similarly hair-raising case of an author (here of the text behind the libretto) so presciently staging the (exact (down to the very last details)) story of his own future tragic death) but enough digressions (sorry (this is supposed (after all) to be (although it is not the first time (and probably not the last either) it strays from the script) a technology blog))), sings

From above, we were given habit:
It is a substitute for happiness

Is this not exactly the excuse?

Reference

[1] Libretto of Onegin, in English here, in the original there.

In the circus business, the Zavatta family is a legend. From father to son and grandson, a Zavatta has for decades been the foremost clown of his generation, first in Italy, then in French North Africa, then in France proper. None was ever more famous than Achille Zavatta, who carried the family name through the sixties and seventies.

Legend or not, everyone has to make ends meet; the Zavatta troupe toured the beach resorts of Brittany in the summer, and was not above resorting to the occasional publicity gimmick to lure vacationers to the evening show.

I think I was 15, so the year must have been 1966. I was, like every year, spending the summer in Trébeurden in Northern Brittany, to which (after reading how it was forever spoiled, a decade or two later, by the unbridled development that has disgraced much of the French coast) I shall never return. Then it was paradise, if a wintry and rainy kind of paradise. We were told that at three in the afternoon a swimming competition would take place and — supreme enticement! — the winner would receive a prize of fifty francs from the very hands of Monsieur Achille Zavatta, the great clown. 50 francs was a not inconsiderable sum for a 15-year-old (with inflation it might be something like fifty dollars or euros today), but the name of the prize-giver was an even stronger attraction. So at the appointed time I was at the harbor, together with a dozen or so other boys, in our swimming suits. I don’t remember any girls; they probably had their own race.

No one has ever called me athletic. I could swim pretty well, and was good at staying in the water for a long time — I am still amazed that my parents once let me do a tour of several kilometers and several hours, far away from the coast, just by myself — but I certainly was not fast. Still, I wanted to try. At school we were always told what Pierre de Coubertin said when he founded the modern Olympic games: l’important, c’est de participer. What counts is to be in the game.

The swimming contest was a simple affair. A man on the pier told us: “See the small boat out there, where a boy is standing? You go swim around it, then you come back”. Trois, deux, un, partez: we jumped in and started moving towards the boat. I was not last, but definitely was not first; three or four boys were ahead of me, and maybe as many behind, a fair reflection of my place in the order of the world. I would never have thought of winning anyway.

Then I saw something interesting. The first swimmer, truly fast and modestly triumphant, held his hand out to the boy in the boat, who obligingly extended his own and helped him jump inside. The second followed, then the third. All were in the boat, looking quite happy with themselves.

Now I may not be the fastest swimmer in the former kingdom of Brittany, but when it comes to carrying out a clearly stated specification I do not let myself be influenced by the first guy or two, or three, who just did not pay attention. I knew what we had been told to do, and I was going to do it whatever anyone else was thinking. I went all the way to the boat, ignored the hand stretched out to me as it had been to my predecessors, swam around, and started going back towards the shore.

It did not take long for the others to realize their mistake. They jumped back. By now, however, I was far ahead. For the remainder of the race I quietly enjoyed the position of the one with whom everyone else is trying to catch up, rather than the other way around, to which I was more accustomed. They were still faster, but by then I had secured my advantage: I reached the shore first, gaining my first ever victory in a sports competition. Regrettably my last one too, so far.

In the years since, I have many times been in the company of people faster and — in science — brighter than I; often, as in the harbor of Trébeurden in the summer of 1966, they did not prevail in the end. Knowing your limitations does not mean you should let yourself be intimidated by the smart guys. How often have I seen the students whom everyone thought the most brilliant of all collapse on the day of the exam; the “most promising researcher of his generation” peter out; the author of a breakthrough paper succumb to the comfortable laziness of tenured life! Although outside of fables the race never goes to the turtle, the hare does not always win either; neither does the frog (or froggy, as I have been called a few times to my face and no doubt more behind my back); but the patient donkey, having memorized the instructions and never forgetting the destination, may well finish ahead of them all.

On that summer evening I received the fifty francs from the hands of Monsieur Achille Zavatta. In the following days I made good use of them. From the prize-giving event I remember the handshake, and the envious look of the other boys. I remember, too, my mother’s comment; at least this is the only reaction I remember from her: “Did you make sure to say ‘thank you, sir’?”.

Word

Umlottery [ˈʊm.lɑːɾɚɹi] (fr. umloterie, f; ger. Umlotterie, f.; it. umlotteria, f.; rus. умлотерия , f.).

Definition

A spur-of-the-moment and generally random decision, by a hesitant speaker of German talking in front of a (typically large) native-speaker audience, to pronounce the next intended word with, or without, an umlaut on the decisive syllable.

Example use

“My programming teacher seems to play the umlottery a lot recently, and most of the time he loses.“

Discussion

In the German language some vowels change their pronunciation under the effect of the “umlaut”, a diacritical mark appearing as a double period, as in “ä” (pronounced like an “e” in “Ted“) versus a plain “a” (pronounced “Ah“). Many nouns and verbs add umlauts in some but not all of their inflections (declinations or conjugations).  Non-native speakers find it a challenge to remember when to umlaut and when not. The consequences of incorrect umlauting can be dramatic; for example “drucken” means to print and “drücken” to press. Imagine the consequences of a police chief telling a subordinate “Print a new copy of the witness’s statement” and being understood as “Pressure the witness into making a different statement“. The stress is consequently high on the public speaker who suddenly cannot remember, in the crux of a talk, whether the first syllable of his next chosen word should be umlauted  or not.  Umlottery is the widely practiced technique of taking a big breath, silently praying to some higher power for protection, and taking a chance (as if betting at the lottery) one way or the other.

Etymology

Composite word made up from “umlaut” and “lottery”.

Origin

Precise origin unknown. First attested written occurrence in “Bertrand Meyer’s Technology Blog“, an obscure publication of dubious circulation, in October of 2012. Rumored, without independently confirmed evidence, to have been in common use in the early years of the 21st century among foreign-born professors at the ETH Zurich.

Alternative hypotheses

Some researchers have hypothesized that the word is related to the “Unified Modeling Language” (or “UML“, hence the suggestion), under the argument that using UML for a project is akin to betting on its success at the lottery. There is, however, no scholarly consensus in favor of such a connection.

A couple of weeks ago I proposed a small quiz. (I also stated that the answer would come “on Wednesday” — please understand any such promise as “whenever I find the time”. Sorry.) Here is the answer.

The quiz was:

I have a function:

• For 0 it yields 0.
• For 1 it yields 1.
• For 2 it yields 4.
• For 3 it yields 9.
• For 4 it yields 16.

What is the value for 5?

Shortly thereafter I added a hint: the value for 5 is 25, and changed the question to: “What is the value for 6?”. For good measure we can also ask about the value for 1000. Now compare your answer to  what follows.

A good answer for the value at 6 is: 34 . The function in this case is -10 + 5 x + |2 x – 3| + |2 x -7|. It matches the values for the given inputs.

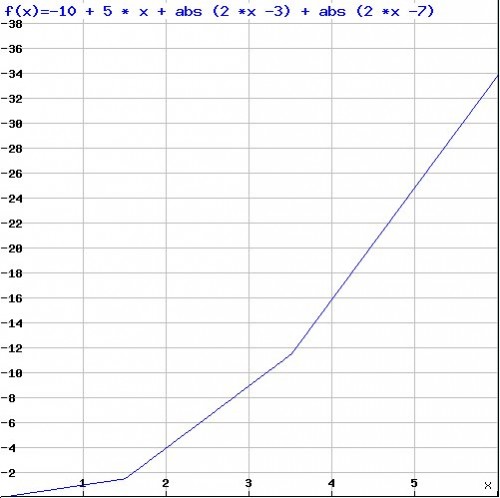
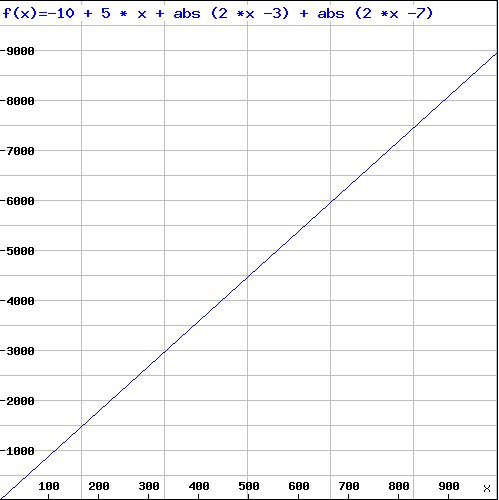
The value for 1000 is 8980:

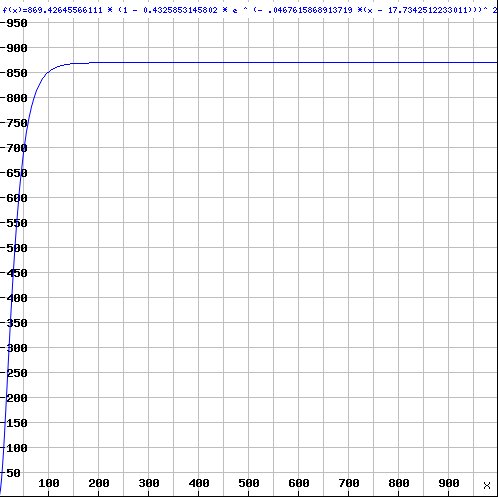
Another good answer at position 6 is 35.6. It comes up if we assume the function is over reals rather than integers; then a possible formula, which correlates very well (R-square of 0.9997) with the values at the given inputs, is:

869.42645566111 (1 – 0.4325853145802 e^{-.0467615868913719  (x – 17.7342512233011)})^{2.3116827277657443}

with a quite different asymptotic behavior, giving the value 869.4 at position 1000:

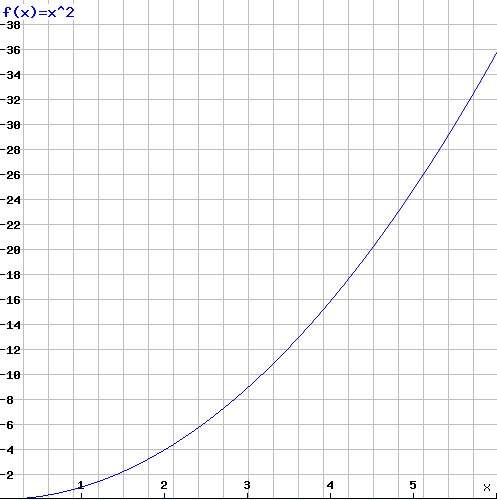
Some readers might have thought of another possibility, the square function x², which again matches all the given values:

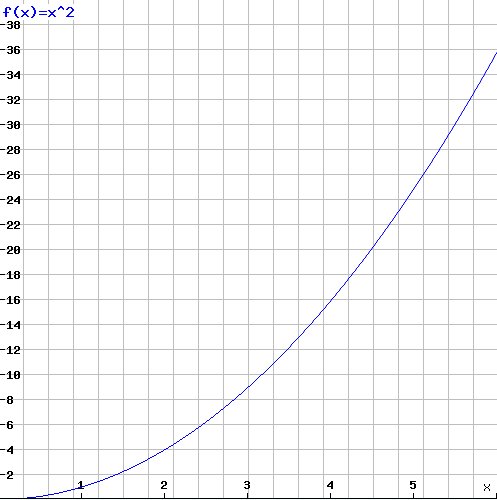
So which of these answers is right? Each is as good as the others, and as bad. There is in particular no reason to believe that the values given in the quiz’s statement suggest the square function. Any function that fits the given values, exactly (if we stick to integers) or approximately (with reals as simulated on a computer) is an equally worthy candidate. Six inputs, or six thousand, do not resolve the question. At best they are hints.

This difference between a hint and a solution is at the core of software engineering. It is, for example, the difference between a test and a specification. A test tells us that the program works for some values; as Dijkstra famously pointed out, and anyone who has developed a serious program has experienced, it does not tell us that it will work for others. The more successful tests, the more hints; but they are still only hints. I have always wondered whether Dijkstra was explicitly thinking of the Popperian notion of falsifiability: no number of experiments will prove a physical theory (although a careful experiment may boost the confidence in the theory, especially if competing theories fail to explain it, as the famous Eddington expedition did for relativity in 1919 [1]); but a single experiment can disprove a theory. Similarly, being told that our function’s value at 6 is 34 disqualifies the square function and the last one (the exponential), but does not guarantee that the first function (the linear combination) is the solution.

The specification-testing duality is the extension to computer science of the basic duality of logic. It starts with the elementary boolean operators: to prove a or b it suffices to establish a or to establish b; and to disprove a and b it suffices to show that a does not hold or to show that b does not hold. The other way round, to disprove a or b we have to show that a does not hold and to show that b does not hold; to prove that a and b holds, we have to show that a holds and to show that b holds.

Predicate calculus generalizes or to ∃, “there exists”, and and to ∀, “for all”. To prove ∃ x | p (x) (there is an x of which p holds) it suffices to find one value a such that p (a); let’s be pretentious and say we have “skolemized” x. To disprove∀ x | p (x) (p holds of all x) it suffices to find one value for which p does not hold.

In software engineering the corresponding duality is between proofs and tests, or (equivalently) specifications and use cases. A specification is like a “for all”: it tells us what must happen for all envisioned inputs. A test is like a “there exists”: it tells us what happens for a particular input and hence, as in predicate calculus, it is interesting as a disproof mechanism:

• A successful test brings little information (like learning the value for 5 when trying to figure out what a function is, or finding one true value in trying to prove a ∀ or a false value in trying to prove a ∃).
• An unsuccessful test brings us decisive information (like a false value for a ∀): the program is definitely not correct. It skolemizes incorrectness.

A proof, for its part, brings the discussion to an end when it is successful. In practice, testing may still be useful in this case, but only testing that addresses issues not covered by the proof:

• Correctness of the compiler and platform, if not themselves proved correct.
• Correctness the proof tools themselves, since most practical proofs require software support.
• Aspects not covered by the specification such as, typically, performance and usability.

But for the properties it does cover the proof is final.

It is as foolish, then, to use tests in lieu of specifications as it would be to ignore the limitations of a proof. Agile approaches have caused much confusion here; as often happens in the agile literature [2], the powerful insight is mixed up with harmful advice. The insight, which has significantly improved the practice of software development, is that the regression test suite is a key asset of a project and that tests should be run throughout. The bad advice is to ditch upfront requirements and specifications in favor of tests. The property that tests lack and specifications possess is generality. A test is an instance; a thousand tests can never be more than a thousand instances. As I pointed out in a short note in EiffelWorld (the precursor to this blog) a few years ago [3], the relationship is not symmetric: one can generate tests from a specification, but not the other way around.

The same relationship holds between use cases and requirements. It is stunning to see how many people think that use cases (scenarios) are a form of requirements. As requirements they are as useless as one or ten values are to defining a function. Use cases are a way to complement the requirements by describing the system’s behavior in selected important cases. A kind of reality check, to ensure that whatever abstract aims have been defined for the system it still covers the cases known to be of immediate interest. But to rely on use cases as requirements means that you will get a system that will satisfy the use cases — and possibly little else.

When I use systems designed in recent years, in particular Web-based systems, I often find myself in a stranglehold: I am stuck with the cases that the specifiers thought of. Maybe it’s me, but my needs tend, somehow, to fall outside of these cases. Actually it is not just me. Not long ago, I was sitting close to a small-business owner who was trying to find her way through an insurance site. Clearly the site had a planned execution path for employees, and another for administrators. Problem: she was both an employee and the administrator. I do not know how the session ended, but it was a clear case of misdesign: a system built in terms of standard scenarios. Good specification performs an extra step of abstraction (for example using object-oriented techniques and contracts, but this is for another article). Skipping this step means forsaking the principal responsibility of the requirements phase: to generalize from an analysis of the behavior in known cases to a definition of the desired behaviors in all relevant cases.

Once more, as everywhere else in computer science [4], abstraction is the key to solid results that stand the test of time. Definitely better than judging a book by its cover, inferring a function by its first few values, verifying a program by its tests, or specifying a system by its use cases.

References

[1] See e.g. a blog article: Einstein and Eddington, here.

[2] Bertrand Meyer: Agile! The Good, the Hype and the Ugly, 2013, to appear.

[3] Bertrand Meyer: Test or spec? Test and spec? Test from spec!, EiffelWorld column, 2004 available here.

[4] Jeff Kramer: Is Abstraction the Key to Computer Science?, in Communications of the ACM, vol. 50, no. 4, April 2007, pages 36-42,  available from CiteSeer here

Alexander Kogtenkov pointed out to me that precursor work to my papers on the Alias Calculus [1] [2] had been published by John Whaley and Martin Rinard [3]. There are some significant differences; in particular my rules are simpler, and their work is not explicitly presented as a calculus. But many of the basic ideas are the same. The reason I did not cite that paper is simply that I was not aware of it; I am happy to correct the omission.

References

[1] Bertrand Meyer: Towards a Theory and Calculus of Aliasing, in Journal of Object Technology, vol. 9, no. 2, March-April 2010, pages 37-74, available here (superseded by [2])
[2] Bertrand Meyer: Steps Towards a Theory and Calculus of Aliasing, in International Journal of Software and Informatics, 2011, available here (revised and improved version of [1].)
[3] John Whaley and Martin Rinard: Compositional Pointer and Escape Analysis for Java Programs, in POPL 1999, available here.

Here is a hint: the value for 5 is 25. The next question is: what is the value for 6?

For various reasons there have been no articles in recent weeks; now we are restarting on a regular basis!

A the first topic for this new season, here is a little quiz. I have a function:

• For 0 it yields 0.
• For 1 it yields 1.
• For 2 it yields 4.
• For 3 it yields 9.
• For 4 it yields 16.

The question: what is the value for 5?

Answer next Wednesday (at least it will be Wednesday in some time zone).