Bertrand Meyer's technology+ blog

Reading notes. From: Quelques éléments d’histoire des nombres négatifs (Elements of a history of negative numbers) by Anne Boyé, Proyecto Pénélope, 2002, revision available here; On Solving Equations, Negative Numbers, and Other Absurdities: Part II by Ralph Raimi, available  here; Note sur l’histoire des nombres entiers négatifs (Note on the History of Negative Numbers) by Rémi Lajugie, 2016, here;  The History of Negative Numbers by Leo Rogers, here; Historical Objections against the Number Line, by Albrecht Heeffer, here; Making Sense of Negative Numbers by Cecilia Kilhamn, 2011 PhD thesis at the University of Gothenburg, here.  Also the extensive book by Gert Schubring on Number Concepts Underlying the Development of Analysis in 17-19th Century France and Germany, here. Translations are mine (including from Maclaurin and De Morgan, retranslated from Lajugie’s and Boyé’s French citations). This excursion was spurred by a side remark in the article How to Take Advantage of the Blur Between the Finite and the Infinite by the recently deceased mathematician Pierre Cartier, available here.

At dinner recently, with non-scientists, discussion revolved about ages and a very young child, not even able to read yet, volunteered about his forthcoming little brother that “when he comes out his age will be zero”. An adult remarked “indeed, and right now his age is minus five months”, which everyone young and old seemingly found self-evident. How remarkable!

From a elite concept to grade school topic

It is a characteristic of potent advances in human understanding that for a while they are understandable to a few geniuses only, or, if not geniuses, to a handful of forward-thinking luminaries, and a generation later, sometimes less, they are taught in grade school. When I came across object-oriented programming, those of us who had seen the light, so to speak, were very few. Feeling very much like plotting Carbonari, we would excitedly meet once in a while in exotic locations (for my Simula-fueled band usually in Scandinavia, although for the Smalltalk crowd it must have been California) to share our shared passion and commiserate about the decades it would take for the rest of humankind to see the truth. Then at some point, almost overnight, without any noticeable harbinger, the whole thing exploded and from then on it was object-oriented everything. Nowadays every beginning programmer talks objects — I did not write “understands”, they do not, but that will be for another article.

Zero too was a major invention. Its first recorded use as a number (not just a marker for absent entities) was in India in the first centuries of our era. It is not hard to imagine the mockeries. “Manish here has twenty sheep, Rahul has twelve sheep, and look at that nitwit Shankar, he sold all his sheep and still claims he has some, zero of them he says! Can you believe the absurdity? Ha ha ha.”

That dialog is imaginary, but for another momentous concept, negative numbers, we have written evidence of the resistance. From the best quarters!

The greatest minds on the attack

The great Italian mathematician Cardan (Gerolamo Cardano), in his Ars Magna from 1545, was among the skeptics. As told in a 1758 French History of Mathematics by Montucla (this quote and the next few ones are from Boyé):

In his article 7 Cardan proposes an equation which in our language would be x² + 4 x = 21 and observes that the value of x can equally be +3 or -7, and that by changing the sign of the second term it becomes -3 or +7. The name he gives to such values is “fake”.

The words I am translating here as “fake values” are, in Montucla, valeurs feintes, where feint in French means feigned, or pretended (“pretend values”). Although I have not seen the text of Ars Magna, which is in Latin anyway, I like to think that Cardan was thinking of the Italian word finto. (Used for example  in the title of an opera composed by Mozart at the age of 19, La Finta Giardinera, the fake girl gardener — English has no feminine for “gardener”. The false gardenerette in question is a disguised marchioness.) It is fun to think of negative roots as feigned.

Cardan also uses terms like “abundant” versus “failing” quantities (abondantes and défaillantes in French texts) for positive and negative:

Simple advice: do not confuse failing quantities with abundant quantities. One must add the abundant quantities between themselves, also subtract failing quantities between themselves, and subtract failing quantities from abundant quantities but only by taking species into account, that is to say, only operate same with same […]

There is a recognition of negative values, but with a lot of apprehension. Something strange, the author seems to feel, is at play here. Boyé cites the precedent of Chinese accountants who could manipulate positive values through black sticks and negative ones through red sticks and notes that it resembles what Cardan seems to be thinking here. In the fifteenth century, Nicolas Chuquet “used negative numbers as exponents but referred to them as `absurd numbers’”.

For all his precautions, Cardan did consider negative quantities. No lesser mind as Descartes, a century later (La Géométrie, 1637), is more circumspect. In discussing roots of equations he writes:

Often it turns out that some of those roots are false, or less than nothing [“moindres que rien”] as if one supposes that x can also denote the lack of a quantity, for example 5, in which case we have x + 5 = 0, which, if we multiply it by x³ − 9 x²  + 26 x − 24 = 0 yields  x⁴ − 4 x³ − 19 x² + 106 x − 120 = 0, an equation for which there are four roots, as follows: three true ones, namely 2, 3, 4, and a false one, namely 5.

Note the last value: “5”. Not a -5, but a 5 dismissed as “false”. The list of exorcising adjectives continues to grow: negative values are no longer “failing”, or “fake”, or “absurd”, now for Descartes they are “false”!  To the modern mind they are neither more nor less true than the “true” ones, but to him they are still hot potatoes, to be handled with great suspicion.

Carnot cannot take the heat

One more century later we are actually taking a step back with Lazare Carnot. Not the one of the thermodynamic cycle — that would be his son, as both were remarkable mathematicians and statesmen. Lazare in 1803 cannot hide his fear of negative numbers:

If we really were to obtain a negative quantity by itself, we would have to deduct an effective quantity from zero, that is to say, remove something from nothing : an impossible operation. How then can one conceived a negative quantity by itself?.

(Une quantité négative isolée : an isolated negative quantity, meaning a negative quantity considered in isolation). How indeed! What a scary thought!

The authors of all these statements, even when they consider negative values, cannot bring themselves to talk of negative numbers, only of negative quantities. Numbers, of course, are positive: who has ever heard of a shepherd who is guarding a herd of minus 7 lambs? Negative quantities are a slightly crazy concoction to be used only reluctantly as a kind of kludge.

Lajugie mentions another example, mental arithmetic: to compute 19 x 31  in your head, it is clever to multiply (20 -1) by (30 + 1), but then as you expand the product by applying the laws of distributivity you get negative values.

De Morgan too

We move on by three decades to England and Augustus De Morgan, yes, the one who came up with the two famous laws of logic duality. De Morgan in 1803, as cited by Raimi:

8-3 is easily understood; 3 can be taken from 8 and the remainder is 5; but 3-8 is an impossibility; it requires you to take from 3 more than there is in 3, which is absurd. If such an expression as 3-8 should be the answer to a problem, it would denote either that there was some absurdity inherent in the problem itself, or in the manner of putting it into an equation.

Raimi points out that “De Morgan is not naïve” but wants to caution students about possible errors. Maybe, but we are back to fear and to words such as “absurd”, as used by Chuquet three centuries before. De Morgan (cited by Boyé) doubles down in his reluctance to accept negatives as numbers:

0 − a is just as inconceivable as -a.

Here is an example. A father is 56 years old and his [son] is 29 years old. In how many years will the father’s age be twice his son’s age? Let x be that number of years; x satisfies 56 +x = 2 (29 + x). We find x = -2.

Great, we say, he got it! This simple result is screaming at De Morgan but he has to reject it:

This result is absurd. However if we change x into -x and correspondingly resolve 56−x = 2 (29−x), we find x = -2. The [previous] negative answer shows that we had made an error in the initial phrasing of the equation.

In other words, if you do not like the solution, change the problem! I too can remember a few exam situations in which I would have loved to make an equation more sympathetic by replacing a plus sign with a minus. Too bad no one told me I could.

De Morgan’s comment is remarkable as the “phrasing of  the equation” contained no “error” whatsoever.   The equation correctly reflected the problem as posed. One could find the statement of the problem mischievous (“in how many years” suggests a solution in the future whereas there is only one in the past), but the equation is meaningful and  has a solution — one, however, that horrifies De Morgan. As a result, when discussing the quadratic (second-degree) equation ax² + bx + c = 0, instead of accepting that a, b and c can be negative, he distinguishes no fewer than 6 cases, such as ax² – bx + c = 0, ax² + bx – c = 0 etc. The coefficients are always non-negative, it is the operators that change between + and  -. As a consequence, the determinant actually has two possible values, the one familiar to us, b² – 4ac, but also b² + 4ac for some of the cases. According to Raimi, many American textbooks of the 19th century taught that approach, forcing students to remember all six cases. (For a report about a current teaching distortion of the same topic, see a recent article on the present blog, “Mathematics Is Not a Game of Hit and Miss”, here.)

De Morgan (cited here by Boyé) feels the need to turn this reluctance to use negative numbers into a general rule:

When the answer to a problem is negative, by changing the sign of x in the equation that produced the result, we can discover that an error was made in the method that served to form this equation, or show that the question asked by the problem is too limited.

Sure! It is no longer “if the facts do not fit the theory, change the facts” (a sarcastic definition of bad science), but also “if you do not like the solution, change the problem”. All the more unnecessary (to a modern reader, who thanks to the work of countless mathematicians over centuries learned negative numbers in grade school, and does not spend time wondering whether they mean something) that if we keep the original problem the computed solution, x = -2, makes perfect sense: the father was twice his son’s age two years ago. The past is a negative future. But to see things this way, and to accept that there is nothing fishy here, requires a mindset for which an early 19-th century mathematician was obviously not ready.

And Pascal, and Maclaurin

Not just a mathematician but a great mathematical innovator. What is remarkable in all such statements against negative numbers is that they do not emanate from little minds, unable to grasp abstractions. Quite the contrary! These negative-number-skeptics are outstanding mathematicians. Lajugie gives more examples from the very top. Blaise Pascal in 1670:

Too much truth surprises; I know people who cannot understand that when you deduct 4 from zero, what remains is zero.

(Oh yes?, one is tempted to tell the originator of probability theory, who was fascinated by betting and games of chance: then I put the 4 back and get 4? Quick way to get rich. Give me the address of that casino please.) A friend of Pascal, skeptical about the equality -1 / 1 = 1 / -1: “How could a smaller number be to a larger one as a larger one to a smaller one?”. An English contemporary, John Wallis, one of the creators of infinitesimal calculus — again, not a nitwit! — complains that a / 0 is infinity, but since in a / -1 the denominator is lesser than zero it must follow that a / -1, which is less than zero (since it is negative by the rule of signs), must also be greater than infinity! Nice one actually.

This apparent paradox also bothered the great scientist D’Alembert, the 18-th century co-editor of the Encyclopédie, who resolves it, so to speak, by stating (as cited by Heeffer) that “One can only go from positive to negative through either zero or through infinity”; so unlike Wallis he accepts that 1 / -a is negative, but only because it becomes negative when it passes through infinity. D’Alembert concludes (I am again going after Heeffer) that it is wrong to say that negative numbers are always smaller than zero. Euler was similarly bothered and similarly looking for explanations through infinity: what does Leibniz’s expansion of 1 / (1 – x)  into 1 + x + x² + x³ + … become for x = 2? Well, the sum 1 + 2 + 4 + 8 + … diverges, so 1 / -1 is infinity!

We all know the name “Maclaurin” from the eponymous series. Colin Maclaurin  wrote in 1742, decades after Pascal (Boyé):

The use of the negative sign in algebra leads to several consequences that one initially has trouble accepting and has led to ideas that seem not to have any real foundation.

Again the supposed trouble is the absence of an immediately visible connection to everyday reality (a “real foundation”). And again Maclaurin accepts that quantities can be negative, but numbers cannot:

While abstract quantities can be both negative and positive, concrete quantities are not always capable of being the opposite of each other.

(cited by Kilhamn). Apparently Colin’s wife Anne never thought of buying him a Réaumur thermometer (see below) for his birthday.

Yes, two negatives make a positive

We may note that the authors cited above, and many of their contemporaries, had no issue manipulating negative quantities in some contexts, and to accept the law of signs, brilliantly expressed by the Indian mathematician Brahmagupta  in the early 7th century (not a typo); as cited by Rogers:

A debt minus zero is a debt.

A fortune minus zero is a fortune.

Zero minus zero is a zero.

A debt subtracted from zero is a fortune.

A fortune subtracted from zero is a debt.

The product of zero multiplied by a debt or fortune is zero.

The product of zero multiplied by zero is zero.

The product or quotient of two fortunes is one fortune.

The product or quotient of two debts is one fortune.

The product or quotient of a debt and a fortune is a debt.

The product or quotient of a fortune and a debt is a debt.

That view must have been clear to accountants. Whatever Pascal may have thought, 4 francs removed from nothing do not vanish; they become a debt. What the great mathematicians cited above could not fathom was that there is such a thing as a negative number. You can count up as far as your patience will let you; you can then count down, but you will inevitably stop. Everyone knows that, and even Pascal or Euler have trouble going beyond. (Old mathematical joke: “Do you know about the mathematician who was afraid of negative numbers? He will stop at nothing to avoid them”.)

The conceptual jump that took centuries to achieve was to accept that there are not only negative quantities, but negative numbers: numbers in their own right, not just temporarily  negated positive numbers (that is, the only ones to which we commonly rely in everyday life), prefaced with a minus sign because we want to use them as “debts”, but with the firm intention to move them back to the other side so as to restore their positivity  — their supposed naturalness —  at the end of the computation. We have seen superior minds “stopping at nothing” to avoid that step.

Others were bolder; Schubring has a long presentation of how Fontenelle, an 18-th century French scientist and philosopher who contributed to many fields of knowledge,  made the leap.

Not everyone may yet get it

While I implied above that today even small children understand the concept, we may note in passing that there may still be people for whom it remains a challenge. Lajugie notes that the Fahrenheit temperature scale frees people from having to think about negative temperatures in ordinary circumstances, but since the 18-th century the (much more reasonable) Réaumur thermometer and Celsius scale goes under as well as above zero, helping people get familiar with negative values as something quite normal and not scary. (Will the US ever switch?)

Maybe the battle is not entirely won.  Thanks to Rogers I learned about the 2018 Lottery Incident in the United Kingdom of Great Britain and Northern Ireland, where players could win by scratching away, on a card, a temperature lower than the displayed figure. Some temperatures were below freezing. The game had to be pulled after less than a week as a result of player confusion. Example complaints included this one from a  23-year-old who was adamant she should have won:

“On one of my cards it said I had to find temperatures lower than -8. The numbers I uncovered were -6 and -7 so I thought I had won, and so did the woman in the shop. But when she scanned the card the machine said I hadn’t. I phoned Camelot [the lottery office] and they fobbed me off with some story that -6 is higher – not lower – than -8 but I’m not having it. I think Camelot are giving people the wrong impression – the card doesn’t say to look for a colder or warmer temperature, it says to look for a higher or lower number. Six is a lower number than 8. Imagine how many people have been misled.“

Again, quantities versus numbers. As we have seen, she could claim solid precedent for this reasoning. Most people, of course, have figured out that while 8 is greater than 6 (actually, because of that), -6 is greater than -8. But as Lajugie points out the modern, rigorous definition of negative numbers is (in the standard approach) far from the physical intuition (which typically looks like the two-directional line pictured at the beginning of this article, with numbers spreading away from zero towards both the right and the left). The picture helps, but it is only a picture.

Away from the perceptible world

If we ignore the intuition coming from observing a Réaumur or Celsius thermometer (which does provide a “real world” guide), the early deniers of negative numbers were right that this concept does not directly reflect the experiential understanding of numbers, readily accessible to everyone. The general progress of science, however, has involved moving away from such immediate intuition. Everyday adventures (such as falling on the floor) absolutely do not suggest to us that matter is made of sparse atoms interacting through electrical and magnetic phenomena. This march towards abstraction has guided the evolution of modern science — most strikingly, the evolution of modern mathematics.

Some lament this trend; think of the negative reactions to the so-called “new math”. (Not from me. I was caught by the  breaking of the wave and loved every minute of it.) But there is no going back; in addition, it is well known that some of the initially most abstract mathematical development, initially pursued without any perceived connection with reality, found momentous unexpected applications later on; two famous examples are Minkowski’s space-time formalism, which provided the mathematical framework for specifying relativity, and number-theoretical research about factoring large numbers into primes, which made modern cryptography (and hence e-commerce) possible.

Negative numbers too required abstraction to acquire mathematical activity. That step required setting aside the appeal to intuition and considering the purely concepts solely through its posited properties. We computer scientists would say “applying the abstract data type approach”. The switch took place sometime in the middle of the 19th century, spurred among others by Évariste Galois. The German mathematician Hermann Hankel — who lived only a little longer than Galois — explained clearly how this transition occurred for negative numbers (cited by Boyé among others):

The [concept of] number is no longer today a thing, a substance that is supposed to exist outside of the thinking subject or the objects that lead to it being considered; it is no longer an independent principle, as the Pythagoreans thought. […] The mathematician considers as impossible only that which is logically impossible, in the sense of implying a contradiction. […] But if the numbers under study are logically possible, if the underlying concept is defined clearly and distinctly, the question can no longer be whether a substrate exists in the world of reality.

A very modern view: if you can dream it, and you can make it free of contradiction (well, Hankel lived in the blissful times before Gödel), then you can consider it exists. An engineer might replace the second of these conditions by: if you can build it. And a software engineer, by: if you can compile and run it. In the end it is all the same idea.

Formally: a general integer is an equivalence class

In modern mathematics, while no one forbids you from clinging for help to some concrete intuition such as the Celsius scale, it is not part of the definition. Negative numbers are formally defined members of the zoo.

For those interested (and not remembering the details), the rigorous definition goes like this. We start from zero-or-positive integers (the set N of “natural” numbers) and consider pairs [a, b] of numbers (as we would do to define rationals, but the sequel quickly diverges). We define an equivalence relation which holds with another pair [a’, b’] if a + b’ = a’ + b. Then we can define the set Z of all integers (positive, zero, negative) as the quotient of N x N by that relation. The intuition if that the characteristic property of an equivalence class, such as [1, 4], [2, 5],  [3, 6]… , is that b – a, the difference between the second and first values, is the same for all pairs: 3 in this example (4 – 1, 5 – 2, 6 – 3 etc.). At least that property holds for b >= a; since we are starting from N, subtraction is defined only in that case. But then if we take that quotient as the definition of Z, we call members of that set “negative”, by pure convention, whenever b < a (if this property holds for one of the pairs in an equivalence class it holds for all of them), and positive if b > a. Zero is obtained for a = b.

We reestablish the connection with our good old natural integers by identifying N with the subset of Z for which b >= a. (This is an informal statement; the correct technical phrasing is that there is a “bijection” — a one-to-one correspondence, in fact an isomorphism — between that subset and N.) So we have plunged, or “embedded”, N into something bigger, to which most of its treasured properties (associativity and commutativity of addition etc.) immediately spread, while some limitations disappear; in particular, unlike in N, we can now subtract any Z integer from any other.

We also get the opposites of numbers as a result: for any m in Z, we can easily prove that there is another one n such that m + n = 0. That n can be written -m. The property is true for both positive and negative numbers, concepts that are also easy to define: we show that “>” is one of those operations that extend from N to Z, and the positive numbers are those m such that m > 0. Then if m is positive -m is negative, and conversely; 0 is the only number for which m = -m.

Remarkably, Z too is in one-to-one correspondence with N. (It is one of the definitions of an infinite set that it can be in one-to-one correspondence with one of its strict subsets, something that is obviously not possible for a finite set. To shine in cocktail parties you can refer to this property as “Dedekind-infinite”.) In other words, we have uncovered yet a new attraction of Hilbert’s Grand Hotel: the hotel has an annex, ready for the case of a guest coming with an unannounced companion. The companion will be hosted in the annex, in a room uniquely paired with the original guest’s room. The annex is a second hotel, but it is not exactly like the first: it does not have an annex of its own in the form of yet another hotel. It does have an annex, but that is the original hotel (the hotel of which it itself is the annex).

If you were not aware of the construction through equivalence classes of pairs and your reaction is “so much ado about so little! I do not need any of this to understand negative numbers and to know that m + -m = 0”, well, maybe, but you are missing part of the story: the observation that even the “natural” numbers are not that natural. Those we can readily apprehend as part of “natural” reality are the ones from 1 to something like 1000,  denoting quantities that we can reasonably count. If you really have extraordinary patience and time make this 1000,000 or even 1 million, that does not change the argument.

Even zero, as noted, took millennia to be recognized as a number. Beyond the numbers that we can readily fathom in relation to our experience at human scale, the set of natural integers is also an intellectual fiction. (Its official construction in the modern mathematical canon is seemingly even more contorted than the extension to Z sketched above: N, in the so-called Zermelo-Fraenkel theory (more pickup lines for cocktail parties!) contains the empty set for 0, and then sets each containing the previous one and a set made of that previous one. It is clearer with symbols: ø, {ø}, {ø, {ø}}, {ø, {ø}, {ø, {ø}}}, ….)

Coming back to negative numbers, Riemann (1861, cited by Schubring) held their construction as a fundamental step in the generalization process that characterizes mathematics, beautifully explaining the process:

The original object of mathematics is the integer number; the field of study increases only gradually. This extension does not happen arbitrarily, however; it is always motivated by the fact that the initially restricted view leads toward a need for such an extension. Thus the task of subtraction requires us to seek such quantities, or to extend our concept of quantity in such a way that its execution is always possible, thus guiding us to the concept of the negative.

Nature and nurture

The generalization process is also a process of abstraction. The move away from the “natural” and “intuitive” is inevitable to understand negative numbers. All the misunderstandings and fears by great minds, reviewed above, were precisely caused by an exaggerated, desperate attempt to cling to supposedly natural concepts. And we only talked about negative numbers! Similar or worse resistance met the introduction of imaginary and complex numbers (the names themselves reflect the trepidation!), quaternions and other fruitful but artificial creation of mathematics. Millenia before, the Greeks experienced shock when they realized that numbers such as π and the square root of 2 could not be expressed as ratios of integers.

Innovation occurs when someone sets out to disprove a statement of impossibility. (This technique also lies behind one approach to solving puzzles and riddles: you despair that there is no way out; then try to prove that there is no solution. Failing to complete that proof might end up opening for you the path to one.)

Parallels exist between innovators and children. Children do not know yet that some things are impossible; they make up ways. Right now I am sitting next to the Rhine and I would gladly take a short walk on the other bank, but I do not want to go all the way to the bridge and back. If I were 4 years old, I would dream up some magic carpet or other fancy device, inferred from bedtime stories, that would instantly transport me there. We grow up and learn that there are no magic carpets, but true innovators who see an unsolved problem refuse to accept that state of affairs.

In their games, children often use the conditional: “I would be a princess, and you would be a magician!”. Innovators do this too when they refuse to be stopped by conventional-wisdom statements of impossibility. They set out to disprove the statements. The French expression “prouver le mouvement en marchant”, prove movement by walking, refers to the Greek philosophers Diogenes of Sinope and  Zeno of Elea. Zeno, the story goes, used the paradox of Achilles and the tortoise to claim he had proved that movement is impossible. Diogenes proved the reverse by starting to walk.

In mathematics and in computer science, we are even more like children because we can in fact summon our magic carpets — build anything we dream of, provided we can define it properly. Mathematics and computer science are among the best illustrations of Yuval Noah Harari’s thesis that a defining characteristic of the human race is our ability to tell ourselves stories, including very large and complex stories. A mathematical theory is a story that we tell ourselves and to which we can convert other mathematicians (plus, if the theory is really successful, generations of future students). Computer programs are the same with the somewhat lateral extra condition that we must also enable some computing system to execute it, although that system is itself a powerful story that has undergone the same process. You can find variants of these observations in such famous pronouncements as Butler Lampson’s “in computer science, we can solve any problem by introducing an extra level of indirection” and Alan Kay‘s  “the best way to predict the future is to invent it”.

There is a difference, however, with children’s role-playing; and it can have dramatic effects. Children can indulge in make-believe for quite some time, continuing to live their illusions until they grow up and become reasonable. Normally they will not experience bad consequences (well, apart from the child who believes a little too hard, or from a window little too high, that his arms really are wings.) In adult innovation, sooner or later you have to reconcile the products of your imagination with the world. It may be the physical world (your autonomous robot was fantastic in the lab but it requires heavy batteries making it impractical), but things are just as bad with the virtual world of mathematics or software. It is great to define and extend your own freaky artificial worlds, but at some point you have to make sure they are consistent not just with already defined worlds but with themselves. As noted earlier, a mathematical concoction, however audacious, should be free of contradictions; and a software concept, however powerful, should be implementable. (Efficiently implementable.)

By any measure the most breathtaking virtual construction of modern mathematics is Cantor’s set theory, which scared many mathematicians,  the way negative numbers had terrified their predecessors. (Case in point: the editor of a journal to which Cantor had submitted a paper wrote that it was “a hundred years too soon”.  Cantor did not want to wait until 1984. The great mathematician Kronecker described him as “a corrupter of youth”. And so on.) More enlightened colleagues, however, soon recognized the work as ushering in a new era. Hilbert, in particular, was a great supporter, as were many of the top names in several countries. Then intellectual disaster struck.

Cantor himself and others, most famously Russell in a remark included in a letter of Frege, noticed a problem. If sets can contain other sets, and even contain themselves (the set of infinite sets must be infinite), what do we make of the set of all sets that do not contain themselves? Variants of this simple question so shook the mathematical edifice that it took a half-century to put things back in order.

Dream, check, build

Cantor, for his part, went into depression and illness. He died destitute and desperate. There may not have been a direct cause-to-effect relationship, but certainly the intellectual rejection and crisis did not help.

All the sadder that in the end set theory, after significant cleanup, turned out to be one of the biggest successes of history. We still discuss the paradoxes, but it is unlikely that today they prevent anyone from sleeping soundly at night.

Unlike those genuinely disturbing paradoxes of set theory, the paradoxes that led mathematicians of previous centuries to reject negative numbers were apparent only. They were not paradoxes but tokens of intellectual timidity.

The sole reason for fearing and skirting negative numbers was an inability to accept a construction that contradicted a simplistic view of physical reality. Like object-oriented programming and many other bold advances, all that was required was the audacity to take imagined abstractions seriously.

Dream it; check it; build it.

I was recently looking at the math exercises of a 14-year-old, having to do with quadratic (second-degree) equations.

The first thing that caught my eye is not a surprise: the difference between school and life. The quadratic polynomials appearing in the exercises, such as x² – x – 6, all happen to have integer roots (3 and -2 in this case). Also, they all have 1 as the second-degree coefficient (the `a’ in a x² + b x + c). There are good pedagogical reasons for these choices: with more general parameters, solving the equation becomes a task of numerical computation, which has no connection to the topic. But in any real-life application (say, the computation of where a ball thrown into the air will hit the ground) the solution will not come ready-made as in these school exercises.

I found one of the exercises very good. It reads this way (this is a Zurich school, I am translating from the German): A pencil factory has two machines. To produce 100 pencils, the older machine would take 10 minutes more than both machines running together. If in a minute the newer machine produces 32 pencils, how many does the older one produce in the same time? It provides a good opportunity to practice how to model a problem by defining the appropriate mathematical parameters. Then  — surprise  — you get a quadratic equation whose  solutions  — surprise  — are integers (only one of which makes sense). Useful gymnastics.

Another interesting example is the  equation

Interesting because if you do not use a bit of insight you will not get anywhere; after all, there is a range of 4 for the exponents (from -1 for the square root  to  0 for the constants, 1 for the terms in x, and 2 for the terms in x²), so squaring both sides to get rid of the square root, for example, would be hopeless. Now if you remember that this exercise goes with a lecture about 2_^nd-degree equations and apply what you have learned about them, you get the roots of the polynomial in the denominator on the left, x² – x – 6, and can rewrite it as (x – 3) (x + 2). Then you notice that x – 3 also appears, multiplied by 5, in the right-side denominator; so you remove it on both sides, and from then it is all downhill: you get another quadratic equation which  — surprise  — has simple roots.

Throughout these exercises I see, introduced from the start, an idea that not all people having learned quadratic equations remember: the rule that any second-degree polynomial a x² + b x + c can be written a (x – x₀) (x – x₁) where x₀ and  x₁ are the roots (including when they are the same). It is often useful to turn such a polynomial into this form (particularly simple when a = 1).

Then I probed  further and asked the student what he would do if the roots were not such simple integers. It turns out that he had no idea since that is not something they are taught at that level! They have not heard about the notion of determinant (b² – 4 a c), and how it gives the solutions, through the standard formula: (-b ± d) / 2 a where d is the square root of the determinant.

I realized that the way they are taught to “solve” the equation (I have to put the word in quotes) is to try to guess some integer values that will make x² + b x + c (good thing that a = 1 for all the examples!) zero. Specifically, you try out values u and v whose product is c and check whether (x – u) (x – v) works out to the given polynomial. If not, you continue guessing values until you find a pair that works. Mathematics as a game of hit-and-miss.

In the x² – x – 6 example, let’s see… -3 and +2? Oh no, they do not fit. 1 and -6? Bummer. 6 and -1?  Also not. Maybe -2 and +3? Bingo!

This method of poking around until you find something that clicks seems to me a strange thing to teach. I should include a caveat here: I am not an expert in mathematical pedagogy (and not even a mathematician). So I am asking questions, not passing judgment. Also, the place being Switzerland, where processes are usually thought out carefully, especially in education, I have to assume that whoever designed this curriculum had some hunch of what he was doing. But the result is puzzling. The kind of mathematics that helps people (and on which today’s world rests, whether directly or through physics and computer science) is not about guessing results. It is about establishing rules, in the form of axioms and theorems, proving the latter (from the former), and then relying on them to derive whatever specific results you need. The edifice of rules has a deep and elaborate structure, devised over centuries by giants standing on the shoulders of giants standing on the shoulders of other giants. But once you have a rule you no longer have to go to the underlying layers; you directly use the result of the combined work of countless smart people. It does not matter how many times they tried to derive them and how many mistakes they made along the way: their work has been vetted many times, and you can use its outcome in full confidence.

If I use my guessing powers to try values that might make a x² + b x + c zero, I will succeed once in a while, particularly for schoolbook exercises. When I do not succeed, I have no clue whether the reason is my insufficient intellectual agility, the absence of simple solutions (integers or simple fractions), or the absence of any solution (students at the level under consideration have not heard of imaginary numbers yet). If I learn the formula  (meaning, with a good teacher, not only learning it as a recipe but discovering why the recipe works), I am equipped to solve any quadratic equation, with or without  simple integer solutions. When solving such equations I do not need to apply ingenuity to guess solutions, a remarkably pointless exercise (except maybe the first few times). I can reserve my ingenuity to more interesting pursuits.

Indeed there would be so much more to teach. I looked at the textbook with its many pages of examples of quadratic equation to solve; more accurately, to guess. All piecemeal, example by example; no attempt at generality (isn’t the quest for general results one of the prime characteristics of the mathematical spirit?) They are not even taught that sometimes there are no solutions among the numbers they know; good luck to the enterprising student who, having found the roots of x² – x – 6 through the recommended approach of trial and error, confidently embarks on solving x² – x + 6 = 0 (it is almost the same and so cannot be much harder, right?).

All that space and student attention are wasted at the expense of the theoretical and practical properties of quadratic equations, second-degree polynomials and parabolas. We could direct students to web sites such as this one where they can play with parabolas, try different parameters and animate the results. We could explain how quadratic equations serve as a fundamental tool for computing trajectories of projectiles. We could even introduce the notion of parabolic mirror and its very practical benefit following from a basic geometrical property. And we could put all this into a form that a 14-year-old will readily understand.

Mathematics is not just about applications. I also feel sorry that these children, by just being shown haphazard tricks, miss the sheer beauty of the underlying ideas, which struck many of us when we learned them at the same age. What a pity.

There may be a grand plan behind the way these topics get taught, but I do not see it. I only see an approach that seems poised to drill into young minds the conviction that mathematics is but a sad, boring and pointless game of tricks.

Thanks to Manuel Oriol for useful observati9ns.

On 13-15 September 1999 a symposium took place in St Catherine College in Oxford,  in honor of Tony Hoare’s “retirement” from Oxford (the word is in quotes because he has had several further productive careers since). The organizers were Jim Woodcock, Bill Roscoe and Jim Davies. The proceedings are available as Millenial Perspectives in Computer Science, MacMillan Education UK, edited by Davies, Roscoe and Woodcock. The Symposium was a milestone event.

As part of a recent conversation on something else, YuQian Zhou(who was also there) sent me a group photo from the event, which I did not know even existed. I am including it below; it is actually a photo of a paper photo but the resolution is good. It is a fascinating gallery of outstanding people in programming and verification. (How many Turing award winners can you spot? I see 7.)

Many thanks to YuQian Zhou, Jim Woodcock and Bill Roscoe for insights into the picture in discussions of the past two weeks.

Maria Naumcheva, Sophie Ebersold, Alexandr Naumchev, Jean-Michel Bruel, Florian Galinier and Bertrand Meyer: Object-Oriented Requirements: a Unified Framework for Specifications, Scenarios and Tests, in JOT (Journal of Object Technology), vol. 22, no. 1, pages 1:1-19, 2023. Available here with link to PDF  (the journal is open-access).

From the abstract:

A paradox of requirements specifications as dominantly practiced in the industry is that they often claim to be object-oriented (OO) but largely rely on procedural (non-OO) techniques. Use cases and user stories describe functional flows, not object types.

To gain the benefits provided by object technology (such as extendibility, reusability, and reliability), requirements should instead take advantage of the same data abstraction concepts – classes, inheritance, information hiding – as OO design and OO programs.

Many people find use cases and user stories appealing because of the simplicity and practicality of the concepts. Can we reconcile requirements with object-oriented principles and get the best of both worlds?

This article proposes a unified framework. It shows that the concept of class is general enough to describe not only “object” in a narrow sense but also scenarios such as use cases and user stories and other important artifacts such as test cases and oracles. Having a single framework opens the way to requirements that enjoy the benefits of both approaches: like use cases and user stories, they reflect the practical views of stakeholders; like object-oriented requirements, they lend themselves to evolution and reuse.

The article builds in part on material from chapter 7 of my requirements book (Handbook of Requirements and Business Analysis, Springer).

I am happy to announce the publication of the Handbook of Requirements and Business Analysis (Springer, 2022).

It is the result of many years of thinking about requirements and how to do them right, taking advantage of modern principles of software engineering. While programming, languages, design techniques, process models and other software engineering disciplines have progressed considerably, requirements engineering remains the sick cousin. With this book I am trying to help close the gap.

The Handbook introduces a comprehensive view of requirements including four elements or PEGS: Project, Environment, Goals and System. One of its principal contributions is the definition of a standard plan for requirements documents, consisting of the four corresponding books and replacing the obsolete IEEE 1998 structure.

The text covers both classical requirements techniques and novel topics such as object-oriented requirements and the use of formal methods.

The successive chapters address: fundamental concepts and definitions; requirements principles; the Standard Plan for requirements; how to write good requirements; how to gather requirements; scenario techniques (use cases, user stories); object-oriented requirements; how to take advantage of formal methods; abstract data types; and the place of requirements in the software lifecycle.

The Handbook is suitable both as a practical guide for industry and as a textbook, with over 50 exercises and supplementary material available from the book’s site.

You can find here a book page with the preface and sample chapters.

To purchase the book, see the book page at Springer and the book page at Amazon US.

Short version: the full text of my Introduction to the Theory of Programming Languages book (second printing, 1991) is now available. This page has more details including the table of chapters, and a link to the PDF (3.3MB, 448 + xvi pages).

The book is a survey of methods for language description, particularly semantics (operational, translational, denotational, axiomatic, complementary) and also serves as an introduction to formal methods. Obviously it would be written differently today but it may still have its use.

A few days ago I released the Axiomatic Semantics chapter of the book, and the chapter introducing mathematical notations. It looked at the time that I could not easily  release the rest in a clean form, because it is impossible or very hard to use the original text-processing tools (troff and such). I could do it for these two chapters because I had converted them years ago for my software verification classes at ETH.

By perusing old files, however,  I realized that around the same time (early 2000s) I actually been able to produce PDF versions of the other chapters as well, even integrating corrections to errata  reported after publication. (How I managed to do it then I have no idea, but the result looks identical, save the corrections, to the printed version.)

The figures were missing from that reconstructed version (I think they had been produced with Brian Kernighan’s PIC graphical description language , which is even more forgotten today than troff), but I scanned them from a printed copy and reinserted them into the PDFs.

Some elements were missing from my earlier resurrection: front matter, preface, bibliography, index. I was able to reconstruct them from the original troff source using plain MS Word. The downside is that they are not hyperlinked; the index has the page numbers (which may be off by 1 or 2 in some cases because of reformatting) but not hyperlinks to the corresponding occurrences as we would expect for a new book. Also, I was not able to reconstruct the table of contents; there is only a chapter-level table of contents which, however, is hyperlinked (in other words, chapter titles link to the actual chapters). In the meantime I obtained the permission of the original publisher (Prentice Hall, now Pearson Education Inc.).

Here again is the page with the book’s description and the link to the PDF:

bertrandmeyer.com/ITPL

The latest issue of the New York Review of Books contains a book review by George Stauffer about Alban Berg with this bewildering sentence about Berg’s childhood:

He showed few signs of musical talent as a youth aside from informal piano lessons, reading through the scores of songs and operas, and playing four-hand arrangements of orchestral and chamber works with his sister, Smaragda.

Well, well… “Aside from”? If you had a child who could only read through lots of opera scores and play four-hand arrangements of symphonies, would you immediately get to the logical conclusion that he is devoid of musical talent?

(Sorry about poor Alban, he is the shame of our family, let’s just hope Smaragda won’t turn out to be such an abject musical failure.)

There is a new paper out, several years in the making:

The Role of Formalism in System Requirements
Jean-Michel Bruel, Sophie Ebersold, Florian Galinier, Manuel Mazzara, Alexander Naumchev, Bertrand Meyer
Computing Surveys (ACM), vol. 54, no. 5, June 2021, pages 1-36
DOI: https://doi.org/10.1145/3448975
Preprint available here.

The authors are from the Schaffhausen Institute of Technology in Switzerland, the University of Toulouse in France and Innopolis University in Russia. We make up a cross-institutional (and unofficial) research group which has for several years now been working on improving the state of software requirements, with both an engineering perspective and an interest in taking advantage of formal methods.

The article follows this combined formal-informal approach by reviewing the principal formal methods in requirements but also taking into consideration non-formal ones — including techniques widely used in industry, such as DOORS — and studying how they can be used in a more systematic way. It uses a significant example (a “Landing Gear System” or LGS for aircraft) to compare them and includes extensive tables comparing the approaches along a number of systematic criteria.

Here is the abstract:

A major determinant of the quality of software systems is the quality of their requirements, which should be both understandable and precise. Most requirements are written in natural language, which is good for understandability but lacks precision.

To make requirements precise, researchers have for years advocated the use of mathematics-based notations and methods, known as “formal.” Many exist, differing in their style, scope, and applicability.

The present survey discusses some of the main formal approaches and compares them to informal methods.The analysis uses a set of nine complementary criteria, such as level of abstraction, tool availability, and traceability support. It classifies the approaches into five categories based on their principal style for specifying requirements: natural-language, semi-formal, automata/graphs, mathematical, and seamless (programming-language-based). It includes examples from all of these categories, altogether 21 different approaches, including for example SysML, Relax, Eiffel, Event-B, and Alloy.

The review discusses a number of open questions, including seamlessness, the role of tools and education, and how to make industrial applications benefit more from the contributions of formal approaches.

For me, of course, this work is the continuation of a long-running interest in requirements and specifications and how to express them using the tools of mathematics, starting with a 1985 paper, still being cited today, with a strikingly similar title: On Formalism in Specifications.

Trivia: the “response to referees” (there were no fewer than eight of them!) after the first review took up 85 pages. Maybe not for the Guinness Book, but definitely a personal record. (And an opportunity to thank the referees for detailed comments that considerably helped shape the final form of the paper.)

Correction (20 July 2021): I just noted that I had forgotten to list myself among the authors! Not a sign of modesty (I don’t have any), more of absent-mindedness. Now corrected.

Science progresses through people taking advantage of others’ insights and inventions. One of the conditions that makes the game possible is that you acknowledge what you take. For the originator, it is rewarding to see one’s ideas reused, but frustrating when that happens without acknowledgment, especially when you are yourself punctilious about citing your own sources of inspiration.

I have started to record some concepts that are widely known and applied today and which I believe I originated in whole or in part, whether or not their origin is cited by those who took them. The list below is not complete and I may update it in the future. It is not a list of ideas I contributed, only of those fulfilling two criteria:

• Others have built upon them.  (If there is an idea that I think is great but no one paid attention to it, the list does not include it.)
• They have gained wide visibility.

There is a narcissistic aspect to this exercise and if people want to dismiss it as just showing I am full of myself so be it. I am just a little tired of being given papers to referee that state that genericity was invented by Java, that no one ever thought of refactoring before agile methods, and so on. It is finally time to state some facts.

Facts indeed: I back every assertion by precise references. So if I am wrong — i.e. someone preceded me — the claims of precedence can be refuted; if so I will update or remove them. All articles by me cited in this note are available (as downloadable PDFs) on my publication page. (The page is up to date until 2018; I am in the process of adding newer publications.)

Post-publication note: I have started to receive some comments and added them in a Notes section at the end; references to those notes are in the format [A].

Final disclaimer (about the narcissistic aspect): the exercise of collecting such of that information was new for me, as I do not usually spend time reflecting on the past. I am much more interested in the future and definitely hope that my next contributions will eclipse any of the ones listed below.

Programming concepts: substitution principle

Far from me any wish to under-represent the seminal contributions of Barbara Liskov, particularly her invention of the concept of abstract data type on which so much relies. As far as I can tell, however, what has come to be known as the “Liskov Substitution Principle” is essentially contained in the discussion of polymorphism in section 10.1 of in the first edition (Prentice Hall, 1988) of my book Object-Oriented Software Construction (hereafter OOSC1); for example, “the type compatibility rule implies that the dynamic type is always a descendant of the static type” (10.1.7) and “if B inherits from A, the set of objects that can be associated at run time with an entity [generalization of variable] includes instances of B and its descendants”.

Perhaps most tellingly, a key aspect of the substitution principle, as listed for example in the Wikipedia entry, is the rule on assertions: in a proper descendant, keep the invariant, keep or weaken the precondition, keep or strengthen the postcondition. This rule was introduced in OOSC1, over several pages in section 11.1. There is also an extensive discussion in the article Eiffel: Applying the Principles of Object-Oriented Design published in the Journal of Systems and Software, May 1986.

The original 1988 Liskov article cited (for example) in the Wikipedia entry on the substitution principle says nothing about this and does not in fact include any of the terms “assertion”, “precondition”, “postcondition” or “invariant”. To me this absence means that the article misses a key property of substitution: that the abstract semantics remain the same. (Also cited is a 1994 Liskov article in TOPLAS, but that was many years after OOSC1 and other articles explaining substitution and the assertion rules.)

Liskov’s original paper states that “if for each object o1 of type S there is an object o2 of type T such that for all programs P defined in terms of T, the behavior of P is unchanged when o1 is substituted for oz, then S is a subtype of T.” As stated, this property is impossible to satisfy: if the behavior is identical, then the implementations are the same, and the two types are identical (or differ only by name). Of course the concrete behaviors are different: applying the operation rotate to two different figures o1 and o2, whose types are subtypes of FIGURE and in some cases of each other, will trigger different algorithms — different behaviors. Only with assertions (contracts) does the substitution idea make sense: the abstract behavior, as characterized by preconditions, postconditions and the class invariants, is the same (modulo respective weakening and strengthening to preserve the flexibility of the different version). Realizing this was a major step in understanding inheritance and typing.

I do not know of any earlier (or contemporary) exposition of this principle and it would be normal to get the appropriate recognition.

Software design: design patterns

Two of the important patterns in the “Gang of Four” Design Patterns book (GoF) by Gamma et al. (1995) are the Command Pattern and the Bridge Pattern. I introduced them (under different names) in the following publications:

• The command pattern appears in OOSC1 under the name “Undo-Redo” in section 12.2. The solution is essentially the same as in GoF. I do not know of any earlier exposition of the technique. See also notes [B] and [C].

• The bridge pattern appears under the name “handle technique” in my book Reusable Software: The Base Component Libraries (Prentice Hall, 1994). It had been described several years earlier in manuals for Eiffel libraries. I do not know of an earlier reference. (The second edition of Object-Oriented Software Construction — Prentice Hall, 1997, “OOSC2” –, which also describes it, states that a similar technique is described in an article by Josef Gil and Ricardo Szmit at the TOOLS USA conference in the summer of 1994, i.e. after the publication of Reusable Software.)

Note that it is pointless to claim precedence over GoF since that book explicitly states that it is collecting known “best practices”, not introducing new ones. The relevant questions are: who, pre-GoF, introduced each of these techniques first; and which publications does the GoF cites as “prior art”  for each pattern. In the cases at hand, Command and Bridge, it does not cite OOSC1.

To be concrete: unless someone can point to an earlier reference, then anytime anyone anywhere using an interactive system enters a few “CTRL-Z” to undo commands, possibly followed by some “CTRL-Y” to redo them (or uses other UI conventions to achieve these goals), the software most likely relying on a technique that I first described in the place mentioned above.

Software design: Open-Closed Principle

Another contribution of OOSC1 (1988), section 2.3, reinforced in OOSC2 (1997) is the Open-Closed principle, which explained one of the key aspects of inheritance: the ability to keep a module both closed (immediately usable as is) and open to extension (through inheritance, preserving the basic semantics. I am mentioning this idea only in passing since in this case my contribution is usually recognized, for example in the Wikipedia entry.

Software design: OO for reuse

Reusability: the Case for Object-Oriented Design (1987) is, I believe, the first publication that clearly explained why object-oriented concepts were (and still are today — in Grady Booch’s words, “there is no other game in town”) the best answer to realize the goal of software construction from software components. In particular, the article:

• Explains the relationship between abstract data types and OO programming, showing the former as the theoretical basis for the latter. (The CLU language at MIT originated from Liskov’s pioneering work on abstract data types, but was not OO in the full sense of the term, missing in particular a concept of inheritance.)
• Shows that reusability implies bottom-up development. (Top-down refinement was the mantra at the time, and promoting bottom-up was quite a shock for many people.)
• Explains the role of inheritance for reuse, as a complement to Parnas’s interface-based modular construction with information hiding.

Software design: Design by Contract

The contribution of Design by Contract is one that is widely acknowledged so I don’t have any point to establish here — I will just recall the essentials. The notion of assertion goes back to the work of Floyd, Hoare and Dijkstra in the sixties and seventies, and correctness-by-construction to Dijktra, Gries and Wirth, but Design by Contract is a comprehensive framework providing:

• The use of assertions in an object-oriented context. (The notion of class invariant was mentioned in a paper by Tony Hoare published back in 1972.)
• The connection of inheritance with assertions (as sketched above). That part as far as I know was entirely new.
• A design methodology for quality software: the core of DbC.
• Language constructs carefully seamed into the fabric of the language. (There were precedents there, but in the form of research languages such as Alphard, a paper design only, not implemented, and Euclid.)
• A documentation methodology.
• Support for testing.
• Support for a consistent theory of exception handling (see next).

Design by Contract is sometimes taken to mean simply the addition of a few assertions here and there. What the term actually denotes is a comprehensive methodology with all the above components, tightly integrated into the programming language. Note in particular that preconditions and postconditions are not sufficient; in an OO context class invariants are essential.

Software design: exceptions

Prior to the Design by Contract work, exceptions were defined very vaguely, as something special you do outside of “normal” cases, but without defining “normal”. Design by Contract brings a proper perspective by defining these concepts precisely. This was explained in a 1987 article, Disciplined Exceptions ([86] in the list), rejected by ECOOP but circulated as a technical report; they appear again in detail in OOSC1 (sections 7.10.3 to 7.10.5).

Other important foundational work on exceptions, to which I know no real precursor (as usual I would be happy to correct any omission), addressed what happens to the outcome of an exception in a concurrent or distributed context. This work was done at ETH, in particular in the PhD theses  of B. Morandi and A. Kolesnichenko, co-supervised with S. Nanz. See the co-authored papers [345] and [363].

On the verification aspect of exceptions, see below.

Software design: refactoring

I have never seen a discussion of refactoring that refers to the detailed discussion of generalization in both of the books Reusable Software (1994, chapter 3) and Object Success (Prentice Hall, 1995, from page 122 to the end of chapter 6). These discussions describe in detail how, once a program has been shown to work, it should be subject to a posteriori design improvements. It presents several of the refactoring techniques (as they were called when the idea gained traction several years later), such as moving common elements up in the class hierarchy, and adding an abstract class as parent to concrete classes ex post facto.

These ideas are an integral part of the design methodology presented in these books (and again in OOSC2 a few later). It is beyond me why people would present refactoring (or its history, as in the Wikipedia entry on the topic) without referring to these publications, which were widely circulated and are available for anyone to inspect.

Software design: built-in documentation and Single-Product principle

Another original contribution was the idea of including documentation in the code itself and relying on tools to extract the documentation-only information (leaving implementation elements aside). The idea, described in detail in OOSC1 in 1988 (sections 9.4 and 9.5) and already mentioned in the earlier Eiffel papers, is that code should be self-complete, containing elements of various levels of abstraction; some of them describe implementation, but the higher-level elements describe specification, and are distinguished syntactically in such a way that tools can extract them to produce documentation at any desired level of abstraction.

The ideas were later applied through such mechanisms as JavaDoc (with no credit as far as I know). They were present in Eiffel from the start and the underlying principles, in particular the “Single Product principle” (sometimes “Self-Documentation principle”, and also generalized by J. Ostroff and R. Paige as “Single-Model principle”). Eiffel is the best realization of these principles thanks to:

• Contracts (as mentioned above): the “contract view” of a class (called “short form” in earlier descriptions) removes the implementations but shows the relevant preconditions, postconditions and class invariants, given a precise and abstract specification of the class.
• Eiffel syntax has a special place for “header comments”, which describe high-level properties and remain in the contract view.
• Eiffel library class documentation has always been based on specifications automatically extracted from the actual text of the classes, guaranteeing adequacy of the documentation. Several formats are supported (including, from 1995 on, HTML, so that documentation can be automatically deployed on the Web).
• Starting with the EiffelCase tool in the early 90s, and today with the Diagram Tool of EiffelStudio, class structures (inheritance and client relationships) are displayed graphically, again in an automatically extracted form, using either the BON or UML conventions.

One of the core benefits of the Single-Product principle is to guard against what some of my publications called the “Dorian Gray” syndrome: divergence of an implementation from its description, a critical problem in software because of the ease of modifying stuff. Having the documentation as an integral part of the code helps ensure that when information at some level of abstraction (specification, design, implementation) changes, the other levels will be updated as well.

Crucial in the approach is the “roundtripping” requirement: specifiers or implementers can make changes in any of the views, and have them reflected automatically in the other views. For example, you can graphically draw an arrow between two bubbles representing classes B and A in the Diagram Tool, and the code of B will be updated with “inherit A”; or you can add this Inheritance clause textually in the code of class B, and the diagram will be automatically updated with an arrow.

It is important to note how contrarian and subversive these ideas were at the time of their introduction (and still to some extent today). The wisdom was that you do requirements then design then implementation, and that code is a lowly product entirely separate from specification and documentation. Model-Driven Development perpetuates this idea (you are not supposed to modify the code, and if you do there is generally no easy way to propagate the change to the model.) Rehabilitating the code (a precursor idea to agile methods, see below) was a complete change of perspective.

I am aware of no precedent for this Single Product approach. The closest earlier ideas I can think of are in Knuth’s introduction of Literate Programming in the early eighties (with a book in 1984). As in the Single-product approach, documentation is interspersed with code. But the literate programming approach is (as presented) top-down, with English-like explanations progressively being extended with implementation elements. The Single Product approach emphasizes the primacy of code and, in terms of the design process, is very much yoyo, alternating top-down (from the specification to the implementation) and bottom-up (from the implementation to the abstraction) steps. In addition, a large part of the documentation, and often the most important one, is not informal English but formal assertions. I knew about Literate Programming, of course, and learned from it, but Single-Product is something else.

Software design: from patterns to components

Karine Arnout’s thesis at ETH Zurich, resulting in two co-authored articles ([255] and [257], showed that contrary to conventional wisdom a good proportion of the classical design patterns, including some of the most sophisticated, can be transformed into reusable components (indeed part of an Eiffel library). The agent mechanism (see below) was instrumental in achieving that result.

Programming, design and specification concepts: abstract data types

Liskov’s and Zilles’s ground-breaking 1974 abstract data types paper presented the concepts without a mathematical specification, using programming language constructs instead. A 1976 paper (number [3] in my publication list, La Description des Structures de Données, i.e. the description of data structures) was as far as I know one of the first to present a mathematical formalism, as  used today in presentations of ADTs. John Guttag was taking a similar approach in his PhD thesis at about the same time, and went further in providing a sound mathematical foundation, introducing in particular (in a 1978 paper with Jim Horning) the notion of sufficient completeness, to which I devoted a full article in this blog  (Are My Requirements Complete?) about a year ago. My own article was published in a not very well known journal and in French, so I don’t think it had much direct influence. (My later books reused some of the material.)

The three-level description approach of that article (later presented in English for an ACM workshop in the US in 1981, Pingree Park, reference [28]) is not well known but still applicable, and would be useful to avoid frequent confusions between ADT specifications and more explicit descriptions.

When I wrote my 1976 paper, I was not aware of Guttag’s ongoing work (only of the Liskov and Zilles paper), so the use of a mathematical framework with functions and predicates on them was devised independently. (I remember being quite happy when I saw what the axioms should be for a queue.) Guttag and I both gave talks at a workshop organized by the French programming language interest group in 1977 and it was fun to see that our presentations were almost identical. I think my paper still reads well today (well, if you read French). Whether or not it exerted direct influence, I am proud that it independently introduced the modern way of thinking of abstract data types as characterized by mathematical functions and their formal (predicate calculus) properties.

Language mechanisms: genericity with inheritance

Every once in a while I get to referee a paper that starts “Generics, as introduced in Java…” Well, let’s get some perspective here. Eiffel from its introduction in 1985 combined genericity and inheritance. Initially, C++ users and designers claimed that genericity was not needed in an OO context and the language did not have it; then they introduced template. Initially, the designers of Java claimed (around 1995) that genericity was not needed, and the language did not have it; a few years later Java got generics. Initially, the designers of C# (around 1999) claimed that genericity was not needed, and the language did not have it; a few years later C# and .NET got generics.

Genericity existed before Eiffel of course; what was new was the combination with inheritance. I had been influenced by work on generic modules by a French researcher, Didier Bert, which I believe influenced the design of Ada as well; Ada was the language that brought genericity to a much broader audience than the somewhat confidential languages that had such a mechanism before. But Ada was not object-oriented (it only had modules, not classes). I was passionate about object-oriented programming (at a time when it was generally considered, by the few people who had heard of it as an esoteric, academic pursuit). I started — in the context of an advanced course I was teaching at UC Santa Barbara — an investigation of how the two mechanisms relate to each other. The results were a paper at the first OOPSLA in 1986, Genericity versus Inheritance, and the design of the Eiffel type system, with a class mechanism, inheritance (single and multiple), and genericity, carefully crafted to complement each other.

With the exception of a Trellis-Owl, a  design from Digital Equipment Corporation also presented at the same OOPSLA (which never gained significant usage), there were no other OO languages with both mechanisms for several years after the Genericity versus Inheritance paper and the implementation of genericity with inheritance in Eiffel available from 1986 on. Eiffel also introduced, as far as I know, the concept of constrained genericity, the second basic mechanism for combining genericity with inheritance, described in Eiffel: The Language (Prentice Hall, 1992, section 10.8) and discussed again in OOSC2 (section 16.4 and throughout). Similar mechanisms are present in many languages today.

It was not always so. I distinctly remember people bringing their friends to our booth at some conference in the early nineties, for the sole purpose of having a good laugh with them at our poster advertising genericity with inheritance. (“What is this thing they have and no one else does? Generi-sissy-tee? Hahaha.”). A few years later, proponents of Java were pontificating that no serious language needs generics.

It is undoubtedly part of of the cycle of invention (there is a Schopenhauer citation on this, actually the only thing from Schopenhauer’s philosophy that I ever understood [D]) that people at some point will laugh at you; if it did brighten their day, why would the inventor deny them one of the little pleasures of life? But in terms of who laughs last, along the way C++ got templates, Java got generics, C# finally did too, and nowadays all typed OO languages have something of the sort.

Language mechanisms: multiple inheritance

Some readers will probably have been told that multiple inheritance is a bad thing, and hence will not count it as a contribution, but if done properly it provides a major abstraction mechanism, useful in many circumstances. Eiffel showed how to do multiple inheritance right by clearly distinguishing between features (operations) and their names, defining a class as a finite mapping between names and features, and using renaming to resolve any name clashes.

Multiple inheritance was made possible by an implementation innovation: discovering a technique (widely imitated since, including in single-inheritance contexts) to implement dynamic binding in constant time. It was universally believed at the time that multiple inheritance had a strong impact on performance, because dynamic binding implied a run-time traversal of the class inheritance structure, already bad enough for single inheritance where the structure is a tree, but prohibitive with multiple inheritance for which it is a directed acyclic graph. From its very first implementation in 1986 Eiffel used what is today known as a virtual table technique which guarantees constant-time execution of routine (method) calls with dynamic binding.

Language mechanisms: safe GC through strong static typing

Simula 67 implementations did not have automatic garbage collection, and neither had implementations of C++. The official excuse in the C++ case was methodological: C programmers are used to exerting manual control of memory usage. But the real reason was a technical impossibility resulting from the design of the language: compatibility with C precludes the provision of a good GC.

More precisely, of a sound and complete GC. A GC is sound if it will only reclaim unreachable objects; it is complete if it will reclaim all unreachable objects. With a C-based language supporting casts (e.g. between integers and pointers) and pointer arithmetic, it is impossible to achieve soundness if we aim at a reasonable level of completeness: a pointer can masquerade as an integer, only to be cast back into a pointer later on, but in the meantime the garbage collector, not recognizing it as a pointer, may have wrongly reclaimed the corresponding object. Catastrophe.

It is only possible in such a language to have a conservative GC, meaning that it renounces completeness. A conservative GC will treat as a pointer any integer whose value could possibly be a pointer (because it lies between the bounds of the program’s data addresses in memory). Then, out of precaution, the GC will refrain from reclaiming the objects at these addresses even if they appear unreachable.

This approach makes the GC sound but it is only a heuristics, and it inevitably loses completeness: every once in a while it will fail to reclaim some dead (unreachable) objects around. The result is a program with memory leaks — usually unacceptable in practice, particularly for long-running or continuously running programs where the leaks inexorably accumulate until the program starts thrashing then runs out of memory.

Smalltalk, like Lisp, made garbage collection possible, but was not a typed language and missed on the performance benefits of treating simple values like integers as a non-OO language would. Although in this case I do not at the moment have a specific bibliographic reference, I believe that it is in the context of Eiffel that the close connection between strong static typing (avoiding mechanisms such as casts and pointer arithmetic) and the possibility of sound and complete garbage collection was first clearly explained. Explained in particular around 1990 in a meeting with some of the future designers of Java, which uses a similar approach, also taken over later on by C#.

By the way, no one will laugh at you today for considering garbage collection as a kind of basic human right for programmers, but for a long time the very idea was quite sulfurous, and advocating it subjected you to a lot of scorn. Here is an extract of the review I got when I submitted the first Eiffel paper to IEEE Transactions on Software Engineering:

Systems that do automatic garbage collection and prevent the designer from doing his own memory management are not good systems for industrial-strength software engineering.

Famous last words. Another gem from another reviewer of the same paper:

I think time will show that inheritance (section 1.5.3) is a terrible idea.

Wow! I wish the anonymous reviewers would tell us what they think today. Needless to say, the paper was summarily rejected. (It later appeared in the Journal of Systems and Software — as [82] in the publication list — thanks to the enlightened views of Robert Glass, the founding editor.)

Language mechanisms: void safety

Void safety is a property of a language design that guarantees the absence of the plague of null pointer dereferencing.

The original idea came (as far as I know) from work at Microsoft Research that led to the design of a research language called C-omega; the techniques were not transferred to a full-fledged programming language. Benefiting from the existence of this proof of concept, the Eiffel design was reworked to guarantee void safety, starting from my 2005 ECOOP keynote paper (Attached Types) and reaching full type safety a few years later. This property of the language was mechanically proved in a 2016 ETH thesis by A. Kogtenkov.

Today all significant Eiffel development produces void-safe code. As far as I know this was a first among production programming languages and Eiffel remains the only production language to provide a guarantee of full void-safety.

This mechanism, carefully crafted (hint: the difficult part is initialization), is among those of which I am proudest, because in the rest of the programming world null pointer dereferencing is a major plague, threatening at any moment to crash the execution of any program that uses pointers of references. For Eiffel users it is gone.

Language mechanisms: agents/delegates/lambdas

For a long time, OO programming languages did not have a mechanism for defining objects wrapping individual operations. Eiffel’s agent facility was the first such mechanism or among the very first together the roughly contemporaneous but initially much more limited delegates of C#. The 1999 paper From calls to agents (with P. Dubois, M. Howard, M. Schweitzer and E. Stapf, [196] in the list) was as far as I know the first description of such a construct in the scientific literature.

Language mechanisms: concurrency

The 1993 Communications of the ACM paper on Systematic Concurrent Object-Oriented Programming [136] was certainly not the first concurrency proposal for OO programming (there had been pioneering work reported in particular in the 1987 book edited by Tokoro and Yonezawa), but it innovated in offering a completely data-race-free model, still a rarity today (think for example of the multi-threading mechanisms of dominant OO languages).

SCOOP, as it came to be called, was implemented a few years later and is today a standard part of Eiffel.

Language mechanisms: selective exports

Information hiding, as introduced by Parnas in his two seminal 1972 articles, distinguishes between public and secret features of a module. The first OO programming language, Simula 67, had only these two possibilities for classes and so did Ada for modules.

In building libraries of reusable components I realized early on that we need a more fine-grained mechanism. For example if class LINKED_LIST uses an auxiliary class LINKABLE to represent individual cells of a linked list (each with a value field and a “right” field containing a reference to another LINKABLE), the features of LINKABLE (such as the operation to reattach the “right” field) should not be secret, since LINKED_LIST needs them; but they should also not be generally public, since we do not want arbitrary client objects to mess around with the internal structure of the list. They should be exported selectively to LINKED_LIST only. The Eiffel syntax is simple: declare these operations in a clause of the class labeled “feature {LINKED_LIST}”.

This mechanism, known as selective exports, was introduced around 1989 (it is specified in full in Eiffel: The Language, from 1992, but was in the Eiffel manuals earlier). I think it predated the C++ “friends” mechanism which serves a similar purpose (maybe someone with knowledge of the history of C++ has the exact date). Selective exports are more general than the friends facility and similar ones in other OO languages: specifying a class as a friend means it has access to all your internals. This solution is too coarse-grained. Eiffel’s selective exports make it possible to define the specific export rights of individual operations (including attributes/fields) individually.

Language mechanisms and implementation: serialization and schema evolution

I did not invent serialization. As a student at Stanford in 1974 I had the privilege, at the AI lab, of using SAIL (Stanford Artificial Intelligence Language). SAIL was not object-oriented but included many innovative ideas; it was far ahead of its time, especially in terms of the integration of the language with (what was not yet called) its IDE. One feature of SAIL with which one could fall in love at first sight was the possibility of selecting an object and having its full dependent data structure (the entire subgraph of the object graph reached by following references from the object, recursively) stored into a file, for retrieval at the next section. After that, I never wanted again to live without such a facility, but no other language and environment had it.

Serialization was almost the first thing we implemented for Eiffel: the ability to write object.store (file) to have the entire structure from object stored into file, and the corresponding retrieval operation. OOSC1 (section 15.5) presents these mechanisms. Simula and (I think) C++ did not have anything of the sort; I am not sure about Smalltalk. Later on, of course, serialization mechanisms became a frequent component of OO environments.

Eiffel remained innovative by tackling the difficult problems: what happens when you try to retrieve an object structure and some classes have changed? Only with a coherent theoretical framework as provided in Eiffel by Design by Contract can one devise a meaningful solution. The problem and our solutions are described in detail in OOSC2 (the whole of chapter 31, particularly the section entitled “Schema evolution”). Further advances were made by Marco Piccioni in his PhD thesis at ETH and published in joint papers with him and M. Oriol, particularly [352].

Language mechanisms and implementation: safe GC through strong static typing

Simula 67 (if I remember right) did not have automatic garbage collection, and neither had C++ implementations. The official justification in the case of C++ was methodological: C programmers are used to exerting manual control of memory usage. But the real obstacle was technical: compatibility with C makes it impossible to have a good GC. More precisely, to have a sound and complete GC. A GC is sound if it will only reclaim unreachable objects; it is complete if it will reclaim all unreachable objects. With a C-based language supporting casts (e.g. between integers and pointers) and pointer arithmetic, it is impossible to achieve soundness if we aim at a reasonable level of completeness: a pointer can masquerade as an integer, only to be cast back into a pointer later on, but in the meantime the garbage collector, not recognizing it as a pointer, may have wrongly reclaimed the corresponding object. Catastrophe. It is only possible in such a language to have a conservative GC, which will treat as a pointer any integer whose value could possibly be a pointer (because its value lies between the bounds of the program’s data addresses in memory). Then, out of precaution, it will not reclaim the objects at the corresponding address. This approach makes the GC sound but it is only a heuristics, and it may be over-conservative at times, wrongly leaving dead (i.e. unreachable) objects around. The result is, inevitably, a program with memory leaks — usually unacceptable in practice.

Smalltalk, like Lisp, made garbage collection possible, but was not a typed language and missed on the performance benefits of treating simple values like integers as a non-OO language would. Although in this case I do not at the moment have a specific bibliographic reference, I believe that it is in the context of Eiffel that the close connection between strong static typing (avoiding mechanisms such as casts and pointer arithmetic) and the possibility of sound and complete garbage collection was first clearly explained. Explained in particular to some of the future designers of Java, which uses a similar approach, also taken over later on by C#.

By the way, no one will laugh at you today for considering garbage collection as a kind of basic human right for programmers, but for a long time it was quite sulfurous. Here is an extract of the review I got when I submitted the first Eiffel paper to IEEE <em>Transactions on Software Engineering:

Software engineering: primacy of code

Agile methods are widely and properly lauded for emphasizing the central role of code, against designs and other non-executable artifacts. By reading the agile literature you might be forgiven for believing that no one brought up that point before.

Object Success (1995) makes the argument very clearly. For example, chapter 3, page 43:

Code is to our industry what bread is to a baker and books to a writer. But with the waterfall code only appears late in the process; for a manager this is an unacceptable risk factor. Anyone with practical experience in software development knows how many things can go wrong once you get down to code: a brilliant design idea whose implementation turns out to require tens of megabytes of space or minutes of response time; beautiful bubbles and arrows that cannot be implemented; an operating system update, crucial to the project which comes five weeks late; an obscure bug that takes ages to be fixed. Unless you start coding early in the process, you will not be able to control your project.

Such discourse was subversive at the time; the wisdom in software engineering was that you need to specify and design a system to death before you even start coding (otherwise you are just a messy “hacker” in the sense this word had at the time). No one else in respectable software engineering circles was, as far as I know, pushing for putting code at the center, the way the above extract does.

Several years later, agile authors started making similar arguments, but I don’t know why they never referenced this earlier exposition, which still today I find not too bad. (Maybe they decided it was more effective to have a foil, the scorned Waterfall, and to claim that everyone else before was downplaying the importance of code, but that was not in fact everyone.)

Just to be clear, Agile brought many important ideas that my publications did not anticipate; but this particular one I did.

Software engineering: the roles of managers

Extreme Programming and Scrum have brought new light on the role of managers in software development. Their contributions have been important and influential, but here too they were for a significant part prefigured by a long discussion, altogether two chapters, in Object Success (1995).

To realize this, it is enough to read the titles of some of the sections in those chapters, describing roles for managers (some universal, some for a technical manager): “risk manager”, “interface with the rest of the world” (very scrummy!), “protector of the team’s sanity”, “method enforcer” (think Scrum Master), “mentor and critic”. Again, as far as I know, these were original thoughts at the time; the software engineering literature for the most part did not talk about these issues.

Software engineering: outsourcing

As far as I know the 2006 paper Offshore Development: The Unspoken Revolution in Software Engineering was the first to draw attention, in the software engineering community, to the peculiar software engineering challenges of distributed and outsourced development.

Software engineering: automatic testing

The AutoTest project (with many publications, involving I. Ciupa, A. Leitner, Y. Wei, M. Oriol, Y. Pei, M. Nordio and others) was not the first to generate tests automatically by creating numerous instances of objects and calling applicable operations (it was preceded by Korat at MIT), but it was the first one to apply this concept with Design by Contract mechanisms (without which it is of little practical value, since one must still produce test oracles manually) and the first to be integrated in a production environment (EiffelStudio).

Software engineering: make-less system building

One of the very first decisions in the design of Eiffel was to get rid of Make files.

Feldman’s Make had of course been a great innovation. Before Make, programmers had to produce executable systems manually by executing sequences of commands to compile and link the various source components. Make enabled them to instead  to define dependencies between components in a declarative way, resulting in a partial order, and then performed a topological sort to produce the sequence of comments. But preparing the list of dependencies remains a tedious task, particularly error-prone for large systems.

I decided right away in the design of Eiffel that we would never force programmers to write such dependencies: they would be automatically extracted from the code, through an exhaustive analysis of the dependencies between modules. This idea was present from the very the first Eiffel report in 1985 (reference [55] in the publication list): Eiffel programmers never need to write a Make file or equivalent (other than for non-Eiffel code, e.g. C or C++, that they want to integrate); they just click a Compile button and the compiler figures out the steps.

Behind this approach was a detailed theoretical analysis of possible relations between modules in software development (in many programming languages), published as the “Software Knowledge Base” at ICSE in 1985. That analysis was also quite instructive and I would like to return to this work and expand it.

Educational techniques: objects first

Towards an Object-Oriented Curriculum ( TOOLS conference, August 1993, see also the shorter JOOP paper in May of the same year) makes a carefully argued case for what was later called the Objects First approach to teaching programming. I would be interested to know if there are earlier publications advocating starting programming education with an OO language.

The article also advocated for the “inverted curriculum”, a term borrowed from work by Bernie Cohen about teaching electrical engineering. It was the first transposition of this concept to software education. In the article’s approach, students are given program components to use, then little by little discover how they are made. This technique met with some skepticism and resistance since the standard approach was to start from the very basics (write trivial programs), then move up. Today, of course, many introductory programming courses similarly provide students from day one with a full-fledged set of components enabling them to produce significant programs.

More recent articles on similar topics, taking advantage of actual teaching experience, are The Outside-In Method of Teaching Programming (2003) and The Inverted Curriculum in Practice (at ICSE 2006, with Michela Pedroni). The culmination of that experience is the textbook Touch of Class from 2009.

Educational techniques: Distributed Software Projects

I believe our team at ETH Zurich (including among others M. Nordio, J. Tschannen, P. Kolb and C. Estler and in collaboration with C. Ghezzi, E. Di Nitto and G. Tamburrelli at Politecnico di Milano, N. Aguirre at Rio Cuarto and many others in various universities) was the first to devise,  practice and document on a large scale (see publications and other details here) the idea of an educational software project conducted in common by student groups from different universities. It yielded a wealth of information on distributed software development and educational issues.

Educational techniques: Web-based programming exercises

There are today a number of cloud-based environments supporting the teaching of programming by enabling students to compile and test their programs on the Web, benefiting from a prepared environment (so that they don’t have to download any tools or prepare control files) and providing feedback. One of the first — I am not sure about absolute precedence — and still a leading one, used by many universities and applicable to many programming languages, is Codeboard.

The main developer, in my chair at ETH Zurich, was Christian Estler, supported in particular by M. Nordio and M. Piccioni, so I am only claiming a supporting role here.

Educational techniques: key CS/SE concepts

The 2001 paper Software Engineering in the Academy did a good job, I think, of defining the essential concepts to teach in a proper curriculum (part of what Jeannette Wing’s 2006 paper called Computational Thinking).

Program verification: agents (delegates etc.)

Reasoning about Function Objects (ICSE 2010, with M. Nordio, P. Müller and J. Tschannen) introduced verification techniques for objects representing functions (such as agents, delegates etc., see above) in an OO language. Not sure whether there were any such techniques before.

Specification languages: Z

The Z specification language has been widely used for formal development, particularly in the UK. It is the design of J-R Abrial. I may point out that I was a coauthor of the first publication on Z in English (1980),  describing a version that preceded the adaptation to a more graphical-style notation done later at Oxford. The first ever published description of Z, pertaining to an even earlier version, was in French, in my book Méthodes de Programmation (with C. Baudoin), Eyrolles, 1978, running over 15 pages (526-541), with the precise description of a refinement process.

Program verification: exceptions

Largely coming out of the PhD thesis of Martin Nordio, A Sound and Complete Program Logic for Eiffel (TOOLS 2009) introduces rules for dealing with exceptions in a Hoare-style verification framework.

Program verification: full library, and AutoProof

Nadia Polikarpova’s thesis at ETH, aided by the work of Carlo Furia and Julian Tschannen (they were the major contributors and my participation was less important), was as far as I know the first to produce a full functional verification of an actual production-quality reusable library. The library is EiffelBase 2, covering fundamental data structures.

AutoProof — available today, as a still experimental tool, through its Web interface, see here — relied on the AutoProof prover, built by the same team, and itself based on Microsoft Research’s Boogie and Z3 engines.

More

There are more concepts worthy of being included here, but for today I will stop here.

Notes

[A] One point of divergence between usual presentations of the substitution principle and the view in OOSC and my other publications is the covariance versus contravariance of routine argument types. It reflects a difference of views as to what the proper policy (both mathematically sound and practically usable) should be.

[B]  The GoF book does not cite OOSC for the command or bridge patterns. For the command pattern it cites (thanks to Adam Kosmaczewski for digging up the GoF text!) a 1985 SIGGRAPH paper by Henry Lieberman (There’s More to Menu Systems than Meets the Screen). Lieberman’s paper describes the notion of command object and mentions undoing in passing, but does not include the key elements of the command pattern (as explained in full in OOSC1), i.e. an abstract (deferred) command class with deferred procedures called (say) do_it and undo_it, then specific classes for each kind of command, each providing a specific implementation of those procedures, then a history list of commands supporting multiple-level undo and redo as explained in OOSC1. (Reading Lieberman’s paper with a 2021 perspective shows that it came tantalizingly close to the command pattern, but doesn’t get to it. The paper does talk about inheritance between command classes, but only to “define new commands as extensions to old commands”, not in the sense of a general template that can be implemented in many specific ways. And it does mention a list of objects kept around to enable recovery from accidental deletions, and states that the application can control its length, as is the case with a history list; but the objects in the list are not command objects, they are graphical and other objects that have been deleted.)

[C] Additional note on the command pattern: I vaguely remember seeing something similar to the OOSC1 technique in an article from a supplementary volume of the OOPSLA proceedings in the late eighties or early nineties, i.e. at the same time or slightly later, possibly from authors from Xerox PARC, but I have lost the reference.

[D] Correction: I just checked the source and learned that the actual Schopenhauer quote (as opposed to the one that is usually quoted) is different; it does not include the part about laughing. So much for my attempts at understanding philosophy.

Let us assume for the sake of the argument that software quality matters. There are many ingredients to software quality, of which one must be the care that every programmer devotes to the job. The Personal Software Process, developed by Watts Humphrey in the 1990s [1], prescribes a discipline that software developers should apply to produce good software and improve their professional ability over their careers. It has enjoyed moderate success but was never a mass movement and rarely gets mentioned nowadays; few software developers, in my experience, even know the name. Those who do often think of it as passé, a touching memory from the era of Monica Lewinsky and the Roseanne show.

Once cleaned of a few obsolete elements, PSP deserves to be known and applied.

PSP came out of Watts Humphrey’s earlier work on the Capability Maturity Model (see my earlier article on this blog, What is wrong with CMMI), a collection of recommended practices and assessment criteria for software processes, originally developed in the mid-eighties for the U.S. military contractor community but soon thereafter embraced by software outsourcing companies (initially, Indian ones) and later by other industries. Responding to complaints that CMM/CMMI, focused on processes in large companies, ignored the needs of smaller ones, and lacked individual guidance for developers, Humphrey developed TSP, the Team Software Process, and PSP.

The most visible part of PSP is a six-step process pictured in the middle of this diagram:

The most visible and also the most corny. Who today wants to promise always to follow such a strict sequence of steps? Always to write the code for a module in full before compiling it? (Notice there is no backward arrow, the process is sequential.) Always to test at the end only? Come on. This is the third decade of the 21st century.

Today we compile as we code, using the development environment (IDE) as a brilliant tool to check everything we do or plan to do. For my part, whenever I am writing code and have not compiled my current draft for more than a few minutes I start feeling like an addict in need of a fix; my fix is the Compile button of EiffelStudio. At some eventual stage the compiler becomes a tool to generate excutable code, but long before that it has been my friend, coach, mentor, and doppelgänger, helping me get things (types, null references, inheritance…) right and gently chiding me when I wander off the rails.

As to tests, even if you do not buy into the full dogma of Test-Driven Development (I don’t), they get written and exercised right from the start, as you are writing the code, not afterwards. Compile all the time, test all the time.

It’s not just that a process such as the above ignores the contributions of agile methods, which are largely posterior to PSP. As analyzed in [2], agile is a curious mix of good ideas and a few horrendous ones. But among its durable contributions is the realization that development must be incremental, not a strict succession of separate activities.

This old-style flavor or PSP is probably the reason why it has fallen out of favor. But (like the agile rejection of upfront lifecycle activities) such a reaction is a case of criticism gone too far, ignoring the truly beneficial contributions. Ignore PSP’s outmoded sequence of activities and you will find that PSP’s core message is as relevant today as it ever was. That message is: we should learn from the practices of traditional engineers and apply a strict professional discipline. For example:

• Keep a log of all activities. (See “Logs” in the above figure.) Engineers are taught to record everything they do; many programmers don’t bother. This practice, however, is essential to self-improvement.
• Keep measurements of everything you do. (There are lots of things to measure, from hours spent on every kind of task to bugs found, time to fix them etc.)
• Estimate and plan your work.
• Clearly define commitments, and meet them.
• Resist pressure to make unreasonable commitments (something that agilists approach also emphasize).
• Understand your current performance.
• Understand your programming style and how it affects various measures. (As an example, code size, as a function of the number of routines, depends on whether you are more concise or more verbose in style).
• Continually improve your expertise as a professional.

PSP does not limit itself to such exhortations but gives concrete tools to apply the principles, with a view to: measuring, tracking and analyzing your work; learning from your performance variations; and incorporating the lessons learned into your professional practices. On the topic of measurement, for example, PSP includes precise guidelines on what to measure and how to measure it, and how to rely on proxies for quantities that are hard to assess directly. On this last point, PSP includes PROBE (PROxy-Based Estimating, you cannot have a method coming out of the world of US government organizations without cringeworthy acronyms), a general framework for estimating size and resource parameters from directly measurable proxies.

This is what PSP is about: a discipline of personal productivity and growth, emphasizing personal discipline, tracking and constant improvement. It is not hard to learn; a technical report by Humphrey available online [3] provides a sufficient basis to understand the concepts and start a process of self-improvement.

Watts Humphrey himself, as all who had the privilege to meet him can testify, was a model of seriousness and professionalism, the quintessential engineer. (I also remember him as the author of what may be the best pun I ever heard — ask me sometime.) PSP directly reflects these qualities and — ignoring its visible but in the end unimportant remnants from outdated technical choices — should be part of every software engineering curriculum and every software engineer’s collection of fundamental practices.

References

[1] Watts Humphrey, Introduction to the Personal Software Process, Addison-Wesley, 1996.

[2] Bertrand Meyer: Agile! The Good, the Hype and the Ugly, Springer, 2014, see here.

[3] Watts Humphrey, The Personal Software Process, Software Engineering Institute Technical Report CMU/SEI-2000-TR-022, available (in PDF, free) here.

A version of this article was first published in the Communications of the ACM blog.

.

I have been conducting interesting conversations with a two-something child who has not quite mastered the speaker-dependent [1] personal pronouns. He says things like “Where is your mom?”, when he actually means to ask about his mother, not mine; from hearing people tell him things like “your mom is coming”, he is clearly taking “your mom” as some kind of paraphrase for “mom”. He approaches people and says “I want to help me”, obviously from having heard, from others, “would you come and help me?”.

I am not concerned about young Tim (let us call him that), who sooner or later will get the point. But let us assume that someone, call him Tom, is determined to explain to Tim the concepts of “you” and “me”. Not so easy! In fact, come to think of it, fairly tricky, treacherous even. We all learned the concept at some point; I wish I remembered how it happened for me [2].

The difficulty is that someone, whether Tom or a third party, has to provide the explanation, a circumstance that messes up the explanation itself since it contains speaker-dependent terms. (Did I hear the word “Heisenberg”? If so I will ignore it.) Tom might try something like the following explanation — let us call it /A/  — but it will not work:

If Tom says me it means Tom, but if Tim says me it means Tim.

If Tim says you it means Tom, but if Tom says you it means Tim.

The reason it does not work is lack of quoting, but before I get to this let me mention that a mathematical model is not hard to come by. From a two-element set Names = {Tim, Tom} to itself, there are four total functions. Of these, two are constant functions. The other two are non-constant; one, me, is the identity function on Names, and you is the other. They are the functions me = {<Tim, Tim>, <Tom, Tom>} and you = {<Tim, Tom>, <Tom, Tim>}. I is just a synonym for me (the accusative in the latter being one of the few remnants of declension in English.)

Let us call this explanation /B/.  It can be illustrated as follows:

We can also write these functions (using for conciseness [c: A \ d: B … \ Z] for the conditional expression if c then A elseif d then B … else Z end) as the following version /C/:

me = λ n | [n = Tim: Tim \ Tom]

you = λ n | [n = Tim: Tom \ Tim]

In practice, however, this modeling of the concepts “you” and “me” as functions in Names → Names is not sufficient to define them properly, for example to turn the informal explanation /A/ into one that makes sense. The problem is that we are dealing with a larger set of words than just Names: the set   Words = {Tim, Tom, Me, You} with four elements. The meaning of a sentence that may include any of them is not absolute, but depends on who is uttering the sentence. When I say “me” and you say “me” the meaning is different, although when I say “you” and you say “me” the meaning is the same.

To interpret a sentence, then, we need a second-level function: a function meaning not in Words → Words but in Names → Words → Names, defined as follows:

meaning = λ n  |  λ w  |     [w ∈ Names: w    \    w = Me: me (n)    \    you (n)]

Let us call this definition /D/. Examples of its application include:

• meaning (Tim) (Tom) = Tom. (First case: no speaker-dependency).
• meaning (Tim) (Me) = Tim. (Second case, expresses the part of /A/ that said “if Tim says me it means Tim”.)
• meaning (Tim) (You) = Tom. (Third case, expresses the part of /A/ that said “if Tim says you it means Tom”.)

/D/ is the most accurate definition of speaker-dependent pronouns and I may try it with the real Tim at the next opportunity (as soon as I have taught him lambda calculus).

/D/ also helps us understand what does not quite work in /A/, the first and perhaps most intuitive attempt. With explanations such as  “if Tim says you it means Tom” we are actually trying to express the need for making meanings speaker-dependent, that is to say, explain that the evaluation of a sentence must take into account who utters it. But this attempt fails because we need a general rule which will apply to all sentences, and the explanation itself is a sentence. To evaluate the sentence “if Tim says you it means Tom” we need to evaluate “you” which figures in it; that evaluation would yield either Tim or Tom depending on who is speaking. But because the sentence is itself part a definition of “you”, we do not want in this case to evaluate “you”.

We could write you in straight quotes as in programming languages:

if Tim says “you” it means Tom

but that is not the form of quoting we need. In a programming language, “you” is a character string, made of the characters ‘y‘, ‘o‘ and ‘u‘ in that order. Here, the makeup of this string in terms of its characters is completely irrelevant. The form of quoting that we need must achieve something else: preventing, in the evaluation of a formula, the evaluation of one of its parts.

John McCarthy’s Lisp language, coming out as early as 1959, showed how to handle this issue correctly. (This contribution is one of many from Lisp, including garbage collection and the notion of functional programming — not bad for a single language. See my 2011 obituary of John McCarthy on this blog [3].) One of the reasons Lisp needed a quoting mechanism is that it was designed to be self-describing and specifically self-evaluating, a spectacularly new concept at the time. McCarthy’s original book on Lisp (LISP 1.5 Programmer’s Manual, MIT Press, 1962) contains a dazzling interpreter of Lisp, written in Lisp and taking up no more than half a page. The interpreter is based on eval, a function (in the sense of a Lisp function, defined by a Lisp expression) which evaluates any Lisp program. You cannot define eval unless you have some way to prevent evaluation of part of an expression.

The convention is simple. For any expression x we may define another expression ‘x — which we can read aloud as “QUOTED x”. Then:

• Evaluating x yields the value of x.
• Evaluating ‘x yields x.

The original Lisp notation was (QUOTE x), which clearly conveys the idea: QUOTE is a function — in Lisp, function application f (x) is written (f x) — whose value, when applied to an argument, is that argument. (Not the value of the argument: the argument itself.)

With such a quote notation, explanations in the style of /A/ can be made meaningful; for example (version /E/):

If Tom says ‘me it means Tom, but if Tim says ‘me it means Tim.

This should be said with the quote spoken out loud: “QUOTED me”.

We’ll see if Tim sees what /E/ means. At least, you see what you mean. I mean, I see what I  mean. Sorry, I meant that I see what you mean. Oh well. We see what we mean.

Notes and references

[1] I really want to call them “subjective personal pronouns”, in the ordinary sense of “subjective” opposed to “objective” as in “a subjective assessment”, but in grammatical terminology “subjective pronoun” has a well-accepted but entirely different meaning, that of a pronoun used as the subject of a sentence, like “she” rather than “her”. Hence “speaker-dependent pronoun”. Linguists also use the term “indexical pronouns”, as in the reference cited in note [2].

[2] Linguists investigating language learning have studied the matter. A recent article (2015) is 2-Year-Olds’ Comprehension of Personal Pronouns by M. Moyer, K. Harrigan, V. Hacquard and J. Lidz (in Supplement to the proceedings of the 39th Boston University Conference on Language Development, eds E. Grillo, K. Jepson and M. LaMendola), available here. The article includes a literature review. It acknowledges the you-and-me problem (first- and second-person pronouns) although it suggests that third-person pronouns (“he”, “she”) may be even more of a challenge to infants. Two quotes (with bibliographic references removed):

• The evidence from previous studies examining two year olds’ competence is mixed, with some studies finding children succeeding with pronouns as early as 22-24 months, others finding success much later, and some with children succeeding at a range of ages.
• Most [studies] suggest a production/comprehension asymmetry… Production studies suggest that children begin producing pronouns around 15-18 months, starting with first person, then second person, and finally third person pronouns. These early productions typically include some errors where the child reverses first and second person, but on the whole consistent errors are few . On the other hand, comprehension data focusing on speech addressed to the child suggest that children first understand second person pronouns, then first person, and finally third person.

[3] My article on John McCarthy can be found here.

I have started a new series of video lectures, which I call “Meyer’s Object-Oriented Classes” (MOOC). The goal is to share insights I have gained over the years on various aspects of programming and software engineering. Many presentations are focused on one area, such as coding, design, analysis, theoretical computer science (even there you find a division between “Theory A”, i.e. complexity, Turing machines and the like, and “Theory B”, i.e. semantics, type theory etc.), software project management, concurrency… I have an interest in all and try to explain connections.

The first lecture describes the edit distance (Levenshtein) algorithm, explains its correctness by introducing the loop invariant, expands on that notion, then shows a recursive version, explores the connection with the original version (it’s the invariant), and probes further into another view of recursive computations, leading to the concept of dynamic programming.

The videos are on YouTube and can be accessed from bertrandmeyer.com/levenshtein. (The general page for all lectures is at bertrandmeyer.com/mooc.)

The lecture is recorded in four segments of about 15 minutes each. In the future I will limit myself to 8-10 minutes. In fact I may record this lecture again; for example it would be better if I had a live audience rather than talking to my screen, and in general the recording is somewhat low-tech, but circumstances command. Also, I will correct a few hiccups (at some point in the recording I notice a typo on a slide and fix it on the fly), but the content will remain the same.

Feedback is of course welcome. I hope to record about a lecture a week from now on.

What can you do to or with an algorithm? In other words, what is a good verb to substitute for the hyphen in   “— the algorithm”?

You can learn an algorithm. Discovering classical algorithms is a large part of the Bildungsroman of a computer scientist. Sorting algorithms, graph algorithms, parsing algorithms, numerical algorithms, matrix algorithms, graphical algorithms…

You can teach an algorithm. Whether a professor or just a team leader, you explain to others why the obvious solution is not always the right one. As when  I saw that someone had implemented the traversal part of a garbage collection scheme (the “mark” of mark-and-sweep) using a recursive algorithm. Recursion is a great tool, but not here: it needs a stack of unpredictable size, and garbage collection, which you trigger when you run out of space, is not precisely the moment to start wildly allocating memory. In comes the Deutsch-Schorr-Waite algorithm, which improbably (as if tightrope-walking) subverts the structure itself to find its way forth and back.

To teach it, you can dance an algorithm. Sounds strange, but Informatics Europe gave its 2013 education award to the “AlgoRhythmics” group from at Sapientia University in Romania, which  demonstrates algorithms using central-European dances; see their rendering of Merge Sort:

(Their page has more examples. I see that recently they expanded to other kinds of dance and will let you discover binary search as flamenco and backtracking as classical ballet.) More generally you can simulate or animate an algorithm.

You can admire an algorithm. Many indeed are a source of wonder. The inner beauty of topological sort, Levenshtein or AVL can leave no one indifferent.

You can improve an algorithm. At least you can try.

You can invent an algorithm. Small or large, ambitious or mundane, but not imagined yet by anyone. Devising a new algorithm is a sort of rite of passage in our profession. If it does prove elegant, useful and elegant, you’ll get a real kick (trust me). Then you can publish the algorithm.

You can prove an algorithm, that is to say, mathematically establish its correctness. It is indeed increasingly unreasonable to publish an algorithm without correctness arguments. Maybe I have an excuse here to advertize for an an article that examines important algorithms across a wide variety of fields and showcases their main claim to correctness: their loop invariants.

You can implement an algorithm. That is much of what we do in software engineering, even if as an OO guy I would immediately add “as part of the associated data structure”.

Of late, algorithms have come to be associated with yet another verb; one that I would definitely not have envisioned when first learning about algorithms in Knuth (the book) and from Knuth (the man — who most certainly does not use foul language).

You can fuck an algorithm.

Thousands of British students marched recently to that slogan:

chants of “fuck the algorithm” as a speaker talks of losing her place at medical school because she was downgraded. pic.twitter.com/P15jpuBscB

— huck (@HUCKmagazine) August 16, 2020

They were demonstrating against a formula (the Guardian gives the details) that decided on university admissions. The starting point for these events was a ministerial decision to select students not from their grades at exams (“A-level”), which could not take place because of Covid, but instead from their assessed performance in their schools. So far so good but the authorities decided to calibrate these results with parameters deduced from each school’s past performance. Your grade is no longer your grade: if Jill and Joan both got a B, but Jill’s school has been better at getting students into (say) Oxford in the past, then Jill’s B is worth more than Joan’s B.

The outcry was easy to predict, or should have been for a more savvy government. Students want to be judged by their own performance, not by the results of some other students they do not even know. Arguments that the sole concern was a legimitate one (an effort to compensate for possible grade inflation in some schools) ceased to be credible when it came out that on average the algorithm boosted grades from private schools by 4.7. No theoretical justification was going to be of much comfort anyway to the many students who had been admitted to the universities of their dreams on the basis of their raw grades, and after the adjustment found themselves rejected.

In the end, “Fuck the Algorithm!” worked. The government withdrew the whole scheme; it tried to lay the blame for the fiasco on the regulatory authority (Ofqual), fooling no one.

These U.K. events of August 2020 will mark a turning point in the relationship between computer science and society. Not for the revelation that our technical choices have human consequences; that is old news, even if we often pretend to ignore it. Not for the use of Information Technology as an excuse; it is as old (“Sorry, the computer does not allow that!”) as IT itself. What “Fuck the Algorithm!” highlights is the massive danger of the current rush to apply machine learning to everything.

As long as we are talking marketing campaigns (“customers who bought the product you just ordered also bought …”) or image recognition, the admiring mood remains appropriate. But now, ever more often, machine learning (usually presented as “Artificial Intelligence” to sound more impressive) gets applied to decisions affecting human lives. In the US, for example, machine-learning algorithms increasingly help judges make decisions, or make the decisions themselves. Following this slippery path is crazy and unethical. It is also dangerous, as the U.K. students’ reaction indicates.

Machine learning does what the name indicates: it reproduces and generalizes the dominant behaviors of the past. The algorithms have no notion of right and wrong; they just learn. When they affect societal issues, the potential for societal disaster is everywhere.

Amid all the enthusiasm generated by the elegant techniques invented by machine-learning pioneers over the last two decades, one barely encounters any serious reservation. Codes of ethics (from ACM and others) have little to contribute.

We should be careful, though. Either we get our act together and define exacting controls on the use of machine learning for matters affecting people’s fates, or we will see a massive rejection of algorithmic technology, the right parts along with the wrong ones.

The British students of the year 2020’s weird summer will not be the last ones to tell us to fuck the algorithm.

This article was first published in the Communications of the ACM blog.

The Schaffhausen Institute of Technology (SIT) is holding a Webinar tomorrow with a set of three talks by: Serguei Beloussov, founder of Acronis and president of SIT; Michael Widenius, CTO of MariaDB and creator of MySQL Server; and Mauro Pezzè, my colleague at SIT, who will present the new master program that we have just announced, combining CS/SE topics with management and marketing courses to train future technology leaders.

The talks are in the form of a Webinar, starting at 9 AM this Tuesday (9 June). You can find all the details on the corresponding SIT page at here.

My group, the Chair of Software Engineering, at the newly created Schaffhausen Institute of Technology has open positions for both PhD students and postdocs. We are looking for candidates with a passion for reliable software and a mix of theoretical knowledge and practical experience in software engineering. Candidates should have degrees in computer science or related fields: a doctorate for postdoc positions, a master’s degree for PhD positions. Postdoc candidates should have a substantial publication record. Experience in one or more of the following fields is a plus:

• Software verification (axiomatic, model-checking, abstract interpretation etc.).
• Advanced techniques of software testing.
• Formal methods, semantics of programming languages, type theory.
• Design by Contract, Eiffel, techniques of correctness-by-construction.
• Cybersecurity.

 Compensation at both levels is attractive. The PhD program is conducted in cooperation with partner universities. 

 Interested candidates should send a CV and relevant documents or links to bm@sit.org. They are also welcome to contact me for details.

Another completely unexpected gem from the Viaje de Turquia (see the previous article on this blog): a 16-th century statement of the Dunning-Kruger effect!

An effect, of course, which has never been more visible than today (just watch the news).

Against Pedro, who narrates his travels and travails, the dialog sets two other characters, friends from his youth. They serve both as foils for Pedro, enabling his cleverness to shine — they are themselves not the brightest candles on the cake —, and as the embodiment of conventional wisdom. He occasionally gets really impatient with them, although always friendly, and at some point cites this ditty that he remembers from his youth in Spain:

Blind people want to see,

The deaf man wants to hear,

The fat man wants to slim,

The lame man wants to run.

For the fool there is no remedy:

Since he fancies that he knows,

He does not care to learn more.

Wow!

At this gloomy moment it is good to find a gem in an unexpected place.

I am reading (in translation) the Viaje de Turquia, or Turkish Voyage — literaly, Voyage of Turkey — a 16th-century epic dialog, whose authorship is disputed. It is a precious source of information on the period and rings throughout like a true story. The hero, Pedro, tells of his time as a prisoner of war of the Turks and the ignominies he had to suffer for years. He is a doctor, if a self-taught one, and has cured many members of the Pasha’s entourage, but at some point the Pasha, out of spite, sends him back to the harshest form of manual labor. One of his former patients, rich and high-ranked, spots him, the intellectual struggling to move heavy materials in the dirt and under the whip, and mocks him:

Hey, all the philosophy of Aristotle and Plato, all the medical science of Galen, all the eloquence of Cicero and Demosthenes, how have they helped you?

To which Pedro, having put his sack on his shoulder and wiped the tears caused by this pique, answers, looking him straight in the eye:

They have helped me live through days like this one.

Pretty good, I thought. Not just the sense of repartee, but the sentiment itself (echoing by the comments of many a mistreated intellectual in later ages including ours).

Not only that, but it worked, at least for a while. So astounded was the persecutor by the retort, that he took Pedro’s sack to carry it himself, and convinced the Pasha to relieve Pedro from hard work and give him money.

“We’re a group of cousins aged 8-14 who” got “the idea to help others, since we know we are not alone”. They are providing mostly free tutoring to other kids. Details here.

About this article: it originated as a series of posts on the Communications of the ACM blog. I normally repost such articles here. (Even though copy-paste is usually not good, there are three reasons for this duplication: the readership seems to be largely disjoint; I can use better formatting, since their blog software is more restrictive than WordPress; and it is good to have a single repository for all my articles, including both those who originated on CACM and those who did not.) The series took the form of nine articles, where each of the first few ended with a quiz, to which the next one, published a couple of days later, provided an answer. Since all these answers are now available it would make no sense to use the same scheme, so I am instead publishing the whole thing as a single article  with nine sections, slightly adapted from the original.

I was too lazy so far to collect all the references into a single list, so numbers such as [1] refer to the list at the end of the corresponding section.

A colleague recently asked me to present a short overview of  axiomatic semantics as a guest lecture in one of his courses. I have been teaching courses on software verification for a long time (see e.g. here), so I have plenty of material; but instead of just reusing it, I decided to spend a bit of time on explaining why it is good to have a systematic approach to software verification. Here is the resulting tutorial.

1. Introduction and attempt #1

Say “software verification” to software professionals, or computer science students outside of a few elite departments, and most of them will think  “testing”. In a job interview, for example, show a loop-based algorithm to a programmer and ask “how would you verify it?”: most will start talking about devising clever test cases.

Far from me to berate testing [1]; in fact, I have always thought that the inevitable Dijkstra quote about testing — that it can only show the presence of errors, not their absence [2] — which everyone seems to take as an indictment and dismissal of testing (and which its author probably intended that way) is actually a fantastic advertisement for testing: a way to find bugs? Yes! Great! Where do I get it?  But that is not the same as verifying the software, which means attempting to ascertain that it has no bugs.

Until listeners realize that verification cannot just mean testing, the best course material on axiomatic semantics or other proof techniques will not attract any interest. In fact, there is somewhere a video of a talk by the great testing and public-speaking guru James Whittaker where he starts by telling his audience not to worry, this won’t be a standard boring lecture, he will not start talking about loop invariants [3]! (Loop invariants are coming in this article, in fact they are one of its central concepts, but in later sections only, so don’t bring the sleeping bags yet.) I decided to start my lecture by giving an example of what happens when you do not use proper verification. More than one example, in fact, as you will see.

A warning about this article: there is nothing new here. I am using an example from my 1990 book Introduction to the Theory of Programming Languages (exercise 9.12). Going even further back, a 1983 “Programming Pearls” Communications of the ACM article by Jon Bentley [4] addresses the same example with the same basic ideas. Yet almost forty years later these ideas are still not widely known among practitioners. So consider these articles as yet another tutorial on fundamental software engineering stuff.

The tutorial is a quiz. We start with a program text:

from

i := 1 ; j := n              — Result initialized to 0.

until i = j loop

m := (i + j) // 2         — Integer division

if t [m] ≤ x then i := m  else  j := m end

end

if x = t [i] then Result := i end

All variables are of integer type. t is an up-sorted array of integers, indexed from 1 to n . We do not let any notation get between friends. A loop from p until e loop q end executes p then, repeatedly: stops if e (the exit condition) is true, otherwise executes q. (Like {p ; while not e do {q}} in some other notations.) “:=” is assignment, “=” equality testing.  “//” is integer division, e.g. 6 //3 = 7 //3 = 2. Result is the name of a special variable whose final value will be returned by this computation (as part of a function, but we only look at the body). Result is automatically initialized to zero like all integer variables, so if execution does not assign anything to Result the function will return zero.

First question: what is this program trying to do?

OK, this is not the real quiz. I assume you know the answer: it is an attempt at “binary search”, which finds an element in the array, or determines its absence, in a sequence of about log₂ (n) steps, rather than n if we were use sequential search.  (Remember we assume the array is sorted.) Result should give us a position where x appears in the array, if it does, and otherwise be zero.

Now for the real quiz: does this program meet this goal?

The answer should be either yes or no. (If no, I am not asking for a correct version, at least not yet, and in any case you can find some in the literature.) The situation is very non-symmetric, we might say Popperian:

• To justify a no answer it suffices of a single example, a particular array t and a particular value x, for which the program fails to set Result as it should.
• To justify a yes answer we need to provide a credible argument that for every t and  x the program sets Result as it should.

Notes to section 1

[1] The TAP conference series (Tests And Proofs), which Yuri Gurevich and I started, explores the complementarity between the two approaches.

[2] Dijkstra first published his observation in 1969. He did not need consider the case of infinite input sets: even for a trivial finite program that multiplies two 32-bit integers, the number of cases to be examined, 2⁶⁴, is beyond human reach. More so today with 64-bit integers. Looking at this from a 2020 perspective, we may note that exhaustive testing of a finite set of cases, which Dijkstra dismissed as impossible in practice, is in fact exactly what the respected model checking verification technique does; not on the original program, but on a simplified — abstracted — version precisely designed to keep the number of cases tractable. Dijkstra’s argument remains valid, of course, for  the original program if non-trivial. And model-checking does not get us out of the woods: while we are safe if its “testing” finds no bug, if it does find one we have to ensure that the bug is a property of the original program rather than an artifact of the abstraction process.

[3] It is somewhere on YouTube, although I cannot find it right now.

[4] Jon Bentley: Programming Pearls: Writing Correct Programs, in Communications of the ACM, vol. 26, no. 12, pp. 1040-1045, December 1983, available for example here.

2. Attempt #2

Was program #1 correct? If so it should yield the correct answer. (An answer is correct if either Result is the index in t of an element equal to x, or Result = 0 and x does not appear in t.)

This program is not correct. To prove that it is not correct it suffices of a single example (test case) for which the program does not  “yield the correct answer”. Assume x = 1 and the array t has two elements both equal to zero (n = 2, remember that arrays are indexed from 1):

t = [0   0]

The successive values of the variables and expressions are:

                                            m       i          j            i + j + 1

After initialization:                   1         2                3

i ≠ j, so enter loop:           1       1        2                 6         — First branch of “if” since t [1] ≤ x
— so i gets assigned the value of m

But then neither of the values of i and j has changed, so the loop will repeat its body identically (taking the first branch) forever. It is not even that the program yields an incorrect answer: it does not yield an answer at all!

Note (in reference to the famous Dijkstra quote mentioned in the first article), that while it is common to pit tests against proofs, a test can actually be a proof: a test that fails is a proof that the program is incorrect. As valid as the most complex mathematical proof. It may not be the kind of proof we like most (our customers tend to prefer a guarantee that the program is correct), but it is a proof all right.

We are now ready for the second attempt:

—  Program attempt #2.

from

i := 1 ; j := n

until i = j or Result > 0  loop

m := (i + j) // 2         — Integer division

if t [m] ≤ x then

i := m  + 1

elseif t [m] = x then

Result := m

else                         — In this case t [m] > x

j := m – 1

end

end

Unlike the previous one this version always changes i or j, so we may hope it does not loop forever. It has a nice symmetry between i and j.

Same question as before: does this program meet its goal?

3. Attempt #3

The question about program #2, as about program #1: was: it right?

Again no.  A trivial example disproves it: n = 1, the array t contains a single element t [1] = 0, x = 0. Then the initialization sets both i and j to 1, i = j holds on entry to the loop which stops immediately, but Result is zero whereas it should be 1 (the place where x appears).

Here now is attempt #3, let us see it if fares better:

—  Program attempt #3.

from

i := 1 ; j := n

until i = j loop

m := (i + j + 1) // 2

if t [m] ≤ x then

i := m  + 1

else

j := m

end

end

if 1  ≤ i  and i ≤ n then Result := i end
       — If not, Result remains 0.

What about this one?

3. Attempt #4 (also includes 3′)

The first two program attempts were wrong. What about the third?

I know, you have every right to be upset at me, but the answer is no once more.

Consider a two-element array t = [0 0] (so n = 2, remember that our arrays are indexed from 1 by convention) and a search value x = 1. The successive values of the variables and expressions are:

                                                  m          i          j            i + j + 1

After initialization:                            1        2           4

i ≠ j, so enter loop:               2           3        2          6                  — First branch of “if” since t [2] < x

i ≠ j,  enter loop again:        3           ⚠                                       — Out-of-bounds memory access!
— (trying to access non-existent t [3])

Oops!

Note that we could hope to get rid of the array overflow by initializing i to 0 rather than 1. This variant (version #3′) is left as a bonus question to the patient reader. (Hint: it is also not correct. Find a counter-example.)

OK, this has to end at some point. What about the following version (#4): is it right?

—  Program attempt #4.

from

i := 0 ; j := n + 1

until i = j loop

m := (i + j) // 2

if t [m] ≤ x then

i := m  + 1

else

j := m

end

end

if 1 ≤ i  and i ≤ n then Result := i end

5. Attempt #5

Yes, I know, this is dragging on. But that’s part of the idea: witnessing how hard it is to get a program right if you just judging by the seat of your pants. Maybe we can get it right this time?

Are we there yet? Is program attempt #4 finally correct?

Sorry to disappoint, but no. Consider a two-element array t = [0 0], so n = 2, and a search value x = 1 (yes, same counter-example as last time, although here we could also use x = 0). The successive values of the variables and expressions are:

                                                 m          i          j            i + j

After initialization:                           0        3           3

i ≠ j, so enter loop:               1           2       3          5            — First branch of “if”

i ≠ j, enter loop again:         2         3        3         6            — First branch again

i = j, exit loop

The condition of the final “if” is true, so Result gets the value 3. This is quite wrong, since there is no element at position 3, and in any case x does not appear in t.

But we are so close! Something like this should work, should it not?

So patience, patience, let us tweak it just one trifle more, OK?

—  Program attempt #5.

from

i := 1 ; j := n + 1

until i ≥ j or Result > 0 loop

m := (i + j) // 2

if t [m] < x then

i := m + 1

elseif  t [m] > x then

j := m

else

Result := m

end

end

Does it work now?

6. Attempt #6

The question about program #5  was the same as before: is it right, is it wrong?

Well, I know you are growing more upset at me with each section, but the answer is still that this program is wrong. But the way it is wrong is somewhat specific; and it applies, in fact, to all previous variants as well.

This particular wrongness (fancy word for “bug”) has a history. As I pointed out in the first article, there is a long tradition of using binary search to illustrate software correctness issues. A number of versions were published and proved correct, including one in the justly admired Programming Pearls series by Jon Bentley. Then in 2006 Joshua Bloch, then at Google, published a now legendary blog article [2] which showed that all these versions suffered from a major flaw: to obtain m, the approximate mid-point between i and j, they compute

(i + j) // 2

which, working on computer integers rather than mathematical integers, might overflow! This in a situation in which both i and j, and hence m as well, are well within the range of the computer’s representable integers, 2^-n to 2ⁿ (give or take 1) where n is typically 31 or, these days, 63, so that there is no conceptual justification for the overflow.

In the specification that I have used for this article, i starts at 1, so the problem will only arise for an array that occupies half of the memory or more, which is a rather extreme case (but still should be handled properly). In the general case, it is often useful to use arrays with arbitrary bounds (as in Eiffel), so we can have even a small array, with high indices, for which the computation will produce an overflow and bad results.

The Bloch gotcha is a stark reminder that in considering the correctness of programs we must include all relevant aspects and consider programs as they are executed on a real computer, not as we wish they were executed in an ideal model world.

(Note that Jon Bentley alluded to this requirement in his original article: while he did not explicitly mention integer overflow, he felt it necessary to complement his proof by the comment that that  “As laborious as our proof of binary search was, it is still unfinished by some standards. How would you prove that the program is free of runtime errors (such as division by zero, word overflow, or array indices out of bounds)?” Prescient words!)

It is easy to correct the potential arithmetic overflow bug: instead of (i + j) // 2, Bloch suggested we compute the average as

i + (j – i) // 2

which is the same from a mathematician’s viewpoint, and indeed will compute the same value if both variants compute one, but will not overflow if both i and j are within range.

So we are ready for version 6, which is the same as version 5 save for that single change:

—  Program attempt #6.

from

i := 1 ; j := n + 1

until i ≥ j or Result > 0 loop

m := i + (j – i) // 2

if t [m] < x then

i := m + 1

elseif  t [m] > x then

j := m

else

Result := m

end

end

Now is probably the right time to recall the words by which Donald Knuth introduces binary search in the original 1973 tome on Sorting and Searching of his seminal book series The Art of Computer Programming:

Although the basic idea of binary search is comparatively straightforward, the details can be somewhat tricky, and many good programmers have done it wrong the first few times they tried.

Do you need more convincing? Be careful what you answer, I have more variants up my sleeve and can come up with many more almost-right-but-actually-wrong program attempts if you nudge me. But OK, even the best things have an end. This is not the last section yet, but that was the last program attempt. To the naturally following next question in this running quiz,  “is version 6 right or wrong”, I can provide the answer: it is, to the best of my knowledge, a correct program. Yes! [3].

But the quiz continues. Since answers to the previous questions were all  that the programs were not correct, it sufficed in each case to find one case for which the program did not behave as expected. Our next question is of a different nature: can you find an argument why version #6 is correct?

References for section 6

[1] (In particular) Jon Bentley: Programming Pearls — Writing Correct Programs, in Communications of the ACM, vol. 26, no. 12, December 1983, pages 1040-1045, available here.

[2] Joshua Bloch: Extra, Extra — Read All About It: Nearly All Binary Searches and Mergesorts are Broken, blog post, on the Google AI Blog, 2 June 2006, available here.

[3] A caveat: the program is correct barring any typos or copy-paste errors — I am starting from rigorously verified programs (see the next posts), but the blogging system’s UI and text processing facilities are not the best possible for entering precise technical text such as code. However carefully I check, I cannot rule out a clerical mistake, which of course would be corrected as soon as it is identified.

7. Using a program prover

Preceding sections presented candidate binary search algorithms and asked whether they are correct. “Correct” means something quite precise: that for an array t and a value x, the final value of the variable Result is a valid index of t (that is to say, is between 1 and n, the size of t) if and only if x appears at that index in t.

The last section boldly stated that program attempt #6 was correct. The question was: why?

In the case of the preceding versions, which were incorrect, you could prove that property, and I do mean prove, simply by exhibiting a single counter-example: a single t and x for which the program does not correctly set Result. Now that I asserting the program to be correct, one example, or a million examples, do not suffice. In fact they are almost irrelevant. Test as much as you like and get correct results every time, you cannot get rid of the gnawing fear that if you had just tested one more time after the millionth test you would have produced a failure. Since the set of possible tests is infinite there is no solution in sight [1].

We need a proof.

I am going to explain that proof in the next section, but before that I would like to give you an opportunity to look at the proof by yourself. I wrote in one of the earlier articles that most of what I have to say was already present in Jon Bentley’s 1983 Programming Pearls contribution [2], but a dramatic change did occur in the four decades since: the appearance of automated proof system that can handle significant, realistic programs. One such system, AutoProof, was developed at the Chair of Software engineering at ETH Zurich [3] (key project members were Carlo Furia, Martin Nordio, Nadia Polikarpova and Julian Tschannen, with initial contributions by Bernd Schoeller) on the basis of the Boogie proof technology from Microsoft Research).

AutoProof is available for online use, and it turns out that one of the basic tutorial examples is binary search. You can go to the corresponding page and run the proof.

I am going to let you try this out (and, if you are curious, other online AutoProof examples as well) without too many explanations; those will come in the next section. Let me simply name the basic proof technique: loop invariant. A loop invariant is a property INV associated with a loop, such that:

• A. After the loop’s initialization, INV will hold.
• B. One execution of the loop’s body, if started with INV satisfied (and the loop’s exit condition not satisfied, otherwise we wouldn’t be executing the body!), satisfies INV again when it terminates.

This idea is of course the same as that of a proof by induction in mathematics: the initialization corresponds to the base step (proving that P (0) holds) and the body property to the induction step (proving that from P (n) follows P (n + 1). With a traditional induction proof we deduce that the property (P (n)) holds for all integers. For the loop, we deduce that when the loop finishes its execution:

• The invariant still holds, since executing the loop means executing the initialization once then the loop body zero or more times.
• And of course the exit condition also holds, since otherwise we would still be looping.

That is how we prove the correctness of a loop: the conjunction of the invariant and the exit condition must yield the property that we seek (in the example, the property, stated above of Result relative to t and x).

We also need to prove that the loop does terminate. This part involves another concept, the loop’s variant, which I will explain in the next section.

For the moment I will not say anything more and let you look at the AutoProof example page (again, you will find it here), run the verification, and read the invariant and other formal elements in the code.

To “run the verification” just click the Verify button on the page. Let me emphasize (and emphasize again and again and again) that clicking Verify will not run the code. There is no execution engine in AutoProof, and the verification does not use any test cases. It processes the text of the program as it appears on the page and below. It applies mathematical techniques to perform the proof; the core property to be proved is that the proposed loop invariant is indeed invariant (i.e. satisfies properties A and B above).

The program being proved on the AutoProof example page is version #6 from the last section, with different variable names. So far for brevity I have used short names such as i, j and m but the program on the AutoProof site applies good naming practices with variables called low, up, middle and the like. So here is that version again with the new variable names:

—  Program attempt #7  (identical to #6 with different variable names) .

from

low := 0 ; up := n

until low ≥ up or Result > 0 loop

middle := low + ((up – low) // 2)

if a [middle] < value then      — The array is now called a rather than t

low := middle + 1

elseif  a [middle] > value then

up := middle

else

Result := middle

end

end

This is exactly the algorithm text on the AutoProof page, the one that you are invited to let AutoProof verify for you. I wrote “algorithm text” rather than “program text” because the actual program text (in Eiffel) includes variant and invariant clauses which do not affect the program’s execution but make the proof possible.

Whether or not these concepts (invariant, variant, program proof) are completely new to you, do try the prover and take a look at the proof-supporting clauses. In the next article I will remove any remaining mystery.

Note and references for section 7

[1] Technically the set of possible [array, value] pairs is finite, but of a size defying human abilities. As I pointed out in the first section, the “model checking” and “abstract interpretation” verification techniques actually attempt to perform an exhaustive test anyway, after drastically reducing the size of the search space. That will be for some other article.

[2]  Jon Bentley: Programming Pearls: Writing Correct Programs, in Communications of the ACM, vol. 26, no. 12, pp. 1040-1045, December 1983, available for example here.

[3] The AutoProof page contains documentations and numerous article references.

8. Understanding the proof

The previous section invited you to run the verification on the AutoProof tutorial page dedicated to the example. AutoProof is an automated proof system for programs. This is just a matter of clicking  “Verify”, but more importantly, you should read the annotations added to the program text, particularly the loop invariant, which make the verification possible. (To avoid any confusion let me emphasize once more that clicking “Verify” does not run the program, and that no test cases are used; the effect is to run the verifier, which attempts to prove the correctness of the program by working solely on the program text.)

Here is the program text again, reverting for brevity to the shorter identifiers (the version on the AutoProof page has more expressive ones):

from

i := 1 ; j := n + 1

until i ≥ j or Result > 0 loop

m := i + (j – i) // 2

if t [m] < x then

i := m + 1

elseif  t [m] > x then

j := m

else

Result := m

end

end

Let us now see what makes the proof possible. The key property is the loop invariant, which reads

A:   1  ≤ i  ≤ j  ≤ n + 1
B:   0  ≤ Result  ≤ n
C:   ∀ k: 1 .. i –1  |  t [k] < x
D:   ∀ k: j .. n  |  t [k] > x
E:    (Result > 0)   ⇒   (t [Result] = x)

The notation is slightly different on the Web page to adapt to the Eiffel language as it existed at the time it was produced; in today’s Eiffel you can write the invariant almost as shown above. Long live Unicode, allowing us to use symbols such as ∀ (obtained not by typing them but by using smart completion, e.g. you start typing “forall” and you can select the ∀ symbol that pops up), ⇒ for  “implies” and many others

Remember that the invariant has to be established by the loop’s initialization and preserved by every iteration. The role of each of its clauses is as follows:

• A: keep the indices in range.
• B: keep the variable Result, whose final value will be returned by the function, in range.
• C and D: eliminate index intervals in which we have determined that the sought value, x, does not appear. Before i, array values are smaller; starting at j, they are greater. So these two intervals, 1..i and j..n, cannot contain the sought value. The overall idea of the algorithm (and most other search algorithms) is to extend one of these two intervals, so as to narrow down the remaining part of 1..n where x may appear.
• E: express that as soon as we find a positive (non-zero) Result, its value is an index in the array (see B) where x does appear.

Why is this invariant useful? The answer is that on exit it gives us what we want from the algorithm. The exit condition, recalled above, is

i ≥ j or Result > 0

Combined with the invariant, it tells us that on exit one of the following will hold:

• Result > 0, but then because of E we know that x appears at position Result.
• i < j, but then A,  C and D  imply that x does not appear anywhere in t. In that case it cannot be true that Result > 0, but then because of B Result must be zero.

What AutoProof proves, mechanically, is that under the function’s precondition (that the array is sorted):

• The initialization ensures the invariant.
• The loop body, assuming that the invariant is satisfied but the exit condition is not, ensures the loop invariant again after it executes.
• The combination of the invariant and the exit condition ensures, as just explained, the postcondition of the function (the property that Result will either be positive and the index of an element equal to x, or zero with the guarantee that x appears nowhere in t).

Such a proof guarantees the correctness of the program if it terminates. We (and AutoProof) must prove separately that it does terminate. The technique is simple: find a “loop variant”, an integer quantity v  which remains non-negative throughout the loop (in other words, the loop invariant includes or implies v ≥ 0) and decreases on each iteration, so that the loop cannot continue executing forever. An obvious variant here is j – i + 1 (where the + 1 is needed because j – i may go down to -1 on the last iteration if x does not appear in the array). It reflects the informal idea of the algorithm: repeatedly decrease an interval i .. j – 1 (initially, 1 .. n) guaranteed to be such that x appears in t if and only if it appears at an index in that interval. At the end, either we already found x or the interval is empty, implying that x does not appear at all.

A great reference on variants and the techniques for proving program termination is a Communications of the ACM article of 2011: [3].

The variant gives an upper bound on the number of iterations that remain at any time. In sequential search, j – i + 1 would be our best bet; but for binary search it is easy to show that  log₂  (j – i + 1) is also a variant, extending the proof of correctness with a proof of performance (the key goal of binary search being to ensure a logarithmic rather than linear execution time).

This example is, I hope, enough to highlight the crucial role of loop invariants and loop variants in reasoning about loops. How did we get the invariant? It looks like I pulled it out of a hat. But in fact if we go the other way round (as advocated in classic books [1] [2]) and develop the invariant and the loop together the process unfolds itself naturally and there is nothing mysterious about the invariant.

Here I cannot resist quoting (thirty years on!) from my own book Introduction to the Theory of Programming Languages [4]. It has a chapter on axiomatic semantics (also known as Hoare logic, the basis for the ideas used in this discussion), which I just made available: see here [5]. Its exercise 9.12 is the starting point for this series of articles. Here is how the book explains how to design the program and the invariant [6]:

In the general case [of search, binary or not] we aim for a loop body of the form

m := ‘‘Some value in 1.. n such that i ≤ m < j’’;

if t [m] ≤ x then

i := m + 1

else

j := m

end

It is essential to get all the details right (and easy to get some wrong):

• The instruction must always decrease the variant j – i, by increasing i or decreasing j. If the the definition of m specified just m ≤ j rather than m < j, the second branch would not meet this goal.
•  This does not transpose directly to i: requiring i < m < j would lead to an impossibility when j – i is equal to 1. So we accept i ≤ m but then we must take m + 1, not m, as the new value of i in the first branch.
•  The conditional’s guards are tests on t [m], so m must always be in the interval 1 . . n. This follows from the clause 0 ≤ i ≤ j ≤ n + 1 which is part of the invariant.
•  If this clause is satisfied, then m ≤ n and m > 0, so the conditional instruction indeed leaves this clause invariant.
• You are invited to check that both branches of the conditional also preserve the rest of the invariant.
• Any policy for choosing m is acceptable if it conforms to the above scheme. Two simple choices are i  and j – 1; they lead to variants of the sequential search algorithm [which the book discussed just before binary search].

For binary search, m will be roughly equal to the average of i and j.

“Roughly” because we need an integer, hence the // (integer division).

In the last section, I will reflect further on the lessons we can draw from this example, and the practical significance of the key concept of invariant.

References and notes for section 8

[1] E.W. Dijkstra: A Discipline of Programming, Prentice Hall, 1976.

[2] David Gries: The Science of Programming, Springer, 1989.

[3] Byron Cook, Andreas  Podelski and Andrey Rybalchenko: Proving program termination, in Communications of the ACM, vol. 54, no. 11, May 2011, pages 88-98, available here.

[4] Bertrand Meyer, Introduction to the Theory of Programming Languages, Prentice Hall, 1990. The book is out of print but can be found used, e.g. on Amazon. See the next entry for an electronic version of two chapters.

[5] Bertrand Meyer Axiomatic semantics, chapter 9 from [3], available here. Note that the PDF was reconstructed from an old text-processing system (troff); the figures could not be recreated and are missing. (One of these days I might have the patience of scanning them from a book copy and adding them. Unless someone wants to help.) I also put online, with the same caveat, chapter 2 on notations and mathematical basis: see here.

[6] Page 383 of [4] and [5]. The text is verbatim except a slight adaptation of the programming notation and a replacement of the variables: i in the book corresponds to i – 1 here, and j to j – 1. As a matter of fact I prefer the original conventions from the book (purely as a matter of taste, since the two are rigorously equivalent), but I changed here to the conventions of the program as it appears in the AutoProof page, with the obvious advantage that you can verify it mechanically. The text extract is otherwise exactly as in the 1990 book.

9. Lessons learned

What was this journey about?

We started with a succession of attempts that might have “felt right” but were in fact all wrong, each in its own way: giving the wrong answer in some cases, crashing (by trying to access an array outside of its index interval) in some cases, looping forever in some cases. Always “in some cases”,  evidencing the limits of testing, which can never guarantee that it exercises all the problem cases. A correct program is one that works in all cases. The final version was correct; you were able to prove its correctness with an online tool and then to understand (I hope) what lies behind that proof.

To show how to prove such correctness properties, I have referred throughout the series to publications from the 1990s (my own Introduction to The Theory of Programming Languages), the 1980s (Jon Bentley’s Programming Pearls columns, Gries’s Science of Programming), and even the 1970s (Dijkstra’s Discipline of Programming). I noted that the essence of my argument appeared in a different form in one of Bentley’s Communications articles. What is the same and what has changed?

The core concepts have been known for a long time and remain applicable: assertion, invariant, variant and a few others, although they are much better understood today thanks to decades of theoretical work to solidify the foundation. Termination also has a more satisfactory theory.

On the practical side, however, the progress has been momentous. Considerable engineering has gone into making sure that the techniques scaled up. At the time of Bentley’s article, binary search was typical of the kind of programs that could be proved correct, and the proof had to proceed manually. Today, we can tackle much bigger programs, and use tools to perform the verification.

Choosing binary search again as an example today has the obvious advantage that everyone can understand all the details, but should not be construed as representative of the state of the art. Today’s proof systems are far more sophisticated. Entire operating systems, for example, have been mechanically (that is to say, through a software tool) proved correct. In the AutoProof case, a major achievement was the proof of correctness [1] of an entire data structure (collections) library, EiffelBase 2. In that case, the challenge was not so much size (about 8,000 source lines of code), but the complexity of both:

• The scope of the verification, involving the full range of mechanisms of a modern object-oriented programming language, with classes,  inheritance (single and multiple), polymorphism, dynamic binding, generics, exception handling etc.
• The code itself, using sophisticated data structures and algorithms, involving in particular advanced pointer manipulations.

In both cases, progress has required advances on both the science and engineering sides. For example, the early work on program verification assumed a bare-bones programming language, with assignments, conditionals, loops, routines, and not much more. But real programs use many other constructs, growing ever richer as programming languages develop. To cover exception handling in AutoProof required both theoretical modeling of this construct (which appeared in [2]) and implementation work.

More generally, scaling up verification capabilities from the small examples of 30 years ago to the sophisticated software that can be verified today required the considerable effort of an entire community. AutoProof, for example, sits at the top of a tool stack relying on the Boogie environment from Microsoft Research, itself relying on the Z3 theorem prover. Many person-decades of work make the result possible.

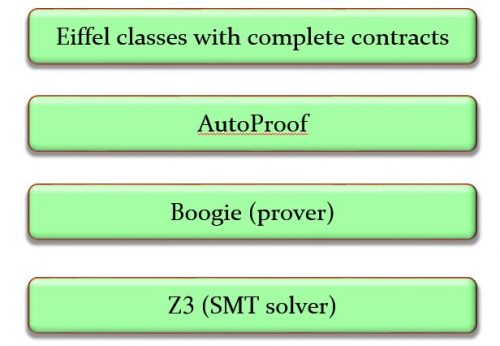
Beyond the tools, the concepts are esssential. One of them, loop invariants, has been illustrated in the final version of our program. I noted in the first article the example of a well-known expert and speaker on testing who found no better way to announce that a video would not be boring than  “relax, we are not going to talk about loop invariants.” Funny perhaps, but unfair. Loop invariants are one of the most beautiful concepts of computer science. Not so surprisingly, because loop invariants are the application to programming of the concept of mathematical induction. According to the great mathematician Henri Poincaré, all of mathematics rests on induction; maybe he exaggerated, maybe not, but who would think of teaching mathematics without explaining induction? Teaching programming without explaining loop invariants is no better.

Below is an illustration (if you will accept my psychedelic diagram) of what a loop is about, as a problem-solving technique. Sometimes we can get the solution directly. Sometimes we identify several steps to the solution; then we use a sequence (A ; B; C). Sometimes we can find two (or more) different ways of solving the problem in different cases; then we use a conditional (if c then A else B end). And sometimes we can only get a solution by getting closer repeatedly, not necessarily knowing in advance how many times we will have to advance towards it; then, we use a loop.

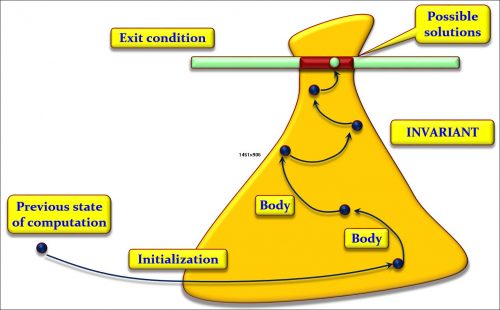
We identify an often large (i.e. very general) area where we know the solution will lie; we call that area the loop invariant. The solution or solutions (there may be more than one) will have to satisfy a certain condition; we call it the exit condition. From wherever we are, we shoot into the invariant region, using an appropriate operation; we call it the initialization. Then we execute as many times as needed (maybe zero if our first shot was lucky) an operation that gets us closer to that goal; we call it the loop body. To guarantee termination, we must have some kind of upper bound of the distance to the goal, decreasing each time discretely; we call it the loop variant.

This explanation is only an illustration, but I hope it makes the ideas intuitive. The key to a loop is its invariant. As the figure suggests, the invariant is always a generalization of the goal. For example, in binary search (and many other search algorithms, such as sequential search), our goal is to find a position where either x appears or, if it does not, we can be sure that it appears nowhere. The invariant says that we have an interval with the same properties (either x appears at a position belonging to that interval or, if it does not, it appears nowhere). It obviously includes the goal as a special case: if the interval has length 1, it defines a single position.

An invariant should be:

1. Strong enough that we can devise an exit condition which in the end, combined with the invariant, gives us the goal we seek (a solution).
2. Weak enough that we can devise an initialization that ensures it (by shooting into the yellow area) easily.
3. Tuned so that we can devise a loop body that, from a state satifying the invariant, gets us to a new one that is closer to the goal.

In the example:

1. The exit condition is simply that the interval’s length is 1. (Technically, that we have computed Result as the single interval element.) Then from the invariant and the exit condition, we get the goal we want.
2. Initialization is easy, since we can just take the initial interval to be the whole index range of the array, which trivially satisfies the invariant.
3. The loop body simply decreases the length of the interval (which can serve as loop variant to ensure termination). How we decrease the length depends on the search strategy; in sequential search, each iteration decreases the length by 1, correct although not fast, and binary search decreases it by about half.

The general scheme always applies. Every loop algorithm is characterized by an invariant. The invariant may be called the DNA of the algorithm.

To demonstrate the relevance of this principle, my colleagues Furia, Velder, and I published a survey paper [6] in ACM Computing Surveys describing the invariants of important algorithms in many areas of computer science, from search algorithms to sorting (all major algorithms), arithmetic (long integer addition, squaring), optimization and dynamic programming  (Knapsack, Levenshtein/Edit distance), computational geometry (rotating calipers), Web (Page Rank)… I find it pleasurable and rewarding to go deeper into the basis of loop algorithms and understand their invariants; like a geologist who does not stop at admiring the mountain, but gets to understand how it came to be.

Such techniques are inevitable if we want to get our programs right, the topic of this article. Even putting aside the Bloch average-computation overflow issue, I started with 5 program attempts, all kind of friendly-looking but wrong in different ways. I could have continued fiddling with the details, following my gut feeling to fix the flaws and running more and more tests. Such an approach can be reasonable in some cases (if you have an algorithm covering a well-known and small set of cases), but will not work for non-trivial algorithms.

Newcomers to the concept of loop invariant sometimes panic: “this is all fine, you gave me the invariants in your examples, how do I find my own invariants for my own loops?” I do not have a magic  recipe (nor does anyone else), but there is no reason to be scared. Once you have understood the concept and examined enough examples (just a few of those in [6] should be enough), writing the invariant at the same time as you are devising a loop will come as a second nature to you.

As the fumbling attempts in the first few sections should show, there is not much of an alternative. Try this approach. If you are reaching these final lines after reading what preceded them, allow me to thank you for your patience, and to hope that this rather long chain of reflections on verification will have brought you some new insights into the fascinating challenge of writing correct programs.

References

[1] Nadia Polikarpova, Julian Tschannen, and Carlo A. Furia: A Fully Verified Container Library, in Proceedings of 20th International Symposium on Formal Methods (FM 15), 2015. (Best paper award.)

[2] Martin Nordio, Cristiano Calcagno, Peter Müller and Bertrand Meyer: A Sound and Complete Program Logic for Eiffel, in Proceedings of TOOLS 2009 (Technology of Object-Oriented Languages and Systems), Zurich, June-July 2009, eds. M. Oriol and B. Meyer, Springer LNBIP 33, June 2009.

[3] Boogie page at MSR, see here for publications and other information.

[4] Z3 was also originally from MSR and has been open-sourced, one can get access to publications and other information from  its Wikipedia page.

[5] Carlo Furia, Bertrand Meyer and Sergey Velder: Loop invariants: Analysis, Classification and Examples, in ACM Computing Surveys, vol. 46, no. 3, February 2014. Available here.

[6] Dynamic programming is a form of recursion removal, turning a recursive algorithm into an iterative one by using techniques known as “memoization” and  “bottom-up computation” (Berry). In this transformation, the invariant plays a key role. I will try to write this up some day as it is a truly elegant and illuminating explanation.

I am giving a “distinguished lecture” at the University of California, Santa Barbara, January 10 (Friday, tomorrow) at 14. The title is A Comprehensive Approach to Requirements Engineering.

The abstract and rest of the information are here.

I will spend the last few minutes of the talk discussing other current developments (verification, concurrency).

Software engineering has improved a lot in the past couple of decades, but there remains an area where the old doomsday style of starting a software engineering paper (software crisis, everything is rotten…) still fits: requirements engineering. Just see the chasm between textbook advice and the practice of most projects.

I have written on requirements in this blog, including very recently, and will continue in forthcoming installments. For today I  want to point to a recent article [1],  presented at the newly revived TOOLS conference in October. It attempts to bring some order and rigor to the basic definitions in the field.

From the abstract:

Requirements engineering is crucial to software development but lacks a precise definition of its fundamental concepts. Even the basic definitions in the literature and in industry standards are often vague and verbose.

To remedy this situation and provide a solid basis for discussions of requirements, this work provides precise definitions of the fundamental requirements concepts and two systematic classifications: a taxonomy of requirement elements (such as components, goals, constraints…) ; and a taxonomy of possible relations between these elements (such as “extends”, “excepts”, “belongs”…).

The discussion evaluates the taxonomies on published requirements documents; readers can test the concepts in two online quizzes.

The intended result of this work is to spur new advances in the study and practice of software requirements by clarifying the fundamental concepts.

This version is a first step; we are aware of its limitations and are already revising the definitions and taxonomy. The project is aimed at providing a solid foundation for a delicate area of software engineering and it will take some time to get it completely right. Still, I think the paper as it is already introduces important concepts. I will within the next two weeks write a more detailed blog article summarizing some of them.

References

[1] Bertrand Meyer, Jean-Michel Bruel, Sophie Ebersold, Florian Galinier, Alexandr Naumchev, The Anatomy of Requirements, in TOOLS 51, Software Technology: Methods and Tools
Innopolis, Russia, October 15–17, 2019, pages 10-40, available here (Springer site, paywall) and here (arXiv draft).

December 16 (next Monday), the newly created Schaffhausen Institute of Technology organizes an entire day of events around three (no less) talks by the physics Nobel prize winner and MIT professor Wolfgang Ketterle.

The culmination of the day is a talk by Prof. Ketterle in the evening on “What happened to the kilogram?”. From the abstract:

For 130 years, a cylinder made of a platinum-iridium alloy stored in Saint-Cloud near Paris was the official definition of a kilogram, the basic unit of mass. This all changed on May 20 of this year: a kilo is now be defined by a fundamental constant of nature known, the Planck constant, which relates the energy of a photon to its frequency: 6.62607015 times 10-34 kilograms times square meters per second. Try that the next time you buy a kilo of asparagus.

Sounds complicated? For MIT’s Wolfgang Ketterle, a Nobel Prize winner, “Conceptually, the definition is very simple”.

Simple? Really? Come to Schaffhausen and hear for yourself whether Prof. Ketterle can make the new kilogram crystal-clear to common mortals.

Earlier in the day, he will give a talk in German on new forms of materials that appear at temperatures near the absolute zero, complete with demonstrations.

More generally, there is a full set of talks throughout the day about various aspects of advanced physics and computer science, and even a “quantum magician”, plus music and food.

Schaffhausen is about 40 minutes from Zurich (or Zurich airport) by train or car.

Attendance is free but registration is recommended. One can register for the full day or for some events only. See further information and registration form here.

The 2020 LASER summer school has been announced. It will take place June 1 to 6* , as always in Elba Island, this year with the theme DevOps, Microservices and Software Development for the Age of the Web. The first five speakers are listed on the conference page, with more to come, from both academia and industry.

This is the 16th edition of the school (already) and, as always, rests on the LASER recipe of “Sea, Sun and Software”: densely packed lectures by top experts with the opportunity to enjoy the extraordinary surroundings of the Island of Elba and the Hotel del Golfo’s unique food, beach and facilities, with lots of time devoted to interactions between speakers and attendees.

This year’s theme is devoted to advances in the newest Web technologies and the corresponding software engineering issues and development models.

*Arrival on May 31st, departure on June 7th.

Earlier this year I was in Sofia for a conference, at the main university (Saint Kliment) which in the entrance hall had an exhibition about its history. There was this student poster and song from I think around 1900:

I like the banner (what do you think?). It even has the correct Latin noun and verb plurals.

Anyone know where to find a university today with that kind of students, that kind of slogan, that kind of attitude and that kind of grammar? Please send me the links.

Recently I had a need to collect my education-related publications, so I went through my publication list and extracted items devoted to issues of learning computer science (informatics) and software engineering. There turned out to be far more than I expected; I did not think of myself as primarily an education researcher but it seems I am that too. (Not so many research computer scientists take the trouble to publish in SIGCSE, ITiCSE and other top CS education venues.)

Without presuming that the list will be of interest I am reproducing it below for the record. All comes from my publication list here, which contains more information, in particular a descriptive paragraph or two for every single publication.

I have also included PhD theses in education. (Whole list of PhD theses supervised here.)

The topics include among others, in approximate chronological order (although the list below is in the reverse order):

• Early experience teaching modern programming concepts in both industry and universities.
• In the nineties, I was full time at Eiffel Software, the development of a general framework for teaching programming. This was written from the safe position of someone in industry advising academic colleagues on what to do (usually the advice goes the other way). I did have, however, the opportunity to practice my preaching in short stints at University of Technology, Sydney and  particularly Monash University. The concept of the Inverted Curriculum (also known as “ Outside-In”) date back to that period, with objects first (actually classes) and contracts first too.
• When I joined ETH, a general paper on the fundamental goals and concepts of software engineering education, “Software Engineering in the Academy”, published in IEEE Computer.
• At ETH, putting the Inverted Curriculum in practice, with 14 consecutive sessions of the introductory programming courses for all computer science students, resulting in the Touch of Class textbook and a number of papers coming out of our observations. An estimated 6000 students took the course. A variant of it has also been given several times at Innopolis University.
• A theory of how to structure knowledge for educational purposes, leading to the notion of “Truc” (Teachable, Reusable Unit of Cognition).
• The development by Michela Pedroni of the Trucstudio environment, similar in its form to an IDE but devoted, instead of the development of programs, to the visual development of courses, textbooks, curricula etc.
• Empirical work by Marie-Hélène Ng Cheong Vee (Nienaltowski) and Michela Pedroni on what beginners understand easily, and not, for example according to the phrasing of compiler error messages.
• Other empirical work, by Michela Pedroni and Manuel Oriol, on the prior knowledge of entering computer science students.
• The DOSE course (Distributed and Outsourced Software Engineering) ran for several years a student project done by joint student teams from several cooperating universities, including Politecnico di Milano which played a key role along with us. It enabled many empirical studies on the effect on software development of having geographically distributed teams. People who played a major role in this effort are, at ETH, Martin Nordio, Julian Tschannen and Christian Estler and, at Politecnico, Elisabetta di Nitto, Giordano Tamburrelli and Carlo Ghezzi.
• Several MOOCs, among the first at ETH, on introductory computing and agile methods. They do not appear below because they are not available at the moment on the EdX site (I do not know why and will try to get them reinstated). The key force there was Marco Piccioni. MOOCs are interesting for many reasons; they are a substitute neither for face-to-face teaching nor for textbooks, but an interesting complement offering novel educational possibilities. Thanks to codeboard, see below, our programming MOOCs provide the opportunity to compile and run program directly from the course exercise pages, compare the run’s result to correct answers for prepared tests, and get immediate feedback .
• A comparative study of teaching effectiveness of two concurrency models, Eiffel SCOOP and JavaThreads (Sebastian Nanz, Michela Pedroni).
• The development of the EiffelMedia multimedia library at ETH, which served as a basis for dozens of student projects over many years. Credit for both the idea and its realization, including student supervision, goes to Till Bay and Michela Pedroni.
• The development (Christian Estler with Martin Nordio) of the Codeboard system and site, an advanced system for cloud support to teach programming, enabling students to compile, correct and run programs on the web, with support for various languages. Codeboard is used in the programming MOOCs.
• A hint system (Paolo Antonucci, Michela Pedroni) to help students get progressive help, as in video games, when they stumble trying to write a program, e.g. with Codeboard.

Supervised PhD theses on education

The following three theses are devoted to educational topics (although many of the  other theses have educational aspects too):

Christian Estler, 2014, Understanding and Improving Collaboration in Distributed Software Development, available here.

Michela Pedroni, 2009, Concepts and Tools for Teaching Programming, available here.

Markus Brändle, 2006: GraphBench: Exploring the Limits of Complexity with Educational Software, available here. (The main supervisor in this case was Jürg Nievergelt.)

MOOCs (Massive Online Open Courses)

Internal MOOCs, and three courses on EdX (links will be added when available):

• Computing: Art, Magic, Science? Part 1 (CAMS 1), 2013.
• Computing: Art, Magic, Science? Part 1 (CAMS 2), 2014.
• Agile Software Development, 2015.

Publications about education

1. Paolo Antonucci, Christian Estler, Durica Nikolic, Marco Piccioni and Bertrand Meyer: An Incremental Hint System For Automated Programming Assignments, in ITiCSE ’15, Proceedings of 2015 ACM Conference on Innovation and Technology in Computer Science Education, 6-8 July 2015, Vilnius, ACM Press, pages 320-325. (The result of a master’s thesis, a system for helping students solve online exercises, through successive hints.) Available here.

2. Jiwon Shin, Andrey Rusakov and Bertrand Meyer: Concurrent Software Engineering and Robotics Education, in 37th International Conference on Software Engineering (ICSE 2015), Florence, May 2015, IEEE Press, pages 370-379. (Describes our innovative Robotics Programming Laboratory course, where students from 3 departments, CS, Mechanical Engineering and Electrical Engineering learned how to program robots.) Available here.

3. Cristina Pereira, Hannes Werthner, Enrico Nardelli and Bertrand Meyer: Informatics Education in Europe: Institutions, Degrees, Students, Positions, Salaries — Key Data 2008-2013, Informatics Europe report, October 2014. (Not a scientific publication but a report. I also collaborated in several other editions of this yearly report series, which I started, from 2011 on. A unique source of information about the state of CS education in Europe.) Available here.

4. (One of the authors of) Informatics education: Europe cannot afford to miss the boat, edited by Walter Gander, joint Informatics Europe and ACM Europe report, April 2013. An influential report which was instrumental in the introduction of computer science in high schools and primary schools in Europe, particularly Switzerland. Emphasized the distinction between “digital literacy” and computer science. Available here.

5. Sebastian Nanz, Faraz Torshizi, Michela Pedroni and Bertrand Meyer: Design of an Empirical Study for Comparing the Usability of Concurrent Programming Languages, in Information and Software Technology Journal Elsevier, volume 55, 2013. (Journal version of conference paper listed next.) Available here.

6. Bertrand Meyer: Knowledgeable beginners, in Communications of the ACM, vol. 55, no. 3, March 2012, pages 10-11. (About a survey of prior knowledge of entering ETH CS students, over many years. Material from tech report below.) Available here.

7. Sebastian Nanz, Faraz Torshizi, Michela Pedroni and Bertrand Meyer: Design of an Empirical Study for Comparing the Usability of Concurrent Programming Languages, in ESEM 2011 (ACM/IEEE International Symposium on Empirical Software Engineering and Measurement), 22-23 September 2011 (best paper award). Reports on a carefully designed empirical study to assess the teachability of various approaches to concurrent programming. Available here.

8. Martin Nordio, H.-Christian Estler, Julian Tschannen, Carlo Ghezzi, Elisabetta Di Nitto and Bertrand Meyer: How do Distribution and Time Zones affect Software Development? A Case Study on Communication, in Proceedings of the 6th International Conference on Global Software Engineering (ICGSE), IEEE Computer Press, 2011, pages 176-184. (A study of the results of our DOSE distributed course, which involved students from different universities in different countries collaborating on a common software development project.) Available here.

9. Martin Nordio, Carlo Ghezzi, Elisabetta Di Nitto, Giordano Tamburrelli, Julian Tschannen, Nazareno Aguirre, Vidya Kulkarni and Bertrand Meyer: Teaching Software Engineering using Globally Distributed Projects: the DOSE course, in Collaborative Teaching of Globally Distributed Software Development – Community Building Workshop (CTGDSD), Hawaii (at ICSE), May 2011. (Part of the experience of our Distributed Outsourced Software Engineering course, taught over many years with colleagues from Politecnico di Milano and elsewhere, see paper in previous entry.) Available here.

10. Bertrand Meyer: From Programming to Software Engineering (slides only), material for education keynote at International Conference on Software Engineering (ICSE 2010), Cape Town, South Africa, May 2010. Available here.

11. Michela Pedroni and Bertrand Meyer: Object-Oriented Modeling of Object-Oriented Concepts, in ISSEP 2010, Fourth International Conference on Informatics in Secondary Schools, Zurich, January 2010, eds. J. Hromkovic, R. Královic, J. Vahrenhold, Lecture Notes in Computer Science 5941, Springer, 2010. Available here.

12. Michela Pedroni, Manuel Oriol and Bertrand Meyer: What Do Beginning CS Majors Know?, ETH Technical Report, 2009. (Unpublished report about the background of 1st-year ETH CS students surveyed over many years. See shorter 2012 CACM version above.) Available here.

13. Bertrand Meyer: Touch of Class: Learning to Program Well Using Object Technology and Design by Contract, Springer, 2009 (also translated into Russian). (Introductory programming textbook, used for many years at ETH Zurich and Innopolis University for the first programming course. The herecontains a long discussion of pedagogical issues of teaching programming and CS.) Book page and text of several chapters here.

14. Michela Pedroni, Manuel Oriol, Lukas Angerer and Bertrand Meyer: Automatic Extraction of Notions from Course Material, in Proceedings of SIGCSE 2008 (39th Technical Symposium on Computer Science Education), Portland (Oregon), 12-15 March 2008, ACM SIGCSE Bulletin, vol. 40, no. 1, ACM Press, 2008, pages 251-255. (As the title indicates, tools for automatic analysis of course material to extract the key pedagogical notions or “Trucs”.) Available here.

15. Marie-Hélène Nienaltowski, Michela Pedroni and Bertrand Meyer: Compiler Error Messages: What Can Help Novices?, in Proceedings of SIGCSE 2008 (39th Technical Symposium on Computer Science Education), Portland (Oregon), Texas, 12-15 March 2008, ACM SIGCSE Bulletin, vol. 40, no. 1, ACM Press, 2008, pages 168-172. (Discusses the results of experiments with different styles of compiler error messages, which can be baffling to beginners, to determine what works best.) Available here.

16. Bertrand Meyer and Marco Piccioni: The Allure and Risks of a Deployable Software Engineering Project: Experiences with Both Local and Distributed Development, in Proceedings of IEEE Conference on Software Engineering & Training (CSEE&T), Charleston (South Carolina), 14-17 April 2008, ed. H. Saiedian, pages 3-16. (Paper associated with a keynote at an SE education conference. See other papers on the DOSE distributed project experience below.) Available here.

17. Till Bay, Michela Pedroni and Bertrand Meyer: By students, for students: a production-quality multimedia library and its application to game-based teaching, in JOT (Journal of Object Technology), vol. 7, no. 1, pages 147-159, January 2008. Available here (PDF) and here (HTML).

18. Marie-Hélène Ng Cheong Vee (Marie-Hélène Nienaltowski), Keith L. Mannock and Bertrand Meyer: Empirical study of novice error paths, Proceedings of workshop on educational data mining at the 8th international conference on intelligent tutoring systems (ITS 2006), 2006, pages 13-20. (An empirical study of the kind of programming mistakes learners make.) Available here.

19. Bertrand Meyer: Testable, Reusable Units of Cognition, in Computer (IEEE), vol. 39, no. 4, April 2006, pages 20-24. (Introduced a general approach for structuring knowledge for teaching purposes: “Trucs”. Served as the basis for some other work listed, in particular papers with Michela Pedroni on the topics of her PhD thesis. Available here.

21. Michela Pedroni and Bertrand Meyer: The Inverted Curriculum in Practice, in Proceedings of SIGCSE 2006, Houston (Texas), 1-5 March 2006, ACM Press, 2006, pages 481-485. (Develops the idea of inverted curriculum which served as the basis for our teaching of programming at ETH, Innopolis etc. and led to the “Touch of Class” textbook.) Available here.

22. Bertrand Meyer: The Outside-In Method of Teaching Introductory Programming, in Perspective of System Informatics, Proceedings of fifth Andrei Ershov Memorial Conference, Akademgorodok, Novosibirsk, 9-12 July 2003, eds. Manfred Broy and Alexandr Zamulin, Lecture Notes in Computer Science 2890, Springer, 2003, pages 66-78. (An early version of the ideas presented in the previous entry.) Available here.

23. Bertrand Meyer: Software Engineering in the Academy, in Computer (IEEE), vol. 34, no. 5, May 2001, pages 28-35. Translations: Russian in Otkrytye Systemy (Open Systems Publications), #07-08-2001, October 2001. (A general discussion of the fundamental concepts to be taught in software engineering. Served as a blueprint for my teaching at ETH.) Available here.

24. Bertrand Meyer: Object-Oriented Software Construction, second edition, Prentice Hall, 1296 pages, January 1997. Translations: Spanish, French Russian, Serbian, Japanese. (Not a publication on education per se but cited here since it is a textbook that has been widely used for teaching and has many comments on pedagogy.)
23. Bertrand Meyer: The Choice for Introductory Software Education, Guest editorial in Journal of Object-Oriented Programming, vol. 7, no. 3, June 1994, page 8. (A discussion of the use of Eiffel for teaching software engineering topics.)

25. Bertrand Meyer, Towards an Object-Oriented Curriculum, in Journal of Object-Oriented Programming, vo. 6, number 2, May 1993, pages 76-81. (Journal version of paper cited next.) Available here.

26. Bertrand Meyer: Towards an Object-Oriented Curriculum, in TOOLS 11, Technology of Object-Oriented Languages and Systems, Santa Barbara, August 1993, eds. Raimund Ege, Madhu Singh and B. Meyer, Prentice Hall 1993, pages 585-594. (Early advocacy for using OO techniques in teaching programming – while I was not in academia. Much of my subsequent educational work relied on those ideas.) Available here.

27. Bertrand Meyer: Object-Oriented Software Construction, Prentice Hall, 592 pages, 1988. (First edition, translated into German, Italian, French, Dutch, Romanian, Chinese. As noted for second edition above, not about education per se, but widely used textbook with pedagogical implications.)

28. Initiation à la programmation en milieu industriel (Teaching Modern Programming Methodology in an Industrial Environment), in RAIRO, série bleue (informatique), vol. 11, no. 1, pages 21-34 1977. (Early paper on teaching advanced programming techniques in industry.) Available here.

29. Claude Kaiser, Bertrand Meyer and Etienne Pichat, L’Enseignement de la Programmation à l’IIE (Teaching Programming at the IIE engineering school), in Zéro-Un Informatique, 1977. (A paper on my first teaching experience barely out of school myself.) Available here.

Some of the folk wisdom going around in software engineering, often cluessly repeated for decades, is just wrong.  It can be particularly damaging when it affects key aspects of software development and is contradicted by solid scientific evidence. The present discussion covers a question that meets both of these conditions: whether it makes sense to add staff to a project to shorten its delivery time.

My aim is to popularize a result that is well known in the software engineering literature, going back to the early work of Barry Boehm [1], and explained with great clarity by Steve McConnell in his 2006 book on software cost estimation [2] under the name “Shortest Possible Schedule”. While an empirical rather than a logical result, I believe it deserves to be called a theorem (McConnell stays shy of using the term) because it is as close as we have in the area of software engineering management to a universal property, confirmed by numerous experimental studies.

This article contributes no new concept since McConnell’s chapter 20 says all there is to say about the topic;  my aim is simply to make the Shortest Possible Schedule Theorem better known, in particular to practitioners.

The myth about shortening project times begins with an observation that is clearly correct, at least in an extreme form. Everyone understands that if our project has been evaluated, through accepted cost estimation techniques, to require three developers over a year we cannot magically hire 36 people to complete it in one month. Productivity does not always scale up.

But neither does common sense. Too often the conclusion from the preceding trival observation takes the form of an old  saw, “Brooks’ Law”: adding people to a late project delays it further. The explanation is that the newcomers cost more through communication overhead than they bring through actual contributions. While a few other sayings of Brooks’ Mythical Man-Month have stood the test of time, this one has always struck me as describing, rather than any actual law, a definition of bad management. Of course if you keep haplessly throwing people at deadlines you are just going to add communication problems and make things worse. But if you are a competent manager expanding the team size is one of the tools at your disposal to improve the state of a project, and it would be foolish to deprive yourself of it. A definitive refutation of the supposed law, also by McConnell, was published 20 years ago [3].

For all the criticism it deserves, Brooks’s pronouncement was at least limited in its scope: it addressed addition of staff to a project that is already late. It is even wronger to apply it to the more general issue of cost-estimating and staffing software projects, at any stage of their progress.  Forty-year-old platitudes have even less weight here. As McConnell’s book shows, cost estimation is no longer a black art. It is not an exact science either, but techniques exist for producing solid estimates.

The Shortest Possible Schedule theorem is one of the most interesting results. Much more interesting than Brooks’s purported law, because it is backed by empirical studies (rather than asking us to believe one person’s pithy pronouncement), and instead of just a general negative view it provides a positive result complemented by a limitation of that result; and both are expressed quantitatively.

Figure 1 gives the general idea of the SPS theorem. General idea only; Figure 2 will provide a more precise view.

Figure 1: General view of the Shortest Possible Schedule theorem.

The  “nominal project” is the result of a cost and schedule estimation yielding the optimum point. The figure and the theorem provide project managers with both a reason to rejoice and a reason to despair:

• Rejoice: by putting in more money, i.e. more people (in software engineering, project costs are essentially people costs [4]), you can bring the code to fruition faster.
• Despair: whatever you do, there is a firm limit to the time you can gain: 25%. It seems to be a kind of universal constant of software engineering.

The “despair” part typically gets the most attention at first, since it sets an absolute value on how much money can buy (so to speak) in software: try as hard as you like, you will never get below 75% of the nominal (optimal) value. The “impossible zone” in Figure 1 expresses the fundamental limitation. This negative result is the reasoned and precise modern replacement for the older folk “law”.

The positive part, however, is just as important. A 75%-empty glass is also 25%-full. It may be disappointing for a project manager to realize that no amount of extra manpower will make it possible to guarantee to higher management more than a 25% reduction in time. But it is just as important to know that such a reduction, not at all insignificant, is in fact reachable given the right funding, the right people, the right tools and the right management skills. The last point is critical: money by itself does not suffice, you need management; Brooks’ law, as noted, is mostly an observation of the effects of bad management.

Figure 1 only carries the essential idea, and is not meant to provide precise numerical values. Figure 2, the original figure from McConnell’s book, is. It plots effort against time rather than the reverse but, more importantly, it shows several curves, each corresponding to a published empirical study or cost model surveyed by the book.

Figure 2: Original illustration of the Shortest Possible Schedule
(figure 2-20 of [3], reproduced with the author’s permission)

On the left of the nominal point, the curves show how, according to each study, increased cost leads to decreased time. They differ on the details: how much the project needs to spend, and which maximal reduction it can achieve. But they all agree on the basic Shortest Possible Schedule result: spending can decrease time, and the maximal reduction will not exceed 25%.

The figure also provides an answer, although a disappointing one, to another question that arises naturally. So far this discussion has assumed that time was the critical resource and that we were prepared to spend more to get a product out sooner. But sometimes it is the other way around: the critical resource is cost, or, concretely, the number of developers. Assume that nominal analysis tells us that the project will take four developers for a year and, correspondingly, cost 600K (choose your currency).  We only have a budget of 400K. Can we spend less by hiring fewer developers, accepting that it will take longer?

On that side, right of the nominal point in Figure 2, McConnell’s survey of surveys shows no consensus. Some studies and models do lead to decreased costs, others suggest that with the increase in time the cost will actually increase too. (Here is my interpretation, based on my experience rather than on any systematic study: you can indeed achieve the original goal with a somewhat smaller team over a longer period; but the effect on the final cost can vary. If the new time is t’= t + T and the new team size s’= s – S, t and s being the nominal values, the cost difference is proportional to  Ts – t’S. It can be positive as well as negative depending on the values of the original t and s and the precise effect of reduced team size on project duration.)

The firm result, however, is the left part of the figure. The Shortest Possible Schedule theorem confirms what good project managers know: you can, within limits, shorten delivery times by bringing all hands on deck. The precise version deserves to be widely known.

References and note

[1] Barry W. Boehm: Software Engineering Economics, Prentice Hall, 1981.

[2] Steve McConnell: Software Estimation ― Demystifying the Black Art, Microsoft Press, 2006.

[3] Steve McConnell: Brooks’ Law Repealed, in IEEE Software, vol. 16, no. 6, pp. 6–8, November-December 1999, available here.

[4] This is the accepted view, even though one might wish that the industry paid more attention to investment in tools in addition to people.

A version of this article was first published on the Comm. ACM blog under the title The Shortest Possible Schedule Theorem: Yes, You Can Throw Money at Software Deadlines

Over the past few days I have come across several people who told me they want to attend the Frontiers In Software Engineering Education (FISEE) workshop in Villebrumier, 11-13 November, but have not registered yet. If that’s your case please register right now because:

• The number of spots is limited (it’s a residential event, everyone is hosted onsite, and there is a set number of rooms).
• We need a preliminary program. The format of the event is flexible, Springer LNCS proceedings come after the meeting, we make room for impromptu presentations and discussions, but still we need a basic framework and we need to finalize it now.

So please go ahead and fill in the registration form.

From the previous posting about FISEE:

The next event at the LASER center in Villebrumier (Toulouse area, Southwest France) is FISEE, Frontiers in Software Engineering Education, see the web site. This small-scale workshop, 11 to 13 November is devoted to what Software Engineering needs, what should be changed, and how new and traditional institutions can adapt to the fast pace of technology.

Workshops at the Villebrumier center favor a friendly, informal and productive interaction between participants, who are all hosted on site. There are no formal submissions, but post-event proceedings will be published as part of the LASER sub-series of Springer Lecture Notes in Computer Science.

Like other events there, FISEE is by invitation; if you are active in the field of software engineering education as an educator, as a potential employer of software engineering graduates, or as a researcher, you can request an invitation by writing to me or one of the other organizers. Attendance is limited to 15-20 participants.

Among already scheduled talks: a keynote by Alexander Tormasov, rector of Innopolis University, and a talk by me on “the 15 concepts of software engineering”.

The next event at the LASER center in Villebrumier (Toulouse area, Southwest France) is FISEE, Frontiers in Software Engineering Education, see the web site. This small-scale workshop, 11 to 13 November is devoted to what Software Engineering needs, what should be changed, and how new and traditional institutions can adapt to the fast pace of technology.

Workshops at the Villebrumier center favor a friendly, informal and productive interaction between participants, who are all hosted on site. There are no formal submissions, but post-event proceedings will be published as part of the LASER sub-series of Springer Lecture Notes in Computer Science.

Like other events there, FISEE is by invitation; if you are active in the field of software engineering education as an educator, as a potential employer of software engineering graduates, or as a researcher, you can request an invitation by writing to me or one of the other organizers. Attendance is limited to 15-20 participants.

Once you have learned the benefits of formally expressing requirements, you keep noticing potential ambiguities and other deficiencies [1] in everyday language. Most such cases are only worth a passing smile, but here’s one that perhaps can serve to illustrate a point with business analysts in your next requirements engineering workshop or with students in your next software engineering lecture.

As a customer of the Swiss telecommunications company Sunrise I receive an occasional “news” email. (As a customer of the Swiss telecommunications company Sunrise I would actually prefer that they spend my money improving  bandwidth,  but let us not digress.) Rather than raw marketing messages these are tips for everyday life, with the presumed intent of ingratiating the populace. For example, today’s message helpfully advises me on how to move house. The admirable advice starts (my translation):

10.7% of all Swiss people relocate every year. Is that your case too for next Autumn?

Actually no, it’s not my case (neither a case of being one of the “Swiss people” nor a case of intending to relocate this Fall). And, ah, the beauty of ridiculously precise statistics! Not 10.8% or 10.6%, mind you, no, 10.7% exactly! But consider the first sentence and think of something similar appearing in a requirements document or user story. Something similar does appear in such documents, all the time, leading to confusions for the programmers interpreting them and to bugs in the resulting systems. Those restless Swiss! Did you know that they include an itchy group, exactly 922,046 people (I will not be out-significant-digited!), who relocate every year?

Do not be silly, I hear you saying. What Sunrise is sharing of its wisdom is that every year a tenth of the Swiss population moves, but not the same tenth every year. Well, OK, maybe I am being silly. But if you think of a programmer reading such a statement about some unfamiliar domain (not one about which we can rely on common sense), the risk of confusion and consequent bugs is serious.

As [1] illustrated in detail, staying within the boundaries of natural language to resolve such possible ambiguities only results in convoluted requirements that make matters worse. The only practical way out is, for delicate system properties, to use precise language, also known technically as “mathematics”.

Here for example a precise formulation of the two possible interpretations removes any doubt. Let Swiss denote the set of Swiss people and  E the number of elements (cardinal) of a finite set E, which we can apply to the example because the set of Swiss people is indeed finite. Let us define slice as the Sunrise-official number of Swiss people relocating yearly, i.e. slice = Swiss ∗ 0.107 (the actual value appeared above). Then one interpretation of the fascinating Sunrise-official fact is:

{s: Swiss | (∀y: Year | s.is_moving (y))} = slice

In words: the cardinal of the set of Swiss people who move every year (i.e., such that for every year y they move during y) is equal to the size of the asserted population subset.

The other possible interpretation, the one we suspect would be officially preferred by the Sunrise powers (any formal-methods fan from Sunrise marketing reading this, please confirm or deny!), is:

∀y: Year | {s: Swiss | s.is_moving (y)} = slice

In words: for any year y, the cardinal of the set of Swiss people who move during y is equal to the size of the asserted subset.

This example is typical of where and why we need mathematics in software requirements. No absolutist stance here, no decree  that everything become formal (mathematical). Natural language is not going into retirement any time soon. But whenever one spots a possible ambiguity or imprecision, the immediate reaction should always be to express the concepts mathematically.

To anyone who has had a successful exposure to formal methods this reaction is automatic. But I keep getting astounded not only by  the total lack of awareness of these simple ideas among the overwhelming majority of software professionals, but also by their absence from the standard curriculum of even top universities. Most students graduate in computer science without ever having heard such a discussion. Where a formal methods course does exist, it is generally as a specialized topic reserved for a small minority, disconnected (as Leslie Lamport has observed [2]) from the standard teaching of programming and software engineering.

In fact all software engineers should possess the ability to go formal when and where needed. That skill is not hard to learn and should be practiced as part of the standard curriculum. Otherwise we keep training the equivalent of electricians rather than electrical engineers, programmers keep making damaging mistakes from misunderstanding ambiguous or inconsistent requirements, and we all keep suffering from buggy programs.

References

[1] Self-citation appropriate here: Bertrand Meyer: On Formalism in Specifications, IEEE Software, vol. 3, no. 1, January 1985, pages 6-25, available here.

[2] Leslie Lamport: The Future of Computing: Logic or Biology, text of a talk given at Christian Albrechts University, Kiel on 11 July 2003, available here.

The DEVOPS 2019 workshop (6-8 May 2019) follows a first 2018 workshop whose proceedings [1] have just been published in the special LASER-Villebrumier subseries of Springer Lecture notes in Computer Science. It is devoted to software engineering aspects of continuous development and new paradigms of software production and deployment, including but not limited to DevOps.

The keynote will be delivered by Gail Murphy, vice-president Research & Innovation at University of British Columbia and one of leaders in the field of empirical software engineering.

The workshop is held at the LASER conference center in Villebrumier near Toulouse. It is by invitation; if you would like to receive an invitation please contact one of the organizers (Jean-Michel Bruel, Manuel Mazzara and me) with a short description of your interest in the field.

Reference

Jean-Michel Bruel, Manuel Mazzara and Bertrand Meyer (eds.), Software Engineering Aspects of Continuous Development and New Paradigms of Software Production and Deployment, First International Workshop, DEVOPS 2018, Chateau de Villebrumier, France, March 5-6, 2018, Revised Selected Papers, see here..