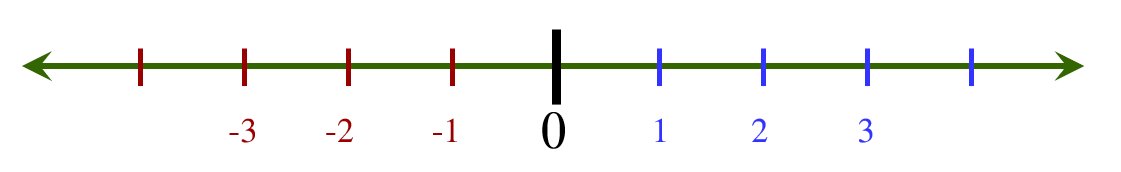Bertrand Meyer's technology+ blog

Reading notes. From: Quelques éléments d’histoire des nombres négatifs (Elements of a history of negative numbers) by Anne Boyé, Proyecto Pénélope, 2002, revision available here; On Solving Equations, Negative Numbers, and Other Absurdities: Part II by Ralph Raimi, available  here; Note sur l’histoire des nombres entiers négatifs (Note on the History of Negative Numbers) by Rémi Lajugie, 2016, here;  The History of Negative Numbers by Leo Rogers, here; Historical Objections against the Number Line, by Albrecht Heeffer, here; Making Sense of Negative Numbers by Cecilia Kilhamn, 2011 PhD thesis at the University of Gothenburg, here.  Also the extensive book by Gert Schubring on Number Concepts Underlying the Development of Analysis in 17-19th Century France and Germany, here. Translations are mine (including from Maclaurin and De Morgan, retranslated from Lajugie’s and Boyé’s French citations). This excursion was spurred by a side remark in the article How to Take Advantage of the Blur Between the Finite and the Infinite by the recently deceased mathematician Pierre Cartier, available here.

At dinner recently, with non-scientists, discussion revolved about ages and a very young child, not even able to read yet, volunteered about his forthcoming little brother that “when he comes out his age will be zero”. An adult remarked “indeed, and right now his age is minus five months”, which everyone young and old seemingly found self-evident. How remarkable!

From a elite concept to grade school topic

It is a characteristic of potent advances in human understanding that for a while they are understandable to a few geniuses only, or, if not geniuses, to a handful of forward-thinking luminaries, and a generation later, sometimes less, they are taught in grade school. When I came across object-oriented programming, those of us who had seen the light, so to speak, were very few. Feeling very much like plotting Carbonari, we would excitedly meet once in a while in exotic locations (for my Simula-fueled band usually in Scandinavia, although for the Smalltalk crowd it must have been California) to share our shared passion and commiserate about the decades it would take for the rest of humankind to see the truth. Then at some point, almost overnight, without any noticeable harbinger, the whole thing exploded and from then on it was object-oriented everything. Nowadays every beginning programmer talks objects — I did not write “understands”, they do not, but that will be for another article.

Zero too was a major invention. Its first recorded use as a number (not just a marker for absent entities) was in India in the first centuries of our era. It is not hard to imagine the mockeries. “Manish here has twenty sheep, Rahul has twelve sheep, and look at that nitwit Shankar, he sold all his sheep and still claims he has some, zero of them he says! Can you believe the absurdity? Ha ha ha.”

That dialog is imaginary, but for another momentous concept, negative numbers, we have written evidence of the resistance. From the best quarters!

The greatest minds on the attack

The great Italian mathematician Cardan (Gerolamo Cardano), in his Ars Magna from 1545, was among the skeptics. As told in a 1758 French History of Mathematics by Montucla (this quote and the next few ones are from Boyé):

In his article 7 Cardan proposes an equation which in our language would be x² + 4 x = 21 and observes that the value of x can equally be +3 or -7, and that by changing the sign of the second term it becomes -3 or +7. The name he gives to such values is “fake”.

The words I am translating here as “fake values” are, in Montucla, valeurs feintes, where feint in French means feigned, or pretended (“pretend values”). Although I have not seen the text of Ars Magna, which is in Latin anyway, I like to think that Cardan was thinking of the Italian word finto. (Used for example  in the title of an opera composed by Mozart at the age of 19, La Finta Giardinera, the fake girl gardener — English has no feminine for “gardener”. The false gardenerette in question is a disguised marchioness.) It is fun to think of negative roots as feigned.

Cardan also uses terms like “abundant” versus “failing” quantities (abondantes and défaillantes in French texts) for positive and negative:

Simple advice: do not confuse failing quantities with abundant quantities. One must add the abundant quantities between themselves, also subtract failing quantities between themselves, and subtract failing quantities from abundant quantities but only by taking species into account, that is to say, only operate same with same […]

There is a recognition of negative values, but with a lot of apprehension. Something strange, the author seems to feel, is at play here. Boyé cites the precedent of Chinese accountants who could manipulate positive values through black sticks and negative ones through red sticks and notes that it resembles what Cardan seems to be thinking here. In the fifteenth century, Nicolas Chuquet “used negative numbers as exponents but referred to them as `absurd numbers’”.

For all his precautions, Cardan did consider negative quantities. No lesser mind as Descartes, a century later (La Géométrie, 1637), is more circumspect. In discussing roots of equations he writes:

Often it turns out that some of those roots are false, or less than nothing [“moindres que rien”] as if one supposes that x can also denote the lack of a quantity, for example 5, in which case we have x + 5 = 0, which, if we multiply it by x³ − 9 x²  + 26 x − 24 = 0 yields  x⁴ − 4 x³ − 19 x² + 106 x − 120 = 0, an equation for which there are four roots, as follows: three true ones, namely 2, 3, 4, and a false one, namely 5.

Note the last value: “5”. Not a -5, but a 5 dismissed as “false”. The list of exorcising adjectives continues to grow: negative values are no longer “failing”, or “fake”, or “absurd”, now for Descartes they are “false”!  To the modern mind they are neither more nor less true than the “true” ones, but to him they are still hot potatoes, to be handled with great suspicion.

Carnot cannot take the heat

One more century later we are actually taking a step back with Lazare Carnot. Not the one of the thermodynamic cycle — that would be his son, as both were remarkable mathematicians and statesmen. Lazare in 1803 cannot hide his fear of negative numbers:

If we really were to obtain a negative quantity by itself, we would have to deduct an effective quantity from zero, that is to say, remove something from nothing : an impossible operation. How then can one conceived a negative quantity by itself?.

(Une quantité négative isolée : an isolated negative quantity, meaning a negative quantity considered in isolation). How indeed! What a scary thought!

The authors of all these statements, even when they consider negative values, cannot bring themselves to talk of negative numbers, only of negative quantities. Numbers, of course, are positive: who has ever heard of a shepherd who is guarding a herd of minus 7 lambs? Negative quantities are a slightly crazy concoction to be used only reluctantly as a kind of kludge.

Lajugie mentions another example, mental arithmetic: to compute 19 x 31  in your head, it is clever to multiply (20 -1) by (30 + 1), but then as you expand the product by applying the laws of distributivity you get negative values.

De Morgan too

We move on by three decades to England and Augustus De Morgan, yes, the one who came up with the two famous laws of logic duality. De Morgan in 1803, as cited by Raimi:

8-3 is easily understood; 3 can be taken from 8 and the remainder is 5; but 3-8 is an impossibility; it requires you to take from 3 more than there is in 3, which is absurd. If such an expression as 3-8 should be the answer to a problem, it would denote either that there was some absurdity inherent in the problem itself, or in the manner of putting it into an equation.

Raimi points out that “De Morgan is not naïve” but wants to caution students about possible errors. Maybe, but we are back to fear and to words such as “absurd”, as used by Chuquet three centuries before. De Morgan (cited by Boyé) doubles down in his reluctance to accept negatives as numbers:

0 − a is just as inconceivable as -a.

Here is an example. A father is 56 years old and his [son] is 29 years old. In how many years will the father’s age be twice his son’s age? Let x be that number of years; x satisfies 56 +x = 2 (29 + x). We find x = -2.

Great, we say, he got it! This simple result is screaming at De Morgan but he has to reject it:

This result is absurd. However if we change x into -x and correspondingly resolve 56−x = 2 (29−x), we find x = -2. The [previous] negative answer shows that we had made an error in the initial phrasing of the equation.

In other words, if you do not like the solution, change the problem! I too can remember a few exam situations in which I would have loved to make an equation more sympathetic by replacing a plus sign with a minus. Too bad no one told me I could.

De Morgan’s comment is remarkable as the “phrasing of  the equation” contained no “error” whatsoever.   The equation correctly reflected the problem as posed. One could find the statement of the problem mischievous (“in how many years” suggests a solution in the future whereas there is only one in the past), but the equation is meaningful and  has a solution — one, however, that horrifies De Morgan. As a result, when discussing the quadratic (second-degree) equation ax² + bx + c = 0, instead of accepting that a, b and c can be negative, he distinguishes no fewer than 6 cases, such as ax² – bx + c = 0, ax² + bx – c = 0 etc. The coefficients are always non-negative, it is the operators that change between + and  -. As a consequence, the determinant actually has two possible values, the one familiar to us, b² – 4ac, but also b² + 4ac for some of the cases. According to Raimi, many American textbooks of the 19th century taught that approach, forcing students to remember all six cases. (For a report about a current teaching distortion of the same topic, see a recent article on the present blog, “Mathematics Is Not a Game of Hit and Miss”, here.)

De Morgan (cited here by Boyé) feels the need to turn this reluctance to use negative numbers into a general rule:

When the answer to a problem is negative, by changing the sign of x in the equation that produced the result, we can discover that an error was made in the method that served to form this equation, or show that the question asked by the problem is too limited.

Sure! It is no longer “if the facts do not fit the theory, change the facts” (a sarcastic definition of bad science), but also “if you do not like the solution, change the problem”. All the more unnecessary (to a modern reader, who thanks to the work of countless mathematicians over centuries learned negative numbers in grade school, and does not spend time wondering whether they mean something) that if we keep the original problem the computed solution, x = -2, makes perfect sense: the father was twice his son’s age two years ago. The past is a negative future. But to see things this way, and to accept that there is nothing fishy here, requires a mindset for which an early 19-th century mathematician was obviously not ready.

And Pascal, and Maclaurin

Not just a mathematician but a great mathematical innovator. What is remarkable in all such statements against negative numbers is that they do not emanate from little minds, unable to grasp abstractions. Quite the contrary! These negative-number-skeptics are outstanding mathematicians. Lajugie gives more examples from the very top. Blaise Pascal in 1670:

Too much truth surprises; I know people who cannot understand that when you deduct 4 from zero, what remains is zero.

(Oh yes?, one is tempted to tell the originator of probability theory, who was fascinated by betting and games of chance: then I put the 4 back and get 4? Quick way to get rich. Give me the address of that casino please.) A friend of Pascal, skeptical about the equality -1 / 1 = 1 / -1: “How could a smaller number be to a larger one as a larger one to a smaller one?”. An English contemporary, John Wallis, one of the creators of infinitesimal calculus — again, not a nitwit! — complains that a / 0 is infinity, but since in a / -1 the denominator is lesser than zero it must follow that a / -1, which is less than zero (since it is negative by the rule of signs), must also be greater than infinity! Nice one actually.

This apparent paradox also bothered the great scientist D’Alembert, the 18-th century co-editor of the Encyclopédie, who resolves it, so to speak, by stating (as cited by Heeffer) that “One can only go from positive to negative through either zero or through infinity”; so unlike Wallis he accepts that 1 / -a is negative, but only because it becomes negative when it passes through infinity. D’Alembert concludes (I am again going after Heeffer) that it is wrong to say that negative numbers are always smaller than zero. Euler was similarly bothered and similarly looking for explanations through infinity: what does Leibniz’s expansion of 1 / (1 – x)  into 1 + x + x² + x³ + … become for x = 2? Well, the sum 1 + 2 + 4 + 8 + … diverges, so 1 / -1 is infinity!

We all know the name “Maclaurin” from the eponymous series. Colin Maclaurin  wrote in 1742, decades after Pascal (Boyé):

The use of the negative sign in algebra leads to several consequences that one initially has trouble accepting and has led to ideas that seem not to have any real foundation.

Again the supposed trouble is the absence of an immediately visible connection to everyday reality (a “real foundation”). And again Maclaurin accepts that quantities can be negative, but numbers cannot:

While abstract quantities can be both negative and positive, concrete quantities are not always capable of being the opposite of each other.

(cited by Kilhamn). Apparently Colin’s wife Anne never thought of buying him a Réaumur thermometer (see below) for his birthday.

Yes, two negatives make a positive

We may note that the authors cited above, and many of their contemporaries, had no issue manipulating negative quantities in some contexts, and to accept the law of signs, brilliantly expressed by the Indian mathematician Brahmagupta  in the early 7th century (not a typo); as cited by Rogers:

A debt minus zero is a debt.

A fortune minus zero is a fortune.

Zero minus zero is a zero.

A debt subtracted from zero is a fortune.

A fortune subtracted from zero is a debt.

The product of zero multiplied by a debt or fortune is zero.

The product of zero multiplied by zero is zero.

The product or quotient of two fortunes is one fortune.

The product or quotient of two debts is one fortune.

The product or quotient of a debt and a fortune is a debt.

The product or quotient of a fortune and a debt is a debt.

That view must have been clear to accountants. Whatever Pascal may have thought, 4 francs removed from nothing do not vanish; they become a debt. What the great mathematicians cited above could not fathom was that there is such a thing as a negative number. You can count up as far as your patience will let you; you can then count down, but you will inevitably stop. Everyone knows that, and even Pascal or Euler have trouble going beyond. (Old mathematical joke: “Do you know about the mathematician who was afraid of negative numbers? He will stop at nothing to avoid them”.)

The conceptual jump that took centuries to achieve was to accept that there are not only negative quantities, but negative numbers: numbers in their own right, not just temporarily  negated positive numbers (that is, the only ones to which we commonly rely in everyday life), prefaced with a minus sign because we want to use them as “debts”, but with the firm intention to move them back to the other side so as to restore their positivity  — their supposed naturalness —  at the end of the computation. We have seen superior minds “stopping at nothing” to avoid that step.

Others were bolder; Schubring has a long presentation of how Fontenelle, an 18-th century French scientist and philosopher who contributed to many fields of knowledge,  made the leap.

Not everyone may yet get it

While I implied above that today even small children understand the concept, we may note in passing that there may still be people for whom it remains a challenge. Lajugie notes that the Fahrenheit temperature scale frees people from having to think about negative temperatures in ordinary circumstances, but since the 18-th century the (much more reasonable) Réaumur thermometer and Celsius scale goes under as well as above zero, helping people get familiar with negative values as something quite normal and not scary. (Will the US ever switch?)

Maybe the battle is not entirely won.  Thanks to Rogers I learned about the 2018 Lottery Incident in the United Kingdom of Great Britain and Northern Ireland, where players could win by scratching away, on a card, a temperature lower than the displayed figure. Some temperatures were below freezing. The game had to be pulled after less than a week as a result of player confusion. Example complaints included this one from a  23-year-old who was adamant she should have won:

“On one of my cards it said I had to find temperatures lower than -8. The numbers I uncovered were -6 and -7 so I thought I had won, and so did the woman in the shop. But when she scanned the card the machine said I hadn’t. I phoned Camelot [the lottery office] and they fobbed me off with some story that -6 is higher – not lower – than -8 but I’m not having it. I think Camelot are giving people the wrong impression – the card doesn’t say to look for a colder or warmer temperature, it says to look for a higher or lower number. Six is a lower number than 8. Imagine how many people have been misled.“

Again, quantities versus numbers. As we have seen, she could claim solid precedent for this reasoning. Most people, of course, have figured out that while 8 is greater than 6 (actually, because of that), -6 is greater than -8. But as Lajugie points out the modern, rigorous definition of negative numbers is (in the standard approach) far from the physical intuition (which typically looks like the two-directional line pictured at the beginning of this article, with numbers spreading away from zero towards both the right and the left). The picture helps, but it is only a picture.

Away from the perceptible world

If we ignore the intuition coming from observing a Réaumur or Celsius thermometer (which does provide a “real world” guide), the early deniers of negative numbers were right that this concept does not directly reflect the experiential understanding of numbers, readily accessible to everyone. The general progress of science, however, has involved moving away from such immediate intuition. Everyday adventures (such as falling on the floor) absolutely do not suggest to us that matter is made of sparse atoms interacting through electrical and magnetic phenomena. This march towards abstraction has guided the evolution of modern science — most strikingly, the evolution of modern mathematics.

Some lament this trend; think of the negative reactions to the so-called “new math”. (Not from me. I was caught by the  breaking of the wave and loved every minute of it.) But there is no going back; in addition, it is well known that some of the initially most abstract mathematical development, initially pursued without any perceived connection with reality, found momentous unexpected applications later on; two famous examples are Minkowski’s space-time formalism, which provided the mathematical framework for specifying relativity, and number-theoretical research about factoring large numbers into primes, which made modern cryptography (and hence e-commerce) possible.

Negative numbers too required abstraction to acquire mathematical activity. That step required setting aside the appeal to intuition and considering the purely concepts solely through its posited properties. We computer scientists would say “applying the abstract data type approach”. The switch took place sometime in the middle of the 19th century, spurred among others by Évariste Galois. The German mathematician Hermann Hankel — who lived only a little longer than Galois — explained clearly how this transition occurred for negative numbers (cited by Boyé among others):

The [concept of] number is no longer today a thing, a substance that is supposed to exist outside of the thinking subject or the objects that lead to it being considered; it is no longer an independent principle, as the Pythagoreans thought. […] The mathematician considers as impossible only that which is logically impossible, in the sense of implying a contradiction. […] But if the numbers under study are logically possible, if the underlying concept is defined clearly and distinctly, the question can no longer be whether a substrate exists in the world of reality.

A very modern view: if you can dream it, and you can make it free of contradiction (well, Hankel lived in the blissful times before Gödel), then you can consider it exists. An engineer might replace the second of these conditions by: if you can build it. And a software engineer, by: if you can compile and run it. In the end it is all the same idea.

Formally: a general integer is an equivalence class

In modern mathematics, while no one forbids you from clinging for help to some concrete intuition such as the Celsius scale, it is not part of the definition. Negative numbers are formally defined members of the zoo.

For those interested (and not remembering the details), the rigorous definition goes like this. We start from zero-or-positive integers (the set N of “natural” numbers) and consider pairs [a, b] of numbers (as we would do to define rationals, but the sequel quickly diverges). We define an equivalence relation which holds with another pair [a’, b’] if a + b’ = a’ + b. Then we can define the set Z of all integers (positive, zero, negative) as the quotient of N x N by that relation. The intuition if that the characteristic property of an equivalence class, such as [1, 4], [2, 5],  [3, 6]… , is that b – a, the difference between the second and first values, is the same for all pairs: 3 in this example (4 – 1, 5 – 2, 6 – 3 etc.). At least that property holds for b >= a; since we are starting from N, subtraction is defined only in that case. But then if we take that quotient as the definition of Z, we call members of that set “negative”, by pure convention, whenever b < a (if this property holds for one of the pairs in an equivalence class it holds for all of them), and positive if b > a. Zero is obtained for a = b.

We reestablish the connection with our good old natural integers by identifying N with the subset of Z for which b >= a. (This is an informal statement; the correct technical phrasing is that there is a “bijection” — a one-to-one correspondence, in fact an isomorphism — between that subset and N.) So we have plunged, or “embedded”, N into something bigger, to which most of its treasured properties (associativity and commutativity of addition etc.) immediately spread, while some limitations disappear; in particular, unlike in N, we can now subtract any Z integer from any other.

We also get the opposites of numbers as a result: for any m in Z, we can easily prove that there is another one n such that m + n = 0. That n can be written -m. The property is true for both positive and negative numbers, concepts that are also easy to define: we show that “>” is one of those operations that extend from N to Z, and the positive numbers are those m such that m > 0. Then if m is positive -m is negative, and conversely; 0 is the only number for which m = -m.

Remarkably, Z too is in one-to-one correspondence with N. (It is one of the definitions of an infinite set that it can be in one-to-one correspondence with one of its strict subsets, something that is obviously not possible for a finite set. To shine in cocktail parties you can refer to this property as “Dedekind-infinite”.) In other words, we have uncovered yet a new attraction of Hilbert’s Grand Hotel: the hotel has an annex, ready for the case of a guest coming with an unannounced companion. The companion will be hosted in the annex, in a room uniquely paired with the original guest’s room. The annex is a second hotel, but it is not exactly like the first: it does not have an annex of its own in the form of yet another hotel. It does have an annex, but that is the original hotel (the hotel of which it itself is the annex).

If you were not aware of the construction through equivalence classes of pairs and your reaction is “so much ado about so little! I do not need any of this to understand negative numbers and to know that m + -m = 0”, well, maybe, but you are missing part of the story: the observation that even the “natural” numbers are not that natural. Those we can readily apprehend as part of “natural” reality are the ones from 1 to something like 1000,  denoting quantities that we can reasonably count. If you really have extraordinary patience and time make this 1000,000 or even 1 million, that does not change the argument.

Even zero, as noted, took millennia to be recognized as a number. Beyond the numbers that we can readily fathom in relation to our experience at human scale, the set of natural integers is also an intellectual fiction. (Its official construction in the modern mathematical canon is seemingly even more contorted than the extension to Z sketched above: N, in the so-called Zermelo-Fraenkel theory (more pickup lines for cocktail parties!) contains the empty set for 0, and then sets each containing the previous one and a set made of that previous one. It is clearer with symbols: ø, {ø}, {ø, {ø}}, {ø, {ø}, {ø, {ø}}}, ….)

Coming back to negative numbers, Riemann (1861, cited by Schubring) held their construction as a fundamental step in the generalization process that characterizes mathematics, beautifully explaining the process:

The original object of mathematics is the integer number; the field of study increases only gradually. This extension does not happen arbitrarily, however; it is always motivated by the fact that the initially restricted view leads toward a need for such an extension. Thus the task of subtraction requires us to seek such quantities, or to extend our concept of quantity in such a way that its execution is always possible, thus guiding us to the concept of the negative.

Nature and nurture

The generalization process is also a process of abstraction. The move away from the “natural” and “intuitive” is inevitable to understand negative numbers. All the misunderstandings and fears by great minds, reviewed above, were precisely caused by an exaggerated, desperate attempt to cling to supposedly natural concepts. And we only talked about negative numbers! Similar or worse resistance met the introduction of imaginary and complex numbers (the names themselves reflect the trepidation!), quaternions and other fruitful but artificial creation of mathematics. Millenia before, the Greeks experienced shock when they realized that numbers such as π and the square root of 2 could not be expressed as ratios of integers.

Innovation occurs when someone sets out to disprove a statement of impossibility. (This technique also lies behind one approach to solving puzzles and riddles: you despair that there is no way out; then try to prove that there is no solution. Failing to complete that proof might end up opening for you the path to one.)

Parallels exist between innovators and children. Children do not know yet that some things are impossible; they make up ways. Right now I am sitting next to the Rhine and I would gladly take a short walk on the other bank, but I do not want to go all the way to the bridge and back. If I were 4 years old, I would dream up some magic carpet or other fancy device, inferred from bedtime stories, that would instantly transport me there. We grow up and learn that there are no magic carpets, but true innovators who see an unsolved problem refuse to accept that state of affairs.

In their games, children often use the conditional: “I would be a princess, and you would be a magician!”. Innovators do this too when they refuse to be stopped by conventional-wisdom statements of impossibility. They set out to disprove the statements. The French expression “prouver le mouvement en marchant”, prove movement by walking, refers to the Greek philosophers Diogenes of Sinope and  Zeno of Elea. Zeno, the story goes, used the paradox of Achilles and the tortoise to claim he had proved that movement is impossible. Diogenes proved the reverse by starting to walk.

In mathematics and in computer science, we are even more like children because we can in fact summon our magic carpets — build anything we dream of, provided we can define it properly. Mathematics and computer science are among the best illustrations of Yuval Noah Harari’s thesis that a defining characteristic of the human race is our ability to tell ourselves stories, including very large and complex stories. A mathematical theory is a story that we tell ourselves and to which we can convert other mathematicians (plus, if the theory is really successful, generations of future students). Computer programs are the same with the somewhat lateral extra condition that we must also enable some computing system to execute it, although that system is itself a powerful story that has undergone the same process. You can find variants of these observations in such famous pronouncements as Butler Lampson’s “in computer science, we can solve any problem by introducing an extra level of indirection” and Alan Kay‘s  “the best way to predict the future is to invent it”.

There is a difference, however, with children’s role-playing; and it can have dramatic effects. Children can indulge in make-believe for quite some time, continuing to live their illusions until they grow up and become reasonable. Normally they will not experience bad consequences (well, apart from the child who believes a little too hard, or from a window little too high, that his arms really are wings.) In adult innovation, sooner or later you have to reconcile the products of your imagination with the world. It may be the physical world (your autonomous robot was fantastic in the lab but it requires heavy batteries making it impractical), but things are just as bad with the virtual world of mathematics or software. It is great to define and extend your own freaky artificial worlds, but at some point you have to make sure they are consistent not just with already defined worlds but with themselves. As noted earlier, a mathematical concoction, however audacious, should be free of contradictions; and a software concept, however powerful, should be implementable. (Efficiently implementable.)

By any measure the most breathtaking virtual construction of modern mathematics is Cantor’s set theory, which scared many mathematicians,  the way negative numbers had terrified their predecessors. (Case in point: the editor of a journal to which Cantor had submitted a paper wrote that it was “a hundred years too soon”.  Cantor did not want to wait until 1984. The great mathematician Kronecker described him as “a corrupter of youth”. And so on.) More enlightened colleagues, however, soon recognized the work as ushering in a new era. Hilbert, in particular, was a great supporter, as were many of the top names in several countries. Then intellectual disaster struck.

Cantor himself and others, most famously Russell in a remark included in a letter of Frege, noticed a problem. If sets can contain other sets, and even contain themselves (the set of infinite sets must be infinite), what do we make of the set of all sets that do not contain themselves? Variants of this simple question so shook the mathematical edifice that it took a half-century to put things back in order.

Dream, check, build

Cantor, for his part, went into depression and illness. He died destitute and desperate. There may not have been a direct cause-to-effect relationship, but certainly the intellectual rejection and crisis did not help.

All the sadder that in the end set theory, after significant cleanup, turned out to be one of the biggest successes of history. We still discuss the paradoxes, but it is unlikely that today they prevent anyone from sleeping soundly at night.

Unlike those genuinely disturbing paradoxes of set theory, the paradoxes that led mathematicians of previous centuries to reject negative numbers were apparent only. They were not paradoxes but tokens of intellectual timidity.

The sole reason for fearing and skirting negative numbers was an inability to accept a construction that contradicted a simplistic view of physical reality. Like object-oriented programming and many other bold advances, all that was required was the audacity to take imagined abstractions seriously.

Dream it; check it; build it.

July 14 (still here for 15 minutes) is not a bad opportunity to announced the publication of a new book: The French School of Programming.

The book is a collection of chapters, thirteen of them, by rock stars of programming and software engineering research (plus me), preceded by a Foreword by Jim Woodcock and a Preface by me. The chapters are all by a single author, reflecting the importance that the authors attached to the project. Split into four sections after chapter 1, the chapters are, in order:

1. The French School of Programming: A Personal View, by Gérard Berry (serving as a general presentation of the subsequent chapters).

Part I: Software Engineering

2. “Testing Can Be Formal Too”: 30 Years Later, by  Marie-Claude Gaudel

3. A Short Visit to Distributed Computing Where Simplicity Is Considered a First-Class Property, by Michel Raynal

4. Modeling: From CASE Tools to SLE and Machine Learning, by Jean-Marc Jézéquel

5. At the Confluence of Software Engineering and Human-Computer Interaction: A Personal Account,  by Joëlle Coutaz

Part II:  Programming Language Mechanisms and Type Systems

6. From Procedures, Objects, Actors, Components, Services, to Agents, by  Jean-Pierre Briot

7. Semantics and Syntax, Between Computer Science and Mathematics, by Pierre-Louis Curien

8. Some Remarks About Dependent Type Theory, by Thierry Coquand

Part III: Theory

9. A Personal Historical Perspective on Abstract Interpretation, by Patrick Cousot

10. Tracking Redexes in the Lambda Calculus, by  Jean-Jacques Lévy

11. Confluence of Terminating Rewriting Computations, by  Jean-Pierre Jouannaud

Part IV: Language Design and Programming Methodology

12. Programming with Union, Intersection, and Negation Types, by Giuseppe Castagna

13, Right and Wrong: Ten Choices in Language Design, by Bertrand Meyer

What is the “French School of Programming”? As discussed in the Preface (although Jim Woodcock’s Foreword does not entirely agree) it is not anything defined in a formal sense, as the variety of approaches covered in the book amply demonstrates. What could be more different (for example) than Coq, OCaml (extensively referenced by several chapters) and Eiffel? Beyond the differences, however, there is a certain je ne sais quoi of commonality; to some extent, in fact, je sais quoi: reliance on mathematical principles, a constant quest for simplicity, a taste for elegance. It will be for the readers to judge.

Being single authors of their chapters, the authors felt free to share some of their deepest insights an thoughts. See for example Thierry Coquand’s discussion of the concepts that led to the widely successful Coq proof system, Marie-Claude Gaudel’s new look at her seminal testing work of 30 years ago, and Patrick Cousot’s detailed recounting of the intellectual path that led him and Radhia to invent abstract interpretation.

The French School of Programming
Edited by Bertrand Meyer
Springer, 2024. xxiv + 439 pages

Book page on Springer site
Amazon US page
Amazon France page
Amazon Germany page

The book is expensive (I tried hard to do something about it, and failed). But many readers should be able to download it, or individual chapters, for free through their institutions.

It was a privilege for me to take this project to completion and work with such extraordinary authors who produced such a collection of gems.

I harbor no illusion about the effectiveness of airing this particular pet peeve; complaining about it has about the same chance of success as protesting against split infinitives or music in restaurants. Still, it is worth mentioning that the widespread use of the word “statement” to denote a programming language element, such as an assignment, that directs a computer to perform some change, is misleading. “Instruction” is the better term.

A “statement” is “something stated, such as a single declaration or remark, or a report of fact or opinions” (Merriam-Webster).

Why does it matter? The use of “statement” to mean “instruction” obscures a fundamental distinction of software engineering: the duality between specification and implementation. Programming produces a solution to a problem; success requires expressing both the problem, in the form of a specification, and the devised solution, in the form of an implementation. It is important at every stage to know exactly where we stand: on the problem side (the “what”) or the solution side (the “how”). In his famous Goto Statement Considered Harmful of 1968, Dijkstra beautifully characterized this distinction as the central issue of programming:

Our intellectual powers are rather geared to master static relations and our powers to visualize processes evolving in time are relatively poorly developed. For that reason we should do (as wise programmers aware of our limitations) our utmost to shorten the conceptual gap between the static program and the dynamic process, to make the correspondence between the program (spread out in text space) and the process (spread out in time) as trivial as possible.

Software verification, whether conducted through dynamic means (testing) or static techniques (static analysis, proofs of correctness), relies on having separately expressed both a specification of the intent and a proposed implementation intended to realize that intent. They have to remain distinct; otherwise we cannot even define what it means that the program should be correct (correct with respect to what?), and even less what it means to validate the program (validate it against what?).

In many approaches to verification, the properties against which we validate programs are called assertions. An assertion expresses a property that should hold at some point of program execution. For example, after the assignment instruction a := b + 1, the assertion a ≠ b will hold. This notion of assertion is used both in testing frameworks, such as JUnit for Java or PyUnit for Python, and in program proving frameworks; see, for example, the interactive Web-based version of the AutoProof program-proving framework for Eiffel at autoproof.sit.org, and of course the entire literature on axiomatic (Floyd-Hoare-Dijkstra-style) verification.

The difference between the instruction and the assertion is critical: a := b + 1 tells the computer to do something (change the value of a), as emphasized here by the “:=” notation for assignment; a ≠ b does not direct the computer or the computation to do anything, but simply states a property that should hold at a certain stage of the computation if everything went fine so far.

In the second case, the word “states” is indeed appropriate: an assertion states a certain property. The expression of that property, a ≠ b, is a “statement” in the ordinary English sense of the term. The command to the computer, a := b + 1, is an instruction whose effect is to ensure the satisfaction of the statement a ≠ b. So if we use the word “statement” at all, we should use it to mean an assertion, not an instruction.

If we start calling instructions “statements” (a usage that Merriam-Webster grudgingly accepts in its last entry for the term, although it takes care to define it as “an instruction in a computer program,” emphasis added), we lose this key distinction.

There is no reason for this usage, however, since the word “instruction” is available, and entirely appropriate.

So, please stop saying “an assignment statement” or “a print statement“; say “an assignment instruction” and so on.

Maybe you won’t, but at least you have been warned.

This article was first published in the “Communications of the ACM” blog.

Li Huang (PhD student at SIT) will be presenting at an ISSRE workshop the paper Improving Counterexample Quality from Failed Program Verification, written with Manuel Oriol and me. One can find the text on arXiv here. (I will update this reference with the official publication link when I have it.)

The result being presented is part of a more general effort at combining proofs and tests (with other papers in the pipeline). The idea of treating proofs and tests as complementary rather than competing methods of software verification is an old pursuit of mine (which among other consequences resulted in the creation with Yuri Gurevich of the Tests and Proofs conference, which I see is continuing to run). A particular observation is that failure means a different thing for proofs and tests.

A failed test provides interesting information (in fact it is a successful proof — of incorrectness). A successful proof is, of course, also interesting (in principle it should be end of the story), whereas a successful test tells us very little. But in the practice of program proving the common occurrence is failure to prove a program element correct. You are typically left with no clue as to the source of the failure. In the AutoProof verification system for Eiffel, we are able to rely on the underlying technology (Boogie and Z3) to extract a counterexample which gives concrete evidence: as with a failed test, a programmer can in general quickly understand what is wrong.

In other words, the useless negative result of the bottom-left entry of the above picture can produce a useful result:

The general approach is the subject of another article but this one focuses on producing tests that are actually significant for the programmer. If you get very large values, you will not immediately be able to relate to them. Hence the need for a process of minimization, described in the article. The results on our examples are encouraging, making it possible to evidence the bug on very small integer values.

Reference

Li Huang, Bertrand Meyer and Manuel Oriol: Improving Counterexample Quality from Failed Program Verification, 6th International Workshop on Software Faults, October 2022. Preprint available on arXiv here. The program workshop is available here; the presentation is on Monday, 31 October, 15:55 CET (7:55 AM Los Angeles, 10:55 New York).

I am happy to announce the publication of the Handbook of Requirements and Business Analysis (Springer, 2022).

It is the result of many years of thinking about requirements and how to do them right, taking advantage of modern principles of software engineering. While programming, languages, design techniques, process models and other software engineering disciplines have progressed considerably, requirements engineering remains the sick cousin. With this book I am trying to help close the gap.

The Handbook introduces a comprehensive view of requirements including four elements or PEGS: Project, Environment, Goals and System. One of its principal contributions is the definition of a standard plan for requirements documents, consisting of the four corresponding books and replacing the obsolete IEEE 1998 structure.

The text covers both classical requirements techniques and novel topics such as object-oriented requirements and the use of formal methods.

The successive chapters address: fundamental concepts and definitions; requirements principles; the Standard Plan for requirements; how to write good requirements; how to gather requirements; scenario techniques (use cases, user stories); object-oriented requirements; how to take advantage of formal methods; abstract data types; and the place of requirements in the software lifecycle.

The Handbook is suitable both as a practical guide for industry and as a textbook, with over 50 exercises and supplementary material available from the book’s site.

You can find here a book page with the preface and sample chapters.

To purchase the book, see the book page at Springer and the book page at Amazon US.

Short version: the full text of my Introduction to the Theory of Programming Languages book (second printing, 1991) is now available. This page has more details including the table of chapters, and a link to the PDF (3.3MB, 448 + xvi pages).

The book is a survey of methods for language description, particularly semantics (operational, translational, denotational, axiomatic, complementary) and also serves as an introduction to formal methods. Obviously it would be written differently today but it may still have its use.

A few days ago I released the Axiomatic Semantics chapter of the book, and the chapter introducing mathematical notations. It looked at the time that I could not easily  release the rest in a clean form, because it is impossible or very hard to use the original text-processing tools (troff and such). I could do it for these two chapters because I had converted them years ago for my software verification classes at ETH.

By perusing old files, however,  I realized that around the same time (early 2000s) I actually been able to produce PDF versions of the other chapters as well, even integrating corrections to errata  reported after publication. (How I managed to do it then I have no idea, but the result looks identical, save the corrections, to the printed version.)

The figures were missing from that reconstructed version (I think they had been produced with Brian Kernighan’s PIC graphical description language , which is even more forgotten today than troff), but I scanned them from a printed copy and reinserted them into the PDFs.

Some elements were missing from my earlier resurrection: front matter, preface, bibliography, index. I was able to reconstruct them from the original troff source using plain MS Word. The downside is that they are not hyperlinked; the index has the page numbers (which may be off by 1 or 2 in some cases because of reformatting) but not hyperlinks to the corresponding occurrences as we would expect for a new book. Also, I was not able to reconstruct the table of contents; there is only a chapter-level table of contents which, however, is hyperlinked (in other words, chapter titles link to the actual chapters). In the meantime I obtained the permission of the original publisher (Prentice Hall, now Pearson Education Inc.).

Here again is the page with the book’s description and the link to the PDF:

bertrandmeyer.com/ITPL

I have released for general usage the chapter on axiomatic semantics of my book Introduction to the Theory of Programming Languages. It’s old but I think it is still a good introduction to the topic. It explains:

• The notion of theory (with a nice — I think — example borrowed from an article by Luca Cardelli: axiomatizing types in lambda calculus).
• How to axiomatize a programming language.
• The notion of assertion.
• Hoare-style pre-post semantics, dealing with arrays, loop invariants etc.
• Dijkstra’s calculus of weakest preconditions.
• Non-determinism.
• Dealing with routines and recursion.
• Assertion-guided program construction (in other words, correctness by construction), design heuristics (from material in an early paper at IFIP).
• 26 exercises.

The text can be found at

https://se.inf.ethz.ch/~meyer/publications/theory/09-axiom.pdf

It remains copyrighted but can be used freely. It was available before since I used it for courses on software verification but the link from my publication page was broken. Also, the figures were missing; I added them back.

I thought I only had the original (troff) files, which I have no easy way to process today, but just found PDFs for all the chapters, likely produced a few years ago when I was still able to put together a working troff setup. They are missing the figures, which I have to scan from a printed copy and reinsert. I just did it for the chapter on mathematical notations, chapter 2, which you can find at https://se.inf.ethz.ch/~meyer/publications/theory/02-math.pdf. If there is interest I will release all chapters (with corrections of errata reported by various readers over the years).

The chapters of the book are:

• (Preface)

1. Basic concepts
2. Mathematical background (available through the link above).
3. Syntax (introduces formal techniques for describing syntax, included a simplified BNF).
4. Semantics: the main approaches (overview of the techniques described in detail in the following chapters).
5. Lambda calculus.
6. Denotational semantics: fundamentals.
7. Denotational semantics: language features (covers denotational-style specifications of records, arrays, input/output etc.).
8. The mathematics of recursion (talks in particular about iterative methods and fixpoints, and the bottom-up interpretation of recursion, based on work by Gérard Berry).
9. Axiomatic semantics (available through the link above).
10. Complementary semantic definitions (establishing a clear relationship between different specifications, particular axiomatic and denotational).

• Bibliography

Numerous exercises are included. The formal models use throughout a small example language called Graal (for “Great Relief After Ada Lessons”).  The emphasis is on understanding programming and programming languages through simple mathematical models.

My book Object-Oriented Software Construction, 2nd edition (see the Wikipedia page) has become hard to get. There are various copies floating around the Web but they often use bad typography (wrong colors) and are unauthorized.

In response to numerous requests and in anticipation of the third edition I have been able to make it available electronically (with the explicit permission of the original publisher).

You can find the link on another page on this site. (In sharing or linking please use that page, not the URL of the actual PDF which might change.)

I hope having the text freely available proves useful.

The Chair of Software Engineering, my group at the Schaffhausen Institute of Technology in Switzerland (SIT), has open positions for both PhD students and postdocs. We are looking for candidates with a passion for reliable software and a mix of theoretical knowledge and practical experience in software engineering. Candidates should have degrees in computer science or related fields: a doctorate for postdoc positions, a master’s degree for PhD positions. Postdoc candidates should have a substantial publication record. Experience is expected in one or more of the following fields:

• Software verification (axiomatic, model-checking, abstract interpretation etc.).
• Advanced techniques of software testing.
• Formal methods, semantics of programming languages.
• Concurrent programming.
• Design by Contract, Eiffel, techniques of correctness-by-construction.

Some of the work involves the AutoProof framework, under development at SIT (earlier at ETH), although other topics are also available, particularly in static analysis.

Compensation is attractive. Candidates must have the credentials to work in Switzerland (typically, citizenship or residence in Switzerland or the EU). Although we work in part remotely like everyone else these days, the positions are residential.

Interested candidates should send a CV and relevant documents or links (and any questions) to bm@sit.org.

Received this today from a heretofore unknown correspondent (I don’t often check Facebook Messenger but just happened to). Name removed (I am not sure he would want me to identify him), text translated from another language into English.

Hello, thanks for your book “Object-Oriented Software Construction” [read in a translation]. I read it after a horrible failure of a project on which I was a consultant. Another consultant was my technical leader. He was truly insufferable but I appreciated him for one reason: his code! I had never seen such “beautiful” program code; he was using principles of genericity, dynamic binding and others, which were totally unknown to me after the lousy programming education I had received. He had insulted me, telling me that I was no developer at all; I was deeply offended since I could feel that he was right. In spite of his unbearable personality I wanted to learn at his side, but he was far too selfish, seeing me just as a competitor, even if a pathetic one. He had a book on the side of his desk… and it’s that book that enabled me to understand where he had learned all those OO design methods. That book, obviously, was yours, and I acquired a copy for myself. I sincerely think that it should be used as textbook in educational institutions. And I really wanted to thank you for writing it. I hope to become a real developer thanks to you. So, thank you.

Note 1: Thanks to you.

Note 2: There is also the intro programming text, Touch of Class (Amazon page).

Note 3 (to my fan club): You are welcome to take advantage of the ideas and there is actually no compelling requirement to be, in addition, “insufferable”.

My group, the Chair of Software Engineering, at the newly created Schaffhausen Institute of Technology has open positions for both PhD students and postdocs. We are looking for candidates with a passion for reliable software and a mix of theoretical knowledge and practical experience in software engineering. Candidates should have degrees in computer science or related fields: a doctorate for postdoc positions, a master’s degree for PhD positions. Postdoc candidates should have a substantial publication record. Experience in one or more of the following fields is a plus:

• Software verification (axiomatic, model-checking, abstract interpretation etc.).
• Advanced techniques of software testing.
• Formal methods, semantics of programming languages, type theory.
• Design by Contract, Eiffel, techniques of correctness-by-construction.
• Cybersecurity.

 Compensation at both levels is attractive. The PhD program is conducted in cooperation with partner universities. 

 Interested candidates should send a CV and relevant documents or links to bm@sit.org. They are also welcome to contact me for details.

About this article: it originated as a series of posts on the Communications of the ACM blog. I normally repost such articles here. (Even though copy-paste is usually not good, there are three reasons for this duplication: the readership seems to be largely disjoint; I can use better formatting, since their blog software is more restrictive than WordPress; and it is good to have a single repository for all my articles, including both those who originated on CACM and those who did not.) The series took the form of nine articles, where each of the first few ended with a quiz, to which the next one, published a couple of days later, provided an answer. Since all these answers are now available it would make no sense to use the same scheme, so I am instead publishing the whole thing as a single article  with nine sections, slightly adapted from the original.

I was too lazy so far to collect all the references into a single list, so numbers such as [1] refer to the list at the end of the corresponding section.

A colleague recently asked me to present a short overview of  axiomatic semantics as a guest lecture in one of his courses. I have been teaching courses on software verification for a long time (see e.g. here), so I have plenty of material; but instead of just reusing it, I decided to spend a bit of time on explaining why it is good to have a systematic approach to software verification. Here is the resulting tutorial.

1. Introduction and attempt #1

Say “software verification” to software professionals, or computer science students outside of a few elite departments, and most of them will think  “testing”. In a job interview, for example, show a loop-based algorithm to a programmer and ask “how would you verify it?”: most will start talking about devising clever test cases.

Far from me to berate testing [1]; in fact, I have always thought that the inevitable Dijkstra quote about testing — that it can only show the presence of errors, not their absence [2] — which everyone seems to take as an indictment and dismissal of testing (and which its author probably intended that way) is actually a fantastic advertisement for testing: a way to find bugs? Yes! Great! Where do I get it?  But that is not the same as verifying the software, which means attempting to ascertain that it has no bugs.

Until listeners realize that verification cannot just mean testing, the best course material on axiomatic semantics or other proof techniques will not attract any interest. In fact, there is somewhere a video of a talk by the great testing and public-speaking guru James Whittaker where he starts by telling his audience not to worry, this won’t be a standard boring lecture, he will not start talking about loop invariants [3]! (Loop invariants are coming in this article, in fact they are one of its central concepts, but in later sections only, so don’t bring the sleeping bags yet.) I decided to start my lecture by giving an example of what happens when you do not use proper verification. More than one example, in fact, as you will see.

A warning about this article: there is nothing new here. I am using an example from my 1990 book Introduction to the Theory of Programming Languages (exercise 9.12). Going even further back, a 1983 “Programming Pearls” Communications of the ACM article by Jon Bentley [4] addresses the same example with the same basic ideas. Yet almost forty years later these ideas are still not widely known among practitioners. So consider these articles as yet another tutorial on fundamental software engineering stuff.

The tutorial is a quiz. We start with a program text:

from

i := 1 ; j := n              — Result initialized to 0.

until i = j loop

m := (i + j) // 2         — Integer division

if t [m] ≤ x then i := m  else  j := m end

end

if x = t [i] then Result := i end

All variables are of integer type. t is an up-sorted array of integers, indexed from 1 to n . We do not let any notation get between friends. A loop from p until e loop q end executes p then, repeatedly: stops if e (the exit condition) is true, otherwise executes q. (Like {p ; while not e do {q}} in some other notations.) “:=” is assignment, “=” equality testing.  “//” is integer division, e.g. 6 //3 = 7 //3 = 2. Result is the name of a special variable whose final value will be returned by this computation (as part of a function, but we only look at the body). Result is automatically initialized to zero like all integer variables, so if execution does not assign anything to Result the function will return zero.

First question: what is this program trying to do?

OK, this is not the real quiz. I assume you know the answer: it is an attempt at “binary search”, which finds an element in the array, or determines its absence, in a sequence of about log₂ (n) steps, rather than n if we were use sequential search.  (Remember we assume the array is sorted.) Result should give us a position where x appears in the array, if it does, and otherwise be zero.

Now for the real quiz: does this program meet this goal?

The answer should be either yes or no. (If no, I am not asking for a correct version, at least not yet, and in any case you can find some in the literature.) The situation is very non-symmetric, we might say Popperian:

• To justify a no answer it suffices of a single example, a particular array t and a particular value x, for which the program fails to set Result as it should.
• To justify a yes answer we need to provide a credible argument that for every t and  x the program sets Result as it should.

Notes to section 1

[1] The TAP conference series (Tests And Proofs), which Yuri Gurevich and I started, explores the complementarity between the two approaches.

[2] Dijkstra first published his observation in 1969. He did not need consider the case of infinite input sets: even for a trivial finite program that multiplies two 32-bit integers, the number of cases to be examined, 2⁶⁴, is beyond human reach. More so today with 64-bit integers. Looking at this from a 2020 perspective, we may note that exhaustive testing of a finite set of cases, which Dijkstra dismissed as impossible in practice, is in fact exactly what the respected model checking verification technique does; not on the original program, but on a simplified — abstracted — version precisely designed to keep the number of cases tractable. Dijkstra’s argument remains valid, of course, for  the original program if non-trivial. And model-checking does not get us out of the woods: while we are safe if its “testing” finds no bug, if it does find one we have to ensure that the bug is a property of the original program rather than an artifact of the abstraction process.

[3] It is somewhere on YouTube, although I cannot find it right now.

[4] Jon Bentley: Programming Pearls: Writing Correct Programs, in Communications of the ACM, vol. 26, no. 12, pp. 1040-1045, December 1983, available for example here.

2. Attempt #2

Was program #1 correct? If so it should yield the correct answer. (An answer is correct if either Result is the index in t of an element equal to x, or Result = 0 and x does not appear in t.)

This program is not correct. To prove that it is not correct it suffices of a single example (test case) for which the program does not  “yield the correct answer”. Assume x = 1 and the array t has two elements both equal to zero (n = 2, remember that arrays are indexed from 1):

t = [0   0]

The successive values of the variables and expressions are:

                                            m       i          j            i + j + 1

After initialization:                   1         2                3

i ≠ j, so enter loop:           1       1        2                 6         — First branch of “if” since t [1] ≤ x
— so i gets assigned the value of m

But then neither of the values of i and j has changed, so the loop will repeat its body identically (taking the first branch) forever. It is not even that the program yields an incorrect answer: it does not yield an answer at all!

Note (in reference to the famous Dijkstra quote mentioned in the first article), that while it is common to pit tests against proofs, a test can actually be a proof: a test that fails is a proof that the program is incorrect. As valid as the most complex mathematical proof. It may not be the kind of proof we like most (our customers tend to prefer a guarantee that the program is correct), but it is a proof all right.

We are now ready for the second attempt:

—  Program attempt #2.

from

i := 1 ; j := n

until i = j or Result > 0  loop

m := (i + j) // 2         — Integer division

if t [m] ≤ x then

i := m  + 1

elseif t [m] = x then

Result := m

else                         — In this case t [m] > x

j := m – 1

end

end

Unlike the previous one this version always changes i or j, so we may hope it does not loop forever. It has a nice symmetry between i and j.

Same question as before: does this program meet its goal?

3. Attempt #3

The question about program #2, as about program #1: was: it right?

Again no.  A trivial example disproves it: n = 1, the array t contains a single element t [1] = 0, x = 0. Then the initialization sets both i and j to 1, i = j holds on entry to the loop which stops immediately, but Result is zero whereas it should be 1 (the place where x appears).

Here now is attempt #3, let us see it if fares better:

—  Program attempt #3.

from

i := 1 ; j := n

until i = j loop

m := (i + j + 1) // 2

if t [m] ≤ x then

i := m  + 1

else

j := m

end

end

if 1  ≤ i  and i ≤ n then Result := i end
       — If not, Result remains 0.

What about this one?

3. Attempt #4 (also includes 3′)

The first two program attempts were wrong. What about the third?

I know, you have every right to be upset at me, but the answer is no once more.

Consider a two-element array t = [0 0] (so n = 2, remember that our arrays are indexed from 1 by convention) and a search value x = 1. The successive values of the variables and expressions are:

                                                  m          i          j            i + j + 1

After initialization:                            1        2           4

i ≠ j, so enter loop:               2           3        2          6                  — First branch of “if” since t [2] < x

i ≠ j,  enter loop again:        3           ⚠                                       — Out-of-bounds memory access!
— (trying to access non-existent t [3])

Oops!

Note that we could hope to get rid of the array overflow by initializing i to 0 rather than 1. This variant (version #3′) is left as a bonus question to the patient reader. (Hint: it is also not correct. Find a counter-example.)

OK, this has to end at some point. What about the following version (#4): is it right?

—  Program attempt #4.

from

i := 0 ; j := n + 1

until i = j loop

m := (i + j) // 2

if t [m] ≤ x then

i := m  + 1

else

j := m

end

end

if 1 ≤ i  and i ≤ n then Result := i end

5. Attempt #5

Yes, I know, this is dragging on. But that’s part of the idea: witnessing how hard it is to get a program right if you just judging by the seat of your pants. Maybe we can get it right this time?

Are we there yet? Is program attempt #4 finally correct?

Sorry to disappoint, but no. Consider a two-element array t = [0 0], so n = 2, and a search value x = 1 (yes, same counter-example as last time, although here we could also use x = 0). The successive values of the variables and expressions are:

                                                 m          i          j            i + j

After initialization:                           0        3           3

i ≠ j, so enter loop:               1           2       3          5            — First branch of “if”

i ≠ j, enter loop again:         2         3        3         6            — First branch again

i = j, exit loop

The condition of the final “if” is true, so Result gets the value 3. This is quite wrong, since there is no element at position 3, and in any case x does not appear in t.

But we are so close! Something like this should work, should it not?

So patience, patience, let us tweak it just one trifle more, OK?

—  Program attempt #5.

from

i := 1 ; j := n + 1

until i ≥ j or Result > 0 loop

m := (i + j) // 2

if t [m] < x then

i := m + 1

elseif  t [m] > x then

j := m

else

Result := m

end

end

Does it work now?

6. Attempt #6

The question about program #5  was the same as before: is it right, is it wrong?

Well, I know you are growing more upset at me with each section, but the answer is still that this program is wrong. But the way it is wrong is somewhat specific; and it applies, in fact, to all previous variants as well.

This particular wrongness (fancy word for “bug”) has a history. As I pointed out in the first article, there is a long tradition of using binary search to illustrate software correctness issues. A number of versions were published and proved correct, including one in the justly admired Programming Pearls series by Jon Bentley. Then in 2006 Joshua Bloch, then at Google, published a now legendary blog article [2] which showed that all these versions suffered from a major flaw: to obtain m, the approximate mid-point between i and j, they compute

(i + j) // 2

which, working on computer integers rather than mathematical integers, might overflow! This in a situation in which both i and j, and hence m as well, are well within the range of the computer’s representable integers, 2^-n to 2ⁿ (give or take 1) where n is typically 31 or, these days, 63, so that there is no conceptual justification for the overflow.

In the specification that I have used for this article, i starts at 1, so the problem will only arise for an array that occupies half of the memory or more, which is a rather extreme case (but still should be handled properly). In the general case, it is often useful to use arrays with arbitrary bounds (as in Eiffel), so we can have even a small array, with high indices, for which the computation will produce an overflow and bad results.

The Bloch gotcha is a stark reminder that in considering the correctness of programs we must include all relevant aspects and consider programs as they are executed on a real computer, not as we wish they were executed in an ideal model world.

(Note that Jon Bentley alluded to this requirement in his original article: while he did not explicitly mention integer overflow, he felt it necessary to complement his proof by the comment that that  “As laborious as our proof of binary search was, it is still unfinished by some standards. How would you prove that the program is free of runtime errors (such as division by zero, word overflow, or array indices out of bounds)?” Prescient words!)

It is easy to correct the potential arithmetic overflow bug: instead of (i + j) // 2, Bloch suggested we compute the average as

i + (j – i) // 2

which is the same from a mathematician’s viewpoint, and indeed will compute the same value if both variants compute one, but will not overflow if both i and j are within range.

So we are ready for version 6, which is the same as version 5 save for that single change:

—  Program attempt #6.

from

i := 1 ; j := n + 1

until i ≥ j or Result > 0 loop

m := i + (j – i) // 2

if t [m] < x then

i := m + 1

elseif  t [m] > x then

j := m

else

Result := m

end

end

Now is probably the right time to recall the words by which Donald Knuth introduces binary search in the original 1973 tome on Sorting and Searching of his seminal book series The Art of Computer Programming:

Although the basic idea of binary search is comparatively straightforward, the details can be somewhat tricky, and many good programmers have done it wrong the first few times they tried.

Do you need more convincing? Be careful what you answer, I have more variants up my sleeve and can come up with many more almost-right-but-actually-wrong program attempts if you nudge me. But OK, even the best things have an end. This is not the last section yet, but that was the last program attempt. To the naturally following next question in this running quiz,  “is version 6 right or wrong”, I can provide the answer: it is, to the best of my knowledge, a correct program. Yes! [3].

But the quiz continues. Since answers to the previous questions were all  that the programs were not correct, it sufficed in each case to find one case for which the program did not behave as expected. Our next question is of a different nature: can you find an argument why version #6 is correct?

References for section 6

[1] (In particular) Jon Bentley: Programming Pearls — Writing Correct Programs, in Communications of the ACM, vol. 26, no. 12, December 1983, pages 1040-1045, available here.

[2] Joshua Bloch: Extra, Extra — Read All About It: Nearly All Binary Searches and Mergesorts are Broken, blog post, on the Google AI Blog, 2 June 2006, available here.

[3] A caveat: the program is correct barring any typos or copy-paste errors — I am starting from rigorously verified programs (see the next posts), but the blogging system’s UI and text processing facilities are not the best possible for entering precise technical text such as code. However carefully I check, I cannot rule out a clerical mistake, which of course would be corrected as soon as it is identified.

7. Using a program prover

Preceding sections presented candidate binary search algorithms and asked whether they are correct. “Correct” means something quite precise: that for an array t and a value x, the final value of the variable Result is a valid index of t (that is to say, is between 1 and n, the size of t) if and only if x appears at that index in t.

The last section boldly stated that program attempt #6 was correct. The question was: why?

In the case of the preceding versions, which were incorrect, you could prove that property, and I do mean prove, simply by exhibiting a single counter-example: a single t and x for which the program does not correctly set Result. Now that I asserting the program to be correct, one example, or a million examples, do not suffice. In fact they are almost irrelevant. Test as much as you like and get correct results every time, you cannot get rid of the gnawing fear that if you had just tested one more time after the millionth test you would have produced a failure. Since the set of possible tests is infinite there is no solution in sight [1].

We need a proof.

I am going to explain that proof in the next section, but before that I would like to give you an opportunity to look at the proof by yourself. I wrote in one of the earlier articles that most of what I have to say was already present in Jon Bentley’s 1983 Programming Pearls contribution [2], but a dramatic change did occur in the four decades since: the appearance of automated proof system that can handle significant, realistic programs. One such system, AutoProof, was developed at the Chair of Software engineering at ETH Zurich [3] (key project members were Carlo Furia, Martin Nordio, Nadia Polikarpova and Julian Tschannen, with initial contributions by Bernd Schoeller) on the basis of the Boogie proof technology from Microsoft Research).

AutoProof is available for online use, and it turns out that one of the basic tutorial examples is binary search. You can go to the corresponding page and run the proof.

I am going to let you try this out (and, if you are curious, other online AutoProof examples as well) without too many explanations; those will come in the next section. Let me simply name the basic proof technique: loop invariant. A loop invariant is a property INV associated with a loop, such that:

• A. After the loop’s initialization, INV will hold.
• B. One execution of the loop’s body, if started with INV satisfied (and the loop’s exit condition not satisfied, otherwise we wouldn’t be executing the body!), satisfies INV again when it terminates.

This idea is of course the same as that of a proof by induction in mathematics: the initialization corresponds to the base step (proving that P (0) holds) and the body property to the induction step (proving that from P (n) follows P (n + 1). With a traditional induction proof we deduce that the property (P (n)) holds for all integers. For the loop, we deduce that when the loop finishes its execution:

• The invariant still holds, since executing the loop means executing the initialization once then the loop body zero or more times.
• And of course the exit condition also holds, since otherwise we would still be looping.

That is how we prove the correctness of a loop: the conjunction of the invariant and the exit condition must yield the property that we seek (in the example, the property, stated above of Result relative to t and x).

We also need to prove that the loop does terminate. This part involves another concept, the loop’s variant, which I will explain in the next section.

For the moment I will not say anything more and let you look at the AutoProof example page (again, you will find it here), run the verification, and read the invariant and other formal elements in the code.

To “run the verification” just click the Verify button on the page. Let me emphasize (and emphasize again and again and again) that clicking Verify will not run the code. There is no execution engine in AutoProof, and the verification does not use any test cases. It processes the text of the program as it appears on the page and below. It applies mathematical techniques to perform the proof; the core property to be proved is that the proposed loop invariant is indeed invariant (i.e. satisfies properties A and B above).

The program being proved on the AutoProof example page is version #6 from the last section, with different variable names. So far for brevity I have used short names such as i, j and m but the program on the AutoProof site applies good naming practices with variables called low, up, middle and the like. So here is that version again with the new variable names:

—  Program attempt #7  (identical to #6 with different variable names) .

from

low := 0 ; up := n

until low ≥ up or Result > 0 loop

middle := low + ((up – low) // 2)

if a [middle] < value then      — The array is now called a rather than t

low := middle + 1

elseif  a [middle] > value then

up := middle

else

Result := middle

end

end

This is exactly the algorithm text on the AutoProof page, the one that you are invited to let AutoProof verify for you. I wrote “algorithm text” rather than “program text” because the actual program text (in Eiffel) includes variant and invariant clauses which do not affect the program’s execution but make the proof possible.

Whether or not these concepts (invariant, variant, program proof) are completely new to you, do try the prover and take a look at the proof-supporting clauses. In the next article I will remove any remaining mystery.

Note and references for section 7

[1] Technically the set of possible [array, value] pairs is finite, but of a size defying human abilities. As I pointed out in the first section, the “model checking” and “abstract interpretation” verification techniques actually attempt to perform an exhaustive test anyway, after drastically reducing the size of the search space. That will be for some other article.

[2]  Jon Bentley: Programming Pearls: Writing Correct Programs, in Communications of the ACM, vol. 26, no. 12, pp. 1040-1045, December 1983, available for example here.

[3] The AutoProof page contains documentations and numerous article references.

8. Understanding the proof

The previous section invited you to run the verification on the AutoProof tutorial page dedicated to the example. AutoProof is an automated proof system for programs. This is just a matter of clicking  “Verify”, but more importantly, you should read the annotations added to the program text, particularly the loop invariant, which make the verification possible. (To avoid any confusion let me emphasize once more that clicking “Verify” does not run the program, and that no test cases are used; the effect is to run the verifier, which attempts to prove the correctness of the program by working solely on the program text.)

Here is the program text again, reverting for brevity to the shorter identifiers (the version on the AutoProof page has more expressive ones):

from

i := 1 ; j := n + 1

until i ≥ j or Result > 0 loop

m := i + (j – i) // 2

if t [m] < x then

i := m + 1

elseif  t [m] > x then

j := m

else

Result := m

end

end

Let us now see what makes the proof possible. The key property is the loop invariant, which reads

A:   1  ≤ i  ≤ j  ≤ n + 1
B:   0  ≤ Result  ≤ n
C:   ∀ k: 1 .. i –1  |  t [k] < x
D:   ∀ k: j .. n  |  t [k] > x
E:    (Result > 0)   ⇒   (t [Result] = x)

The notation is slightly different on the Web page to adapt to the Eiffel language as it existed at the time it was produced; in today’s Eiffel you can write the invariant almost as shown above. Long live Unicode, allowing us to use symbols such as ∀ (obtained not by typing them but by using smart completion, e.g. you start typing “forall” and you can select the ∀ symbol that pops up), ⇒ for  “implies” and many others

Remember that the invariant has to be established by the loop’s initialization and preserved by every iteration. The role of each of its clauses is as follows:

• A: keep the indices in range.
• B: keep the variable Result, whose final value will be returned by the function, in range.
• C and D: eliminate index intervals in which we have determined that the sought value, x, does not appear. Before i, array values are smaller; starting at j, they are greater. So these two intervals, 1..i and j..n, cannot contain the sought value. The overall idea of the algorithm (and most other search algorithms) is to extend one of these two intervals, so as to narrow down the remaining part of 1..n where x may appear.
• E: express that as soon as we find a positive (non-zero) Result, its value is an index in the array (see B) where x does appear.

Why is this invariant useful? The answer is that on exit it gives us what we want from the algorithm. The exit condition, recalled above, is

i ≥ j or Result > 0

Combined with the invariant, it tells us that on exit one of the following will hold:

• Result > 0, but then because of E we know that x appears at position Result.
• i < j, but then A,  C and D  imply that x does not appear anywhere in t. In that case it cannot be true that Result > 0, but then because of B Result must be zero.

What AutoProof proves, mechanically, is that under the function’s precondition (that the array is sorted):

• The initialization ensures the invariant.
• The loop body, assuming that the invariant is satisfied but the exit condition is not, ensures the loop invariant again after it executes.
• The combination of the invariant and the exit condition ensures, as just explained, the postcondition of the function (the property that Result will either be positive and the index of an element equal to x, or zero with the guarantee that x appears nowhere in t).

Such a proof guarantees the correctness of the program if it terminates. We (and AutoProof) must prove separately that it does terminate. The technique is simple: find a “loop variant”, an integer quantity v  which remains non-negative throughout the loop (in other words, the loop invariant includes or implies v ≥ 0) and decreases on each iteration, so that the loop cannot continue executing forever. An obvious variant here is j – i + 1 (where the + 1 is needed because j – i may go down to -1 on the last iteration if x does not appear in the array). It reflects the informal idea of the algorithm: repeatedly decrease an interval i .. j – 1 (initially, 1 .. n) guaranteed to be such that x appears in t if and only if it appears at an index in that interval. At the end, either we already found x or the interval is empty, implying that x does not appear at all.

A great reference on variants and the techniques for proving program termination is a Communications of the ACM article of 2011: [3].

The variant gives an upper bound on the number of iterations that remain at any time. In sequential search, j – i + 1 would be our best bet; but for binary search it is easy to show that  log₂  (j – i + 1) is also a variant, extending the proof of correctness with a proof of performance (the key goal of binary search being to ensure a logarithmic rather than linear execution time).

This example is, I hope, enough to highlight the crucial role of loop invariants and loop variants in reasoning about loops. How did we get the invariant? It looks like I pulled it out of a hat. But in fact if we go the other way round (as advocated in classic books [1] [2]) and develop the invariant and the loop together the process unfolds itself naturally and there is nothing mysterious about the invariant.

Here I cannot resist quoting (thirty years on!) from my own book Introduction to the Theory of Programming Languages [4]. It has a chapter on axiomatic semantics (also known as Hoare logic, the basis for the ideas used in this discussion), which I just made available: see here [5]. Its exercise 9.12 is the starting point for this series of articles. Here is how the book explains how to design the program and the invariant [6]:

In the general case [of search, binary or not] we aim for a loop body of the form

m := ‘‘Some value in 1.. n such that i ≤ m < j’’;

if t [m] ≤ x then

i := m + 1

else

j := m

end

It is essential to get all the details right (and easy to get some wrong):

• The instruction must always decrease the variant j – i, by increasing i or decreasing j. If the the definition of m specified just m ≤ j rather than m < j, the second branch would not meet this goal.
•  This does not transpose directly to i: requiring i < m < j would lead to an impossibility when j – i is equal to 1. So we accept i ≤ m but then we must take m + 1, not m, as the new value of i in the first branch.
•  The conditional’s guards are tests on t [m], so m must always be in the interval 1 . . n. This follows from the clause 0 ≤ i ≤ j ≤ n + 1 which is part of the invariant.
•  If this clause is satisfied, then m ≤ n and m > 0, so the conditional instruction indeed leaves this clause invariant.
• You are invited to check that both branches of the conditional also preserve the rest of the invariant.
• Any policy for choosing m is acceptable if it conforms to the above scheme. Two simple choices are i  and j – 1; they lead to variants of the sequential search algorithm [which the book discussed just before binary search].

For binary search, m will be roughly equal to the average of i and j.

“Roughly” because we need an integer, hence the // (integer division).

In the last section, I will reflect further on the lessons we can draw from this example, and the practical significance of the key concept of invariant.

References and notes for section 8

[1] E.W. Dijkstra: A Discipline of Programming, Prentice Hall, 1976.

[2] David Gries: The Science of Programming, Springer, 1989.

[3] Byron Cook, Andreas  Podelski and Andrey Rybalchenko: Proving program termination, in Communications of the ACM, vol. 54, no. 11, May 2011, pages 88-98, available here.

[4] Bertrand Meyer, Introduction to the Theory of Programming Languages, Prentice Hall, 1990. The book is out of print but can be found used, e.g. on Amazon. See the next entry for an electronic version of two chapters.

[5] Bertrand Meyer Axiomatic semantics, chapter 9 from [3], available here. Note that the PDF was reconstructed from an old text-processing system (troff); the figures could not be recreated and are missing. (One of these days I might have the patience of scanning them from a book copy and adding them. Unless someone wants to help.) I also put online, with the same caveat, chapter 2 on notations and mathematical basis: see here.

[6] Page 383 of [4] and [5]. The text is verbatim except a slight adaptation of the programming notation and a replacement of the variables: i in the book corresponds to i – 1 here, and j to j – 1. As a matter of fact I prefer the original conventions from the book (purely as a matter of taste, since the two are rigorously equivalent), but I changed here to the conventions of the program as it appears in the AutoProof page, with the obvious advantage that you can verify it mechanically. The text extract is otherwise exactly as in the 1990 book.

9. Lessons learned

What was this journey about?

We started with a succession of attempts that might have “felt right” but were in fact all wrong, each in its own way: giving the wrong answer in some cases, crashing (by trying to access an array outside of its index interval) in some cases, looping forever in some cases. Always “in some cases”,  evidencing the limits of testing, which can never guarantee that it exercises all the problem cases. A correct program is one that works in all cases. The final version was correct; you were able to prove its correctness with an online tool and then to understand (I hope) what lies behind that proof.

To show how to prove such correctness properties, I have referred throughout the series to publications from the 1990s (my own Introduction to The Theory of Programming Languages), the 1980s (Jon Bentley’s Programming Pearls columns, Gries’s Science of Programming), and even the 1970s (Dijkstra’s Discipline of Programming). I noted that the essence of my argument appeared in a different form in one of Bentley’s Communications articles. What is the same and what has changed?

The core concepts have been known for a long time and remain applicable: assertion, invariant, variant and a few others, although they are much better understood today thanks to decades of theoretical work to solidify the foundation. Termination also has a more satisfactory theory.

On the practical side, however, the progress has been momentous. Considerable engineering has gone into making sure that the techniques scaled up. At the time of Bentley’s article, binary search was typical of the kind of programs that could be proved correct, and the proof had to proceed manually. Today, we can tackle much bigger programs, and use tools to perform the verification.

Choosing binary search again as an example today has the obvious advantage that everyone can understand all the details, but should not be construed as representative of the state of the art. Today’s proof systems are far more sophisticated. Entire operating systems, for example, have been mechanically (that is to say, through a software tool) proved correct. In the AutoProof case, a major achievement was the proof of correctness [1] of an entire data structure (collections) library, EiffelBase 2. In that case, the challenge was not so much size (about 8,000 source lines of code), but the complexity of both:

• The scope of the verification, involving the full range of mechanisms of a modern object-oriented programming language, with classes,  inheritance (single and multiple), polymorphism, dynamic binding, generics, exception handling etc.
• The code itself, using sophisticated data structures and algorithms, involving in particular advanced pointer manipulations.

In both cases, progress has required advances on both the science and engineering sides. For example, the early work on program verification assumed a bare-bones programming language, with assignments, conditionals, loops, routines, and not much more. But real programs use many other constructs, growing ever richer as programming languages develop. To cover exception handling in AutoProof required both theoretical modeling of this construct (which appeared in [2]) and implementation work.

More generally, scaling up verification capabilities from the small examples of 30 years ago to the sophisticated software that can be verified today required the considerable effort of an entire community. AutoProof, for example, sits at the top of a tool stack relying on the Boogie environment from Microsoft Research, itself relying on the Z3 theorem prover. Many person-decades of work make the result possible.

Beyond the tools, the concepts are esssential. One of them, loop invariants, has been illustrated in the final version of our program. I noted in the first article the example of a well-known expert and speaker on testing who found no better way to announce that a video would not be boring than  “relax, we are not going to talk about loop invariants.” Funny perhaps, but unfair. Loop invariants are one of the most beautiful concepts of computer science. Not so surprisingly, because loop invariants are the application to programming of the concept of mathematical induction. According to the great mathematician Henri Poincaré, all of mathematics rests on induction; maybe he exaggerated, maybe not, but who would think of teaching mathematics without explaining induction? Teaching programming without explaining loop invariants is no better.

Below is an illustration (if you will accept my psychedelic diagram) of what a loop is about, as a problem-solving technique. Sometimes we can get the solution directly. Sometimes we identify several steps to the solution; then we use a sequence (A ; B; C). Sometimes we can find two (or more) different ways of solving the problem in different cases; then we use a conditional (if c then A else B end). And sometimes we can only get a solution by getting closer repeatedly, not necessarily knowing in advance how many times we will have to advance towards it; then, we use a loop.

We identify an often large (i.e. very general) area where we know the solution will lie; we call that area the loop invariant. The solution or solutions (there may be more than one) will have to satisfy a certain condition; we call it the exit condition. From wherever we are, we shoot into the invariant region, using an appropriate operation; we call it the initialization. Then we execute as many times as needed (maybe zero if our first shot was lucky) an operation that gets us closer to that goal; we call it the loop body. To guarantee termination, we must have some kind of upper bound of the distance to the goal, decreasing each time discretely; we call it the loop variant.

This explanation is only an illustration, but I hope it makes the ideas intuitive. The key to a loop is its invariant. As the figure suggests, the invariant is always a generalization of the goal. For example, in binary search (and many other search algorithms, such as sequential search), our goal is to find a position where either x appears or, if it does not, we can be sure that it appears nowhere. The invariant says that we have an interval with the same properties (either x appears at a position belonging to that interval or, if it does not, it appears nowhere). It obviously includes the goal as a special case: if the interval has length 1, it defines a single position.

An invariant should be:

1. Strong enough that we can devise an exit condition which in the end, combined with the invariant, gives us the goal we seek (a solution).
2. Weak enough that we can devise an initialization that ensures it (by shooting into the yellow area) easily.
3. Tuned so that we can devise a loop body that, from a state satifying the invariant, gets us to a new one that is closer to the goal.

In the example:

1. The exit condition is simply that the interval’s length is 1. (Technically, that we have computed Result as the single interval element.) Then from the invariant and the exit condition, we get the goal we want.
2. Initialization is easy, since we can just take the initial interval to be the whole index range of the array, which trivially satisfies the invariant.
3. The loop body simply decreases the length of the interval (which can serve as loop variant to ensure termination). How we decrease the length depends on the search strategy; in sequential search, each iteration decreases the length by 1, correct although not fast, and binary search decreases it by about half.

The general scheme always applies. Every loop algorithm is characterized by an invariant. The invariant may be called the DNA of the algorithm.

To demonstrate the relevance of this principle, my colleagues Furia, Velder, and I published a survey paper [6] in ACM Computing Surveys describing the invariants of important algorithms in many areas of computer science, from search algorithms to sorting (all major algorithms), arithmetic (long integer addition, squaring), optimization and dynamic programming  (Knapsack, Levenshtein/Edit distance), computational geometry (rotating calipers), Web (Page Rank)… I find it pleasurable and rewarding to go deeper into the basis of loop algorithms and understand their invariants; like a geologist who does not stop at admiring the mountain, but gets to understand how it came to be.

Such techniques are inevitable if we want to get our programs right, the topic of this article. Even putting aside the Bloch average-computation overflow issue, I started with 5 program attempts, all kind of friendly-looking but wrong in different ways. I could have continued fiddling with the details, following my gut feeling to fix the flaws and running more and more tests. Such an approach can be reasonable in some cases (if you have an algorithm covering a well-known and small set of cases), but will not work for non-trivial algorithms.

Newcomers to the concept of loop invariant sometimes panic: “this is all fine, you gave me the invariants in your examples, how do I find my own invariants for my own loops?” I do not have a magic  recipe (nor does anyone else), but there is no reason to be scared. Once you have understood the concept and examined enough examples (just a few of those in [6] should be enough), writing the invariant at the same time as you are devising a loop will come as a second nature to you.

As the fumbling attempts in the first few sections should show, there is not much of an alternative. Try this approach. If you are reaching these final lines after reading what preceded them, allow me to thank you for your patience, and to hope that this rather long chain of reflections on verification will have brought you some new insights into the fascinating challenge of writing correct programs.

References

[1] Nadia Polikarpova, Julian Tschannen, and Carlo A. Furia: A Fully Verified Container Library, in Proceedings of 20th International Symposium on Formal Methods (FM 15), 2015. (Best paper award.)

[2] Martin Nordio, Cristiano Calcagno, Peter Müller and Bertrand Meyer: A Sound and Complete Program Logic for Eiffel, in Proceedings of TOOLS 2009 (Technology of Object-Oriented Languages and Systems), Zurich, June-July 2009, eds. M. Oriol and B. Meyer, Springer LNBIP 33, June 2009.

[3] Boogie page at MSR, see here for publications and other information.

[4] Z3 was also originally from MSR and has been open-sourced, one can get access to publications and other information from  its Wikipedia page.

[5] Carlo Furia, Bertrand Meyer and Sergey Velder: Loop invariants: Analysis, Classification and Examples, in ACM Computing Surveys, vol. 46, no. 3, February 2014. Available here.

[6] Dynamic programming is a form of recursion removal, turning a recursive algorithm into an iterative one by using techniques known as “memoization” and  “bottom-up computation” (Berry). In this transformation, the invariant plays a key role. I will try to write this up some day as it is a truly elegant and illuminating explanation.

As part of the continuation of the ERC Advanced Investigator Grant project “Concurrency Made Easy” (started at ETH Zurich, see the project pages at cme.ethz.ch), I have positions at Politecnico di Milano for:

• Postdocs (having a doctoral degree)
• Research associates (officially: “Assegno di Ricerca”, with the requirement of having a master degree), which can lead to a PhD position.

The deadline for applications is October 11. Please contact me directly if interested. What I expect:

• The requisite degrees as stated above.
• Innovative and enterprising spirit, passion for quality work in software engineering.
• Either or both of excellent programming abilities and strong CS theoretical background.
• Knowledge of as many of possible of: object-oriented programming, concurrency/parallelism, software verification/formal methods, Eiffel.
• Familiarity with the basics of the project as described in the project pages at the URL above.

The 2016 session of the LASER summer school, now in its 13th edition, has just been announced. The theme is new for the school, and timely: software for robotics. Below is the announcement.

School site: here

The 2016 LASER summer school will be devoted to Software for Robotics. It takes place from 10 to 18 September in the magnificent setting of the Hotel del Golfo in Procchio, Elba Island, Italy.

Robotics is progressing at an amazing pace, bringing improvements to almost areas of human activity. Today’s robotics systems rely ever more fundamentally on complex software, raising difficult issues. The LASER 2016 summer school both covers the current state of robotics software technology and open problems. The lecturers are top international experts with both theoretical contributions and major practical achievements in developing robotics systems.
The LASER school is intended for professionals from the industry (engineers and managers) as well as university researchers, including PhD students. Participants learn about the most important software technology advances from the pioneers in the field. The school’s focus is applied, although theory is welcome to establish solid foundations. The format of the school favors extensive interaction between participants and speakers.
The speakers include:

• Joydeep Biswas, University of Massachussetts, on Development, debugging, and maintenance of deployed robots
• Davide Brugali, University of Bergamo, on Managing software variability in robotic control systems
• Nenad Medvidovic, University of Southern California, on Software Architectures of Robotics Systems
• Bertrand Meyer, Politecnico di Milano and Innopolis University, with Jiwon Shin, on Concurrent Object-Oriented Robotics Software: Concepts, Framework and Applications
• Issa Nesnas, NASA Jet Propulsion Laboratory, on Experiences from robotic software development for research and planetary flight robots
• Richard Vaughan, Simon Fraser University

Organized by Politecnico di Milano, the school takes place at the magnificent Hotel del Golfo (http://www.hoteldelgolfo.it/) in Golfo di Procchio, Elba. Along with an intensive scientific program, participants will have time to enjoy the natural and cultural riches of this history-laden jewel of the Mediterranean.

For more information about the school, the speakers and registration see here.

.

— Bertrand Meyer

Programming, wrote Dijkstra many years ago, is a branch of applied mathematics. That is only half of the picture: the other half is engineering, and this dual nature of programming is part of its attraction.

Descriptions of the mathematical side are generally, in my view, too complicated. This article [1] presents a mathematical theory of programs and programming based on concepts taught in high school: elementary set theory. The concepts covered include:

• Programming.
• Specification.
• Refinement.
• Non-determinism.
• Feasibility.
• Correctness.
• Programming languages.
• Kinds of programs: imperative, functional, object-oriented.
• Concurrency (small-step and large-step)
• Control structures (compound, if-then-else and Dijkstra-style conditional, loop).
• State, store and environment.
• Invariants.
• Notational conventions for building specifications and programs incrementally.
• Loop invariants and variants.

One of the principal ideas is that a program is simply the description of a mathematical relation. The program text is a rendering of that relation. As a consequence, one may construct programming languages simply as notations to express certain kinds of mathematics. This approach is the reverse of the usual one, where the program text and its programming languages are the starting point and the center of attention: theoreticians develop techniques to relate them to mathematical concepts. It is more effective to start from the mathematics (“unparsing” rather than parsing).

All the results (74 properties expressed formally, a number of others in the text) are derived as theorems from rules of elementary set theory; there are no new axioms whatsoever.

The paper also has a short version [2], omitting proofs and many details.

References

[1] Theory of Programs, available here.
[2] Theory of Programs, short version of [1] (meant for quick understanding of the ideas, not for publication), available here.

Among the open problems of verification, particularly the verification of object-oriented programs, one of the most vexing is framing: how to specify and verify what programs element do not change. Continuing previous work, this article presents a “double frame inference” method, automatic on both sides the specification and verification sides. There is no need to write frame specifications: they will be inferred from routine postconditions. For verification, the method computes the set of actually changed properties through a “change calculus”, itself based on the previously developed alias calculus.

Some verification techniques, such as Hoare-style proofs, require significant annotation effort and potentially yield full functional verification; others, such as model checking and abstract interpretation, have more limited goals but seek full automation. Framing, in my opinion, should be automatic, freeing the programmer-verifier to devote the annotation effort to truly interesting properties.

Reference

[1] Bertrand Meyer: Framing the Frame Problem, in Dependable Software Systems, Proceedings of August 2014 Marktoberdorf summer school, eds. Alexander Pretschner, Manfred Broy and Maximilian Irlbeck, NATO Science for Peace and Security, Series D: Information and Communication Security, Springer, 2015 (to appear), pages 174-185; preprint available here.

In support of his view of software methodology, Leslie Lamport likes to use the example of non-recursive Quicksort. Independently of the methodological arguments, his version of the algorithm should be better known. In fact, if I were teaching “data structures and algorithms” I would consider introducing it first.

As far as I know he has not written down his version in an article, but he has presented it in lectures; see [1]. His trick is to ask the audience to give a non-recursive version of Quicksort, and of course everyone starts trying to remove the recursion, for example by making the stack explicit or looking for invertible functions in calls. But his point is that recursion is not at all fundamental in Quicksort. The recursive version is a specific implementation of a more general idea.

Lamport’s version — let us call it Lampsort —is easy to express in Eiffel. We may assume the following context:

a: ARRAY [G -> COMPARABLE]        — The array to be sorted.
pivot: INTEGER                                      —  Set by partition.
picked: INTEGER_INTERVAL            — Used by the sorting algorithm, see below.
partition (i, j: INTEGER)
……..require      — i..j is a sub-interval of the array’s legal indexes:
……..……..i < j
……..……..i >= a.lower
……..……..j <= a.upper
……..do
……..……..… Usual implementation of partition …
……..ensure     — The expected effect of partition:
……..……..pivot >= i
……..……..pivot < j
……..……..— a [i..j] has been reshuffled so that elements in i..pivot are less than
……..……..— or equal to those in pivot+1 .. j.
……..end

We do not write the implementation of partition since the point of the present discussion is the overall algorithm. In the usual understanding, that algorithm consists of doing nothing if the array has no more than one element, otherwise performing a partition and then recursively calling itself on the two resulting intervals. The implementation can take advantage of parallelism by forking the recursive calls out to different processors. That presentation, says Lamport, describes only a possible implementation. The true Quicksort is more general. The algorithm works on a set not_sorted of integer intervals i..j such that the corresponding array slices a [i..j] are the only ones possibly not sorted; the goal of the algorithm is to make not_sorted empty, since then we know the entire array is sorted. In Eiffel we declare this set as:

not_sorted: SET [INTEGER_INTERVAL]

The algorithm initializes not_sorted to contain a single element, the entire interval; at each iteration, it removes an interval from the set, partitions it if that makes sense (i.e. the interval has more than one element), and inserts the resulting two intervals into the set. It ends when not_sorted is empty. Here it is:

……..from                                 — Initialize interval set to contain a single interval, the array’s entire index range:
……..…..create not_sorted.make_one (a.lower |..| a.upper)….         ..……..
……..invariant
……..…..— See below
……..until
……..…..not_sorted.is_empty                                                            — Stop when there are no more intervals in set
……..loop
……..…..picked := not_sorted.item                                                     — Pick an interval from (non-empty) interval set.
……..……if picked.count > 1 then                                                      — (The precondition of partition holds, see below.)
……..……..…..partition (picked.lower, picked.upper)                 — Split, moving small items before & large ones after pivot.
……..……..…..not_sorted.extend (picked.lower |..| pivot)            — Insert new intervals into the set of intervals: first
……..……....…not_sorted.extend (pivot + 1 |..| picked.upper)     — and second.
……..……end
……..…...not_sorted.remove (picked)                                               — Remove interval that was just partitioned.
…….end

Eiffel note: the function yielding an integer interval is declared in the library class INTEGER using the operator |..| (rather than just  ..).

The query item from SET, with the precondition not is_empty,  returns an element of the set. It does not matter which element. In accordance with the Command-Query Separation principle, calling item does not modify the set; to remove the element you have to use the command remove. The command extend adds an element to the set.

The abstract idea behind Lampsort, explaining why it works at all, is the following loop invariant (see [2] for a more general discussion of how invariants provide the basis for understanding loop algorithms). We call “slice” of an array a non-empty contiguous sub-array; for adjacent slices we may talk of concatenation; also, for slices s and t,  s <= t means that every element of s is less than or equal to every element of t. The invariant is:

a is the concatenation of the members of a set slices of disjoint slices, such that:
– The elements of a are a permutation of its original elements.
– The index range of any member  of slices having more than one element is in not_sorted.
– For any adjacent slices s and t (with s before t), s <= t.

The first condition (conservation of the elements modulo permutation) is a property of partition, the only operation that can modify the array. The rest of the invariant is true after initialization (from clause) with slices made of a single slice, the full array. The loop body maintains it since it either removes a one-element interval from not_sorted (slices loses the corresponding slice) or performs partition with the effect of partitioning one slice into two adjacent ones satisfying s <= t, whose intervals replace the original one in not_sorted. On exit, not_sorted is empty, so slices is a set of one-element slices, each less than or equal to the next, ensuring that the array is sorted.

The invariant also ensures that the call to partition satisfies that routine’s precondition.

The Lampsort algorithm is a simple loop; it does not use recursion, but relies on an interesting data structure, a set of intervals. It is not significantly longer or more difficult to understand than the traditional recursive version

sort (i, j: INTEGER)
……..require
……..……..i <= j
……..……..i >= a.lower
……..……..j <= a.upper
……..do
……..……if j > i then                    — Note that precondition of partition holds.
……..……..…..partition (i, j)         — Split into two slices s and t such that s <= t.
……..……..…..sort (i, pivot)          — Recursively sort first slice.
……..……..…..sort (pivot+1, j)      — Recursively sort second slice.
……..……end……..…..
……..end

Lampsort, in its author’s view, captures the true idea of Quicksort; the recursive version, and its parallelized variants, are only examples of possible implementations.

I wrote at the start that the focus of this article is Lampsort as an algorithm, not issues of methodology. Let me, however, give an idea of the underlying methodological debate. Lamport uses this example to emphasize the difference between algorithms and programs, and to criticize the undue attention being devoted to programming languages. He presents Lampsort in a notation which he considers to be at a higher level than programming languages, and it is for him an algorithm rather than a program. Programs will be specific implementations guided in particular by efficiency considerations. One can derive them from higher-level versions (algorithms) through refinement. A refinement process may in particular remove or restrict non-determinism, present in the above version of Lampsort through the query item (whose only official property is that it returns an element of the set).

The worldview underlying the Eiffel method is almost the reverse: treating the whole process of software development as a continuum; unifying the concepts behind activities such as requirements, specification, design, implementation, verification, maintenance and evolution; and working to resolve the remaining differences, rather than magnifying them. Anyone who has worked in both specification and programming knows how similar the issues are. Formal specification languages look remarkably like programming languages; to be usable for significant applications they must meet the same challenges: defining a coherent type system, supporting abstraction, providing good syntax (clear to human readers and parsable by tools), specifying the semantics, offering modular structures, allowing evolution while ensuring compatibility. The same kinds of ideas, such as an object-oriented structure, help on both sides. Eiffel as a language is the notation that attempts to support this seamless, continuous process, providing tools to express both abstract specifications and detailed implementations. One of the principal arguments for this approach is that it supports change and reuse. If everything could be fixed from the start, maybe it could be acceptable to switch notations between specification and implementation. But in practice specifications change and programs change, and a seamless process relying on a single notation makes it possible to go back and forth between levels of abstraction without having to perform repeated translations between levels. (This problem of change is, in my experience, the biggest obstacle to refinement-based approaches. I have never seen a convincing description of how one can accommodate specification changes in such a framework without repeating the whole process. Inheritance, by the way, addresses this matter much better.)

The example of Lampsort in Eiffel suggests that a good language, equipped with the right abstraction mechanisms, can be effective at describing not only final implementations but also abstract algorithms. It does not hurt, of course, that these abstract descriptions can also be executable, at the possible price of non-optimal performance. The transformation to an optimal version can happen entirely within the same method and language.

Quite apart from these discussions of software engineering methodology, Lamport’s elegant version of Quicksort deserves to be known widely.

References

[1] Lamport video here, segment starting at 0:32:34.
[2] Carlo Furia, Bertrand Meyer and Sergey Velder: Loop invariants: Analysis, Classification and Examples, in ACM Computing Surveys, September 2014, preliminary text here.

My colleagues and I have just finished recording our new MOOC (online course), an official ETH offering on the EdX platform. The preview is available [1] and the course will run starting in September.

As readers of this blog know, I  have enthusiastically, under the impulsion of Marco Piccioni at ETH, embraced MOOC technology to support and spread our courses. The particular target has been the introduction to programming that I have taught for over a decade at ETH based on the Touch of Class textbook [2]. In February this blog announced [3] the release of our first MOOC, embodying the essentials of our ETH course and making it available not only to ETH students but to the whole world. The course does not just include video lectures: it also supports active student participation through online exercises and programs that can be compiled and tested on the cloud, with no software installation. These advanced features result from our research on support for distributed software development (by Christian Estler and Martin Nordio, with Carlo Furia and others).

This first course was a skunkworks project, which we did entirely on our own without any endorsement from ETH or any of the main MOOC players. We and our students have very much benefited from the consequent flexibility, and the use of homegrown technology relying on the MOODLE framework. We will keep this course for our own students and for any outside participant who prefers a small-scale, “boutique” version. But the EdX brand and EdX’s marketing power will enable us to reach a much broader audience. We want to provide the best introductory computing course on the market and the world needs to know about it. In addition, the full support of media services at ETH  helped us reach a higher standard on the technical side. (For our first course, the home-brewed one, we did not have a studio, so that every time an ambulance drove by — our offices are close to the main Zurich hospital — we had to restart the current take.)

The course’s content is not exactly the same: we have broadened the scope from just programming to computing, although it retains a strong programming component. We introduced additional elements such as an interview with Professor Peter Widmayer of ETH on the basics of computer science theory. For both new material and the topics retained from the first version we have adapted to the accepted MOOC practice of short segments, although we did not always exactly meet the eight-minute upper limit that was suggested to us.

We hope that you, and many newcomers, will like the course and benefit from it.

References

[3] EdX course: Computing: Art, Magic, Science, preview available here.

[2] Bertrand Meyer: Touch of Class: Learning how to Program Well, with Objects and Contracts, Springer Verlag, revised printing, 2013, book page here.

[3] Learning to Program, Online: article from this blog, 3 February 2014, available here.

For almost anyone programming in Eiffel, contracts are just a standard part of daily life; Patrice Chalin’s pioneering study of a few years ago [1] confirmed this impression. A larger empirical study is now available to understand how developers actually use contracts when available. The study, to published at FM 2014 [2] covers 21 programs, not just in Eiffel but also in JML and in Code Contracts for C#, totaling 830,000 lines of code, and following the program’s revision history for a grand total of 260 million lines of code over 7700 revisions. It analyzes in detail whether programmers use contracts, how they use them (in particular, which kinds, among preconditions, postconditions and invariants), how contracts evolve over time, and how inheritance interacts with contracts.

The paper is easy to read so I will refer you to it for the detailed conclusions, but one thing is clear: anyone who thinks contracts are for special development or special developers is completely off-track. In an environment supporting contracts, especially as a native part of the language, programmers understand their benefits and apply them as a matter of course.

References

[1] Patrice Chalin: Are practitioners writing contracts?, in Fault-Tolerant System, eds. Butler, Jones, Romanovsky, Troubitsyna, Springer LNCS, vol. 4157, pp. 100–113, 2006.

[2] H.-Christian Estler, Carlo A. Furia, Martin Nordio, Marco Piccioni and Bertrand Meyer: Contracts in Practice, to appear in proceedings of 19th International Symposium on Formal Methods (FM 2014), Singapore, May 2014, draft available here.

I have mentioned this paper before (see the earlier blog entry here) but it is now going to be published [1] and has been significantly revised, both to take referee comments into account and because we found better ways to present the concepts.

We have  endeavored to explain better than in the draft why the concept of negative variable is necessary and why the usual techniques for modeling object-oriented programs do not work properly for the fundamental OO operation, qualified call x.r (…). These techniques are based on substitution and are simply unable to express certain properties (let alone verify them). The affected properties are those involving properties of the calling context or the global project structure.

The basic idea (repeated in part from the earlier post) is as follows. In modeling OO programs, we have to take into account the unique “general relativity” property of OO programming: all the operations you write are expressed relative to a “current object” which changes repeatedly during execution. More precisely at the start of a call x.r (…) and for the duration of that call the current object changes to whatever x denotes — but to determine that object we must again interpret x in the context of the previous current object. This raises a challenge for reasoning about programs; for example in a routine the notation f.some_reference, if f is a formal argument, refers to objects in the context of the calling object, and we cannot apply standard rules of substitution as in the non-OO style of handling calls.

We introduced a notion of negative variable to deal with this issue. During the execution of a call x.r (…) the negation of x , written x’, represents a back pointer to the calling object; negative variables are characterized by axiomatic properties such as x.x’= Current and x’.(old x)= Current.

The paper explains why this concept is necessary, describes the associated formal rules, and presents applications.

Reference

[1] Bertrand Meyer and Alexander Kogtenkov: Negative Variables and the Essence of Object-Oriented Programming, to appear in Specification, Algebra, and Software, eds. Shusaku Iida, Jose Meseguer and Kazuhiro Ogata, Springer Lecture Notes in Computer Science, 2014, to appear. See text here.

In honor of Niklaus Wirth’s 80-th birthday we are organizing a symposium at ETH on February 20, 2014. This is a full-day event with invited talks by:

• Vint Cerf
• Hans Eberlé
• Michael Franz
• me
• Carroll Morgan
• Martin Odersky
• Clemens Szyperski
• Niklaus Wirth himself

From the symposium’s web page:

Niklaus Wirth was a Professor of Computer Science at ETH Zürich, Switzerland, from 1968 to 1999. His principal areas of contribution were programming languages and methodology, software engineering, and design of personal workstations. He designed the programming languages Algol W, Pascal, Modula-2, and Oberon, was involved in the methodologies of structured programming and stepwise refinement, and designed and built the workstations Lilith and Ceres. He published several text books for courses on programming, algorithms and data structures, and logical design of digital circuits. He has received various prizes and honorary doctorates, including the Turing Award, the IEEE Computer Pioneer, and the Award for outstanding contributions to Computer Science Education.

Participation is free (including breaks, lunch and the concluding “Apéro”) but space is strictly limited and we expect to run out of seats quickly. So if you are interested (but only if you are certain to attend) please register right away.

Symposium page and access to registration form: here.

For a while now I have  been engaged in  a core problem of software verification: the aliasing problem. As with many difficult problems in science, it is easy to state the basic question: can we determine automatically whether at a program point p the values of two reference expressions e and f can ever denote the same object?

Alias analysis lies at the core of many problems in software analysis and verification.

Earlier work [2] I introduced an “alias calculus”. The calculus is a set of rules, attached to the constructs of the programming language, to compute the “alias relation”: the set of possibly aliased expression pairs. A new paper [1] with Sergey Velder and Alexander Kogtenkov improves the model (correcting in particular an error in the axiom for assignment, whose new version has been proved sound using Coq) and applies it to the inference of frame properties. Here the abstract:

Alias analysis, which determines whether two expressions in a program may reference to the same object, has many potential applications in program construction and verification. We have developed a theory for alias analysis, the “alias calculus”, implemented its application to an object-oriented language, and integrated the result into a modern IDE. The calculus has a higher level of precision than many existing alias analysis techniques. One of the principal applications is to allow automatic change analysis, which leads to inferring “modifies clauses”, providing a significant advance towards addressing the Frame Problem. Experiments were able to infer the “modifies” clauses of an existing formally specied library. Other applications, in particular to concurrent programming, also appear possible. The article presents the calculus, the application to frame inference including experimental results, and other projected applications. The ongoing work includes building more efficient model capturing aliasing properties and soundness proof for its essential elements.

This is not the end of the work, as better models and implementations are needed, but an important step.

References

[1] Sergey Velder, Alexander Kogtenkovand Bertrand Meyer: Alias Calculus, Frame Calculus and Frame Inference, in Science of Computer Programming, to appear in 2014 (appeared online 26 November 2013); draft available here, published version here.
[2] Bertrand Meyer: Steps Towards a Theory and Calculus of Aliasing, in International Journal of Software and Informatics, Chinese Academy of Sciences, 2011, pages 77-116, available here.

I have mentioned this paper before but as a draft. It has now been accepted by ACM’s Computing Surveys and is scheduled to appear in September 2014; the current text, revised from the previous version, is available [1].

Here is the abstract:

Software verification has emerged as a key concern for ensuring the continued progress of information technology. Full verification generally requires, as a crucial step, equipping each loop with a “loop invariant”. Beyond their role in verification, loop invariants help program understanding by providing fundamental insights into the nature of algorithms. In practice, finding sound and useful invariants remains a challenge. Fortunately, many invariants seem intuitively to exhibit a common flavor. Understanding these fundamental invariant patterns could therefore provide help for understanding and verifying a large variety of programs.

We performed a systematic identification, validation, and classification of loop invariants over a range of fundamental algorithms from diverse areas of computer science. This article analyzes the patterns, as uncovered in this study,governing how invariants are derived from postconditions;it proposes a taxonomy of invariants according to these patterns, and presents its application to the algorithms reviewed. The discussion also shows the need for high-level specifications based on “domain theory”. It describes how the invariants and the corresponding algorithms have been mechanically verified using an automated program prover; the proof source files are available. The contributions also include suggestions for invariant inference and for model-based specification.

Reference

[1] Carlo Furia, Bertrand Meyer and Sergey Velder: Loop invariants: Analysis, Classification and Examples, in ACM Computing Surveys, to appear in September 2014, preliminary text available here.

The following presentations from our ETH group in the ICSE week (International Conference on Software Engineering, San Francisco) address important issues of software specification and verification, describing new techniques that we have recently developed as part of our work building EVE, the Eiffel Verification Environment. One is at ICSE proper and the other at VSTTE (Verified Software: Tools, Theories, Experiments). If you are around please attend them.

Julian Tschannen will present Program Checking With Less Hassle, written with Carlo A. Furia, Martin Nordio and me, at VSTTE on May 17 in the 15:30-16:30 session (see here in the VSTTE program. The draft is available here. I will write a blog article about this work in the coming days.

Nadia Polikarpova will present What Good Are Strong Specifications?, written with , Carlo A. Furia, Yu Pei, Yi Wei and me at ICSE on May 22 in the 13:30-15:30 session (see here in the ICSE program). The draft is available here. I wrote about this paper in an earlier post: see here. It describes the systematic application of theory-based modeling to the full specification and verification of advanced software.

The 2013 LASER summer school, organized by our chair at ETH, will take place September 8-14, once more in the idyllic setting of the Hotel del Golfo in Procchio, on the island of Elba in Italy. This is already the 10th conference; the roster of speakers so far reads like a who’s who of software engineering.

The theme this year is Software for the Cloud and Big Data and the speakers are Roger Barga from Microsoft, Karin Breitman from EMC,  Sebastian Burckhardt  from Microsoft,  Adrian Cockcroft from Netflix,  Carlo Ghezzi from Politecnico di Milano,  Anthony Joseph from Berkeley,  Pere Mato Vila from CERN and I.

LASER always has a strong practical bent, but this year it is particularly pronounced as you can see from the list of speakers and their affiliations. The topic is particularly timely: exploring the software aspects of game-changing developments currently redefining the IT scene.

The LASER formula is by now well-tuned: lectures over seven days (Sunday to Saturday), about five hours in the morning and three in the early evening, by world-class speakers; free time in the afternoon to enjoy the magnificent surroundings; 5-star accommodation and food in the best hotel of Elba, made affordable as we come towards the end of the season (and are valued long-term customers). The group picture below is from last year’s school.

Participants are from both industry and academia and have ample opportunities for interaction with the speakers, who typically attend each others’ lectures and engage in in-depth discussions. There is also time for some participant presentations; a free afternoon to discover Elba and brush up on your Napoleonic knowledge; and a boat trip on the final day.

Information about the 2013 school can be found here.

Lack of a precise context can render discussions of software engineering and particularly of software quality meaningless. Take for example the (usually absurd) statement “We cannot expect that programmers will equip their programs with contracts”. Whom do you mean? A physicist who writes 50 lines of Matlab code to produce a graph illustrating his latest experiment? A member of the maintenance team for Microsoft Word? A programmer on the team for a flight control system? These are completely different constituencies, and the answer is also different. In the last case, the answer is probably that we do not care what the programmers like and do not like. When you buy an electrical device that malfunctions, would you accept from the manufacturer the excuse that differential equations are, really, you see, too hard for our electrical engineers?

In discussing the evolution of software methods and tools we must first specify what and whom we are talking about. The following ABC characterization is sufficient for most cases.

C is for Casual. Programs in that category do all kinds of useful things, and like anything else they should work properly, but if they are not ideal in software engineering terms of reliability, reusability, extendibility and so on — if sometimes they crash, sometimes produce not-quite-right results,  cannot be easily understood or maintained by anyone other than their original developers, target just one platform, run too slowly, eat up too much memory, are not easy to change, include duplicated code — it is not the end of the world. I do not have any scientific figures, but I suspect that most of the world’s software is actually in that category, from JavaScript or Python code that runs web sites to spreadsheet macros. Obviously it has to be good enough to serve its needs, but “good enough” is good enough.

B is for Business. Programs in that category run key processes in the organization. While often far from impeccable, they must satisfy strict quality constraints; if they do not, the organization will suffer significantly.

A is for Acute. This is life-critical software: if it does not work — more precisely, if it does not work exactly right — someone will get killed, someone will lose huge amounts of money, or something else will go terribly wrong. We are talking transportation systems, software embedded in critical devices, make-or-break processes of an organization.

Even in a professional setting, and even within a single company, the three categories usually coexist. Take for example a large engineering or scientific organization.  Some programs are developed to support experiments or provide an answer to a specific technical question. Some programs run the organization, both on the information systems side (enterprise management) and on the technical side (large scientific simulations, experiment set-up). And some programs play a critical role in making strategy decisions, or run the organization’s products.

The ABC classification is independent of the traditional division between enterprise and technical computing. Organizations often handle these two categories separately, whereas in fact they raise issues of similar difficulty and are subject to solutions of a similar nature. It is more important to assess the criticality of each software projects, along the ABC scale.

It is surprising that few organizations make that scale explicit.  It is partly a consequence of that neglect that many software quality initiatives and company-wide software engineering policies are ineffective: they lump everything together, and since they tend to be driven by A-grade applications, for which the risk of bad quality is highest, they create a burden that can be too high for C- and even B-grade developments. People resent the constraints where they are not justified, and as a consequence ignore them where they would be critical. Whether your goal for the most demanding projects is to achieve CMMI qualification or to establish an effective agile process, you cannot impose the same rules on everyone. Sometimes the stakes are high; and sometimes a program is just a program.

The first step in establishing a successful software policy is to separate levels of criticality, and require every development to position itself along the resulting scale. The same observation qualifies just about any discussion of software methodology. Acute, Business or Casual: you must know your ABC.

In modeling object-oriented programs, for purposes of verification (proofs) or merely for a better understanding, we are faced with the unique “general relativity” property of OO programming: all the operations you write (excluding non-OO mechanisms such as static functions) are expressed relative to a “current object” which changes repeatedly during execution. More precisely at the start of a call x.r (…) and for the duration of that call the current object changes to whatever x denotes — but to determine that object we must again interpret x in the context of the previous current object. This raises a challenge for reasoning about programs; for example in a routine the notation f.some_reference, if f is a formal argument, refers to objects in the context of the calling object, and we cannot apply standard rules of substitution as in the non-OO style of handling calls.

In earlier work [1, 2] initially motivated by the development of the Alias Calculus, I introduced a notion of negative variable to deal with this issue. During the execution of a call x.r (…) the negation of x , written x’, represents a back pointer to the calling object; negative variables are characterized by axiomatic properties such as x.x’= Current and x’.(old x)= Current. Alexander Kogtenkov has implemented these ideas and refined them.

In a recent paper under submission [3], we review the concepts and applications of negative variables.

References

[1] Bertrand Meyer: Steps Towards a Theory and Calculus of Aliasing, in International Journal of Software and Informatics, 2011, available here.

[2] Bertrand Meyer: Towards a Calculus of Object Programs, in Patterns, Programming and Everything, Judith Bishop Festschrift, eds. Karin Breitman and Nigel Horspool, Springer-Verlag, 2012, pages 91-128, available here.

[3] Bertrand Meyer and Alexander Kogtenkov: Negative Variables and the Essence of Object-Oriented Programming, submitted for publication, 2012. [Updated 13 January 2014: I have removed the link to the draft mentioned in this post since it is now superseded by the new version, soon to be published, and available here.]

Actually it is not a musical but an extensive survey. I have long been fascinated by the notion of loop invariant, which describes the essence of a loop. Considering a loop without its invariant is like conducting an orchestra without a score.

In this submitted survey paper written with Sergey Velder and Carlo Furia [1], we study loop invariants in depth and describe many algorithms from diverse areas of computer science through their invariants. For simplicity and clarity, the specification technique uses the Domain Theory technique described in an earlier article on this blog [2] (see also [3]). The invariants were verified mechanically using Boogie, a sign of how much more realistic verification technology has become in recent years.

The survey was a major effort (we worked on it for a year and a half); it is not perfect but we hope it will prove useful in the understanding, teaching and verification of important algorithms.

Here is the article’s abstract:

At the heart of every loop, and hence of all significant algorithms, lies a loop invariant: a property ensured by the initialization and maintained by every iteration so that, when combined with the exit condition, it yields the loop’s final effect. Identifying the invariant of every loop is not only a required step for software verification, but also a key requirement for understanding the loop and the program to which it belongs. The systematic study of loop invariants of important algorithms can, as a consequence, yield insights into the nature of software.

We performed this study over a wide range of fundamental algorithms from diverse areas of computer science. We analyze the patterns according to which invariants are derived from postconditions, propose a classification of invariants according to these patterns, and present its application to the algorithms reviewed. The discussion also shows the need for high-level specification and invariants based on “domain theory”. The included invariants and the corresponding algorithms have been mechanically verified using an automatic program prover. Along with the classification and applications, the conclusions include suggestions for automatic invariant inference and general techniques for model-based specification.

References

[1] Carlo Furia, Bertrand Meyer and Sergey Velder: Loop invariants: analysis, classification, and examples, submitted for publication, December 2012, draft available here.

[2] Domain Theory: the Forgotten Step in Program Verification, article from this blog, 11 April 2012, available here.

[3] Domain Theory: Precedents, article from this blog, 11 April 2012, available here

Alexander Kogtenkov pointed out to me that precursor work to my papers on the Alias Calculus [1] [2] had been published by John Whaley and Martin Rinard [3]. There are some significant differences; in particular my rules are simpler, and their work is not explicitly presented as a calculus. But many of the basic ideas are the same. The reason I did not cite that paper is simply that I was not aware of it; I am happy to correct the omission.

References

[1] Bertrand Meyer: Towards a Theory and Calculus of Aliasing, in Journal of Object Technology, vol. 9, no. 2, March-April 2010, pages 37-74, available here (superseded by [2])
[2] Bertrand Meyer: Steps Towards a Theory and Calculus of Aliasing, in International Journal of Software and Informatics, 2011, available here (revised and improved version of [1].)
[3] John Whaley and Martin Rinard: Compositional Pointer and Escape Analysis for Java Programs, in POPL 1999, available here.

Both Gary Leavens and Jim Horning commented (partly here, partly on Facebook) about my Domain Theory article [1] to mention that Larch had mechanisms for domain modeling and specification reuse. As Horning writes:

The Larch Shared Language was really all about creating reusable domain theories, including theorems about the domains.  See, for example [2] and [3].

I am honored that they found the time to write about the article and happy to acknowledge Larch, one of the most extensive efforts, over several decades, to provide serious notations and tools for specification. Leavens’s and Horning’s messages gave me the opportunity to re-read some Larch papers and discover a couple I did not know.

My article did not try to provide exhaustive references; if it had, Larch would have been among them. I would probably have cited my own paper on M [4], earlier than [3], which introduces a notation for composing specifications; see section 1.4 (“Features of the M method and the associated notation have thus been devised to allow for modular descriptions of systems. A system description may include an interface paragraph that describes the connection of the current specification with others, existing or yet to be written”) and the  presentation of these mechanisms in section 5.

Larch traits, described in [3], pursue a similar aim, but the earlier article cited by Horning [2] is a general, informal discussion of formal specification; it does not mention traits, and in fact does not cite Larch, stating instead “We have experimented with the use of two very different tools, PIE and Affirm, in constructing modest sized algebraic specifications”. Its general observations about the specification task remain useful today, and it does mention reuse in passing.

If we were to look for precedents, the basic source would have to be the Clear specification language of Goguen and Burstall, for which the citations [5, 6, 7] all appear in my M paper [4] and go back further: 1977-1981. Clear made a convincing case for modularizing specifications, and defined supporting language constructs.

Since these early publications, many people have come to realize that reuse and composition can be as useful on the specification side as they are for programming. Typical specification and verification techniques, however, do not take advantage of this idea and tend to make us restart every time from the lowest level. Domain Theory, as outlined in [1], is intended to bring abstraction, which has proved so beneficial in other parts of software engineering, to the world of specification.

References

[1] Domain Theory: The Forgotten step in program verification, an article in this blog, see here.

[2] John V. Guttag, James J. Horning, Jeannette M. Wing: Some Notes on Putting Formal Specifications to Productive Use, in Science of Computer Programming, vol. 2, no. 1, 1982, pages 53-68. (BM note: I found a copy here.)

[3] John V. Guttag, James J. Horning: A Larch Shared Language Handbook, in Science of Computer Programming, vol. 6, no. 2, 1986, pages 135-157. (BM note: I found a copy here, which also has a link to the Larch report.)

[4] Bertrand Meyer: M: A System Description Method, Technical Report TR CS 85-15, University of California, Santa Barbara, 1985, available here.

[5] Rod M. Burstall and Joe A. Goguen: Putting Theories Together to Make Specifications, in Proceedings of 5th International Joint Conference on Artificial Intelligence, Cambridge (Mass.), 1977, pages 1045- 1058.

[6] Rod M. Burstall and Joe A. Goguen: “The Semantics of Clear, a Specification Language,” in Proceedings of Advanced Course on Abstract Software Specifications, Copenhagen, Lecture Notes on Computer Science 86, Copenhagen, Springer-Verlag, 1980, pages 292-332, available here.

[7] Rod M. Burstall and Joe A. Goguen: An Informal Introduction to Specifications using Clear, in The Correctness Problem in Computer Science, eds R. S. Boyer and JJ. S. Moore, Springer-Verlag, 1981, pages 185-213.