Bertrand Meyer's technology+ blog

I think I recently understood how software should be designed — or at least, since I have informally practiced the method for some time, how to explain it. Maybe not absolutely all types of software, but the most important kind: APIs (abstract program interfaces). The key task in software design is to define proper interfaces; if it is done right, everything else will fall into place, and if it is done wrong, there will be no end of problems everywhere else.

To put a Swiss theme to the description I may call this approach the Gotthard method. You are building a tunnel, starting from both sides at the same time, the northern, rainy, German-speaking part, and the southern, sunny, Italian-speaking part. (Actual languages and climates may vary.)

For the method to work it is really important that the two crews should meet somewhere in the middle:

In software design we are typically confronted with two views:

• The client view: application software needs certain abstractions and functionalities that will make it easy to produce clear, simple, extendible, reusable client programs.
• The supplier view: the necessary mechanisms are usually available in a raw form directly reflecting the underlying platform, a combination of hardware and software facilities.

Good design is a negotiation and iteration process that tries to reconcile the two views, working top-down from the client side and bottom-up from the supplier side, just as you would work when digging a tunnel between Unterwald and the Tessin.

As an example, consider a Web-oriented API. On the supplier side, we have a stateless protocol with essentially one mechanism: processing a request and sending a response. On the client side, we want to enable the building of applications, such as an e-commerce site, which need to pretend that they are working with stateful sessions, just as with a classical client-server GUI setup. The task of building software is to provide what the client application needs, in terms that make sense to the client and with all the abstractions that it needs — in our example, SESSION, STATE, USER and so on.

Since these higher-level abstractions are not directly provided by the supplier side, they need to be implemented or, to use a more appropriate term, faked. After all, everything in computer science is about faking: pretending that we have machines that we really don’t, simply by building them conceptually, in the form of APIs, in terms of machines that we have already built (bottom-up approach) or hope to build (top-down approach). “Building” a machine here means— except for the bottom-most machines, down at the level of the hardware, which very few programmers ever use directly anyway —faking them again, in terms of simpler ones. Fakes all the way down.

The process of software design then consists of developing intermediate levels of abstraction until we reach a compromise: a set of abstractions that satisfy the needs of application programmers and are efficiently implementable (or better yet, already implemented as part of this negotiation process) on the basis of what was available in the first place.

A poorly functioning software process will be more like yoyo design: trying something too abstract, then something too low-level and so on, converging too late if at all. Effective design is like boring a tunnel using modern engineering techniques, which rely on a clear understanding of where the crews start on both sides and make sure they end up meeting in the right place.

Photo reference: Herrenknecht AG, www.herrenknecht.com.

After a few weeks of use, Microsoft Outlook tends in my experience to go into a kind of thrashing mode where the user interface no longer quite functions as it should, although to the tool’s credit it does not lose information. Recently I have been getting pop-up warnings such as

A required resource was what? The message reminded me of an episode in a long-ago game of Scrabble, in which I proposed ADOABOUT as a word. “Ado about what? ”, the other players asked, and were not placated by my answer.

The message must have been trying to say  that a required resource was missing, or not found, but at the time of getting the final detail Outlook must have run out of UI resources and hence could not summon the needed text string. Not surprising, since running out of resources is precisely what caused the message to appear, in a valiant attempt to tell the user what is going on. (Valiant but not that useful: if you are not a programmer on the Outlook development team but just a customer trying to read email, it is not absolutely obvious how the message, even with the missing part, helps you.) The irony in the example is that the title bar suggests the problem arose in connection with trying to display the “Social Connector” area, a recent Outlook feature which I have never used. (Social connector? Wasn’t the deal about getting into computer science in the first place that for the rest of your life you’d be spared the nuisance of social connections? One can no longer trust anything nowadays.)

We can sympathize with whoever wrote the code. The Case Of The Resource That Was (Not) is an example of a general programming problem which we may call Space Between Your Back And Wall  or SBYBAW:  when you have your back against the wall, there is not much maneuvering space left.

A fairly difficult case of the SBYBAW problem arises in garbage collection, for example for object-oriented languages. A typical mark-and-sweep garbage collector must traverse the entire object structure to remove all the objects that have not been marked as reachable from the stack. The natural way to write a graph traversal algorithm is recursive: visit the roots; then recursively traverse their successors, flagging visited objects in some way to avoid cycling. Yes, but the implementation of a recursive routine relies on a stack of unpredictable size (the longest path length). If we got into  garbage collection, most likely it’s that we ran out of memory, precisely the kind of situation in which we cannot afford room for unpredictable stack growth.

In one of the early Eiffel garbage collectors, someone not aware of better techniques had actually written the traversal recursively; had the mistake not been caught early enough, it would no doubt have inflicted unbearable pain on humankind. Fortunately there is a solution: the Deutsch-Schorr-Waite algorithm [1], which avoids recursion on the program side by perverting the data structure to  replace some of the object links by recursion-control links; when the traversal’s execution proceeds along an edge, it reverses that edge to permit eventual return to the source. Strictly speaking, Deutsch-Schorr-Waite still requires a stack of booleans — to distinguish original edges from perverted ones — but we can avoid a separate stack (even just  a stack of booleans, which can be compactly represented in a few integers) by storing these booleans in the mark field of the objects themselves. The resulting traversal algorithm is a beauty — although it is fairly tricky, presents a challenge for verification tools, and raises new difficulties in a multi-threaded environment.

Deutsch-Schorr-Waite is a good example of “Small Memory Software” as studied in a useful book of the same title [2]. The need for Small Memory Software does not just arise for embedded programs running on small devices, but also in mainstream programming whenever we face the SBYBAW issue.

The SBYBAW lesson for the programmer is tough but simple. The resources we have at our disposal on a computing system may be huge, but they are always finite, and our programs’ appetite for resources will eventually exhaust them. At that stage, we have to deal with the SBYBAW rule, which sounds like a tautology but is an encouragement to look for clever algorithms:  techniques for freeing resources when no resources remain must not request new resources.

References

[1] Deutsch-Schorr-Waite is described in Knuth and also in [2]. Someone should start a Wikipedia entry.

[2] James Noble and Charles Weir: Small Memory Software: Patterns for Systems with Limited Memory, Addison-Wesley, 2001.

(With all dues to [1], but going up from four to five as it is good to be brief yet not curt.)

At the start there was Alan. He was the best of all: built the right math model (years ahead of the real thing in any shape, color or form); was able to prove that no one among us can know for sure if his or her loops — or their code as a whole — will ever stop; got to crack the Nazis’ codes; and in so doing kind of saved the world. Once the war was over he got to build his own CPUs, among the very first two or three of any sort. But after the Brits had used him, they hated him, let him down, broke him (for the sole crime that he was too gay for the time or at least for their taste), and soon he died.

There was Ed. Once upon a time he was Dutch, but one day he got on a plane and — voilà! — the next day he was a Texan. Yet he never got the twang. The first topic that had put him on  the map was the graph (how to find a path, as short as can be, from a start to a sink); he also wrote an Algol tool (the first I think to deal with all of Algol 60), and built an OS made of many a layer, which he named THE in honor of his alma mater [2]. He soon got known for his harsh views, spoke of the GOTO and its users in terms akin to libel, and wrote words, not at all kind, about BASIC and PL/I. All this he aired in the form of his famed “EWD”s, notes that he would xerox and send by post along the globe (there was no Web, no Net and no Email back then) to pals and foes alike. He could be kind, but often he stung. In work whose value will last more, he said that all we must care about is to prove our stuff right; or (to be more close to his own words) to build it so that it is sure to be right, and keep it so from start to end, the proof and the code going hand in hand. One of the keys, for him, was to use as a basis for ifs and loops the idea of a “guard”, which does imply that the very same code can in one case print a value A and in some other case print a value B, under the watch of an angel or a demon; but he said this does not have to be a cause for worry.

At about that time there was Wirth, whom some call Nick, and Hoare, whom all call Tony. (“Tony” is short for a list of no less than three long first names, which makes for a good quiz at a party of nerds — can you cite them all from rote?) Nick had a nice coda to Algol, which he named “W”; what came after Algol W was also much noted, but the onset of Unix and hence of C cast some shade over its later life. Tony too did much to help the field grow. Early on, he had shown a good way to sort an array real quick. Later he wrote that for every type of unit there must be an axiom or a rule, which gives it an exact sense and lets you know for sure what will hold after every run of your code. His fame also comes from work (based in part on Ed’s idea of the guard, noted above) on the topic of more than one run at once, a field that is very hot today as the law of Moore nears its end and every maker of chips has moved to  a mode where each wafer holds more than one — and often many — cores.

Dave (from the US, but then at work under the clime of the North) must not be left out of this list. In a paper pair, both from the same year and both much cited ever since,  he told the world that what we say about a piece of code must only be a part, often a very small part, of what we could say if we cared about every trait and every quirk. In other words, we must draw a clear line: on one side, what the rest of the code must know of that one piece; on the other, what it may avoid to know of it, and even not care about. Dave also spent much time to argue that our specs must not rely so much on logic, and more on a form of table.  In a later paper, short and sweet, he told us that it may not be so bad that you do not apply full rigor when you chart your road to code, as long as you can “fake” such rigor (his own word) after the fact.

Of UML, MDA and other such TLAs, the less be said, the more happy we all fare.

A big step came from the cold: not just one Norse but two, Ole-J (Dahl) and Kris, came up with the idea of the class; not just that, but all that makes the basis of what today we call “O-O”. For a long time few would heed their view, but then came Alan (Kay), Adele and their gang at PARC, who tied it all to the mouse and icons and menus and all the other cool stuff that makes up a good GUI. It still took a while, and a lot of hit and miss, but in the end O-O came to rule the world.

As to the math basis, it came in part from MIT — think Barb and John — and the idea, known as the ADT (not all TLAs are bad!), that a data type must be known at a high level, not from the nuts and bolts.

There also is a guy with a long first name (he hates it when they call him Bert) but a short last name. I feel a great urge to tell you all that he did, all that he does and all that he will do, but much of it uses long words that would seem hard to fit here; and he is, in any case, far too shy.

It is not all about code and we must not fail to note Barry (Boehm), Watts, Vic and all those to whom we owe that the human side (dear to Tom and Tim) also came to light. Barry has a great model that lets you find out, while it is not yet too late, how much your tasks will cost; its name fails me right now, but I think it is all in upper case.  At some point the agile guys — Kent (Beck) and so on — came in and said we had got it all wrong: we must work in pairs, set our goals to no more than a week away, stand up for a while at the start of each day (a feat known by the cool name of Scrum), and dump specs in favor of tests. Some of this, to be fair, is very much like what comes out of the less noble part of the male of the cow; but in truth not all of it is bad, and we must not yield to the urge to throw away the baby along with the water of the bath.

I could go on (and on, and on); who knows, I might even come back at some point and add to this. On the other hand I take it that by now you got the idea, and even on this last day of the week I have other work to do, so ciao.

Notes

[1] Al’s Famed Model Of the World, In Words Of Four Signs Or Fewer (not quite the exact title, but very close): find it on line here.

[2] If not quite his alma mater in the exact sense of the term, at least the place where he had a post at the time. (If we can trust this entry, his true alma mater would have been Leyde, but he did not stay long.)

..

If I’m not pure, at least my jewels are [1].

..

We often need to be reassured that a routine, usually a function, is “pure”, meaning that it does not change the state of the computation. For example, a function used in a contract element (precondition, postcondition, class invariant, loop invariant) should be purely descriptive, since it is a specification element; evaluating it, typically for testing and debugging, should not create a change of behavior — a “Heisenberg effect” — in the very computation that it is intended to assess. Another application is in a concurrency context, particularly in SCOOP (see earlier posts and forthcoming ones): if one or more functions are pure, several of their executions can run  concurrently on the same object.

The notion of purity admits variants. The usual notion is what  [2] calls weak purity, which precludes changes to previously existing objects but allow creating new objects. In the EiffelBase library we also encounter routines that have another form of purity, which we may call “relative” purity: they can leave the same state on exit as they found on entry, but in-between they might change the state.  For the rest of this discussion we will rely on the standard notion of weak purity: no changes permitted on existing objects.

It is often suggested that the programming language should support specifying that a routine is pure; many people have indeed proposed the addition of a keyword such as pure to Eiffel. One of the reasons this is not — in my opinion — such a great idea is that purity is just a special case of the more general problem of framing: specifying and verifying what a routine does not change. If we can specify an arbitrary frame property, then we can, as a special case covered by the general mechanism, specify that a routine changes nothing.

To see why framing is so important, consider a class ACCOUNT with a routine deposit that has the postcondition

balance = old balance + sum………..— Where sum is the argument of deposit

Framing here means stating that nothing else than balance changes; for example the account’s owner and its number should remain the same. It is not practical to write all individual postcondition clauses such as

owner= old owner
number= old number

and so on. But we do need to specify these properties and enforce them, if only to avoid that a descendant class (maybe MAFIA_ACCOUNT) distort the rules defined by the original.

One technique is to add a so-called “modifies clause”, introduced by verification tools such as ESC-Java [3] and JML [4]. Modifies clauses raise some theoretical issues; in particular, the list of modified expressions is often infinite, so we must restrict ourselves to an abstract-data-type view where we characterize a class by commands and queries and the modifies clause only involves queries of the class. Many people find this hard to accept at first, since anything that is not talked about can change, but it is the right approach. A modifies clause of sorts, included in the postcondition, appeared in an earlier iteration of the Eiffel specification, with the keyword only (which is indeed preferable to modifies, which in the Eiffel style favoring grammatically simple keywords would be modify, since what we want to express is not that the routine must change anything at all  but that it may only change certain specified results!). The convention worked well with inheritance, since it included the rule that a clause such as only balance, in class  ACCOUNT, prescribes that the routine may not, in its modifies version as well as in any version redefined in descendants, change any other query known at the level of ACCOUNT; but a descendant version may change, subject to its own ACCOUNT clauses, any new query introduced by a descendant.

To declare a routine as pure, it would suffice to use an empty only clause (not very elegant syntactically — “only” what? — but one can get used to it).

This construct has been discarded, as it places too heavy a burden on the programmer-specifier. Here the key observation resulted from a non-scientific but pretty extensive survey I made of all the JML code I could get my hands on. I found that every time a query appeared in a modifies clause it was also listed in the postcondition! On reflection, this seems reasonable: if you are serious about specification, as anyone bothering to write such a clause surely is, you will not just express that something changes and stop there; you will write something about how it may change. Not necessarily the exact result, as in

my_query = precise_final_value

but at least some property of that result, as in

some_property (my_query)

This observation has, however, an inescapable consequence for language design: modifies or only clauses should be inferred by the compiler from the postcondition, not imposed on the programmer as an extra burden. The convention, which we may call the Implicit Framing Rule, is simple:

A routine may change the value of a query only if the query is specified in the routine’s postcondition

(or, if you like double negation, “no routine may change the value of a query other than those specified in its postcondition”). Here we say that a feature is “specified” in a postcondition if it appears there outside of the scope of an old expression. (Clearly, an occurrence such as old balance does not imply that balance can be modified, hence this restriction to occurrences outside of an old.)

With this convention the only clause becomes implicit: it would simply list all the queries specified in the postcondition, so there is no need for the programmer to write it. For the rare case of wanting to specify that a query q may change, but not wanting to specify how, it is easy to provide a library function, say involved, that always return true and can be used in postconditions, as in involved (q).

The convention is of course not just a matter of programming methodology but, in an IDE supporting verification, such as the EVE “Verification As a Matter Of Course” environment which we are building for Eiffel [5], the compiler will enforce the definition above — no change permitted to anything not specified in the postcondition — and produce an error in case of a violation. This also means that we can easily specify that a routine is pure: it must simply not specify any query in its postcondition. It may still list it in an old clause, as happens often in practice, e.g.

Result = old balance – Minimum_balance………..— In the postcondition of a function available_funds

Note the need to use old here. Apart from this addition of old to some postconditions, a considerable advantage of the convention is that most existing code using pure functions will be suitable to the new purity enforcement without any need to provide new annotations.

I believe that this is the only sustainable convention. It does not, of course, solve the frame problem by itself (for attempts in this direction see [6, 7]), but it is a necessary condition for a solution that is simple, easily taught, fairly easily implemented, and effective. It goes well with model-based specifications [8, 9], which I believe are the technique of most promise for usable  specifications of object-oriented software. And it provides a straightforward, no-frills way to enforce purity where prescribed by the Command-Query Separation principle [10, 11]: if I’m not pure, at least my functions must be.

References

[1] From the lyrics of the aria Glitter and Be Gay in Leonard Bernstein’s Candide, text by Lillian Hellman and others. Youtube offers several performances, including  by Diana Damrau (here) and Natalie Dessay (here) . For the text see e.g. here.

[2] Adam Darvas and Peter Müller: Reasoning About Method Calls in Interface Specifications, in Journal of Object Technology, Volume 5, no. 5, jUNE 2006, pages 59-85, doi:10.5381/jot.2006.5.5.a3, available here.

[3] C. Flanagan, K.R.M. Leino, M. Lillibridge, G. Nelson, J. B. Saxe and R. Stata: Extended static checking for Java, in PLDI 2002 (Programming Language Design and Implementation), pages 234–245, 2002.

[4] Gary Leavens et al.: Java Modeling Language, see references here.

[5] Julian Tschannen, Carlo A. Furia, Martin Nordio, and Bertrand Meyer: Verifying Eiffel Programs with Boogie, to appear in Boogie 2011, First International Workshop on Intermediate Verification Languages, Wroclaw, August 2011. See documentation about the EVE project on the project page.

[6] Ioannis Kassios: Dynamic Frames: Support for Framing, Dependencies and Sharing Without Restrictions, in Formal Methods 2006, eds. J. Misra, T. Nipkow and E. Sekerinski, Lecture Notes in Computer Science 4085, Springer Verlag, 2006, pages 268-283.

[7] Bernd Schoeller: Making Classes Provable through Contracts, Models and Frames, PhD thesis, ETH Zurich, 2007, available here

[8] Bernd Schoeller, Tobias Widmer and Bertrand Meyer: Making Specifications Complete Through Models, in Architecting Systems with Trustworthy Components, eds. Ralf Reussner, Judith Stafford and Clemens Szyperski, Lecture Notes in Computer Science, Springer-Verlag, 2006, available here.

[9] Nadia Polikarpova, Carlo Furia and Bertrand Meyer: Specifying Reusable Components, in Verified Software: Theories, Tools, Experiments (VSTTE ’10), Edinburgh, UK, 16-19 August 2010, Lecture Notes in Computer Science, Springer Verlag, 2010, available here.

[10] Bertrand Meyer: Object-Oriented Software Construction, first (1988) and second (1997) editions, Prentice Hall.

[11] Bertrand Meyer: Touch of Class: An Introduction to Programming Well, Using Objects and Contracts, Springer Verlag, 2009.

It was a bit imprudent last Monday to announce the continuation of the SCOOP discussion for this week; with the TOOLS conference happening now, with many satellite events such as the Eiffel Design Feast of the past week-end and today’s “New Eiffel Technology Community” workshop, there is not enough time for a full article. Next week might also be problematic. The SCOOP series will resume, but in the meantime I will report on other matters.

As something that can be conveniently typed in while sitting in the back of the TOOLS room during fascinating presentations, here is a bit of publicity for the next round of one-day seminars for industry — “Compact Course” is the official terminology — that I will be teaching at ETH in Zurich next November (one in October), some of them with colleagues. It’s the most extensive session that we have ever done; you can see the full programs and registration information here.

• Software Engineering for Outsourced and Distributed Development, 27 October 2011
  Taught with Peter Kolb and Martin Nordio

• Requirements Engineering, 17 November

• Software Testing and Verification: state of the art, 18 November
  With Carlo Furia and Sebastian Nanz

• Agile Methods: the Good, the Bad and the Ugly, 23 November

• Concepts and Constructs of Concurrent Computation, 24 November
  With Sebastian Nanz

• Design by Contract, 25 November

The agile methods course is new; its summary reads almost like a little blog article, so here it is.

Agile methods: the Good, the Bad and the Ugly

Agile methods are wonderful. They’ll give you software in no time at all, turn your customers and users into friends, catch bugs before they catch you, change the world, and boost your love life. Do you believe these claims (even excluding the last two)? It’s really difficult to form an informed opinion, since most of the presentations of eXtreme Programming and other agile practices are intended to promote them (and the consultants to whom they provide a living), not to deliver an objective assessment.

If you are looking for a guru-style initiation to the agile religion, this is not the course for you. What it does is to describe in detail the corpus of techniques covered by the “agile” umbrella (so that you can apply them effectively to your developments), and assess their contribution to software engineering. It is neither “for” nor “against” agile methods but fundamentally descriptive, pedagogical, objective and practical. The truth is that agile methods include some demonstrably good ideas along with some whose benefits are at best dubious. In addition (and this should not be a surprise) they cannot make the fundamental laws of software engineering go away.

Agile methods have now been around for more than a decade, during which many research teams, applying proven methods of experimental science, have performed credible empirical studies of how well the methods really work and how they compare to more traditional software engineering practices. This important body of research results, although not widely known, is critical to managers and developers in industry for deciding whether and how to use agile development. The course surveys these results, emphasizing the ones most directly relevant to practitioners.

A short discussion session will enable participants with experience in agile methods to share their results.

Taking this course will give you a strong understanding of agile development, and a clear view of when, where and how to apply them.

Schedule

Morning session: A presentation of agile methods

• eXtreme Programming, pair programming, Scrum, Test-Driven Development, continuous integration, refactoring, stakeholder involvement, feature-driven development etc.
• The agile lifecycle.
• Variants: lean programming etc.

Afternoon session (I): Assessment of agile methods

• The empirical software engineering literature: review of available studies. Assessment of their value. Principles of empirical software engineering.
• Agile methods under the scrutiny of empirical research: what helps, what harms, and what has no effect? How do agile methods fare against traditional techniques?
• Examples: pair programming versus code reviews; tests versus specifications; iterative development versus “Big Upfront Everything”.

Afternoon session (II): Discussion and conclusion

This final part of the course will present, after a discussion session involving participants with experience in agile methods, a summary of the contribution of agile methods to software engineering.

It will conclude with advice for organizations involved in software development and interested in applying agile methods in their own environment.

Target groups

CIOs; software project leaders; software developers; software testers and QA engineers.

EiffelStudio 6.8, released last month, contains the first official implementation of the SCOOP programming model for concurrent programming. This is an important milestone; let me try to explain why.

Concurrency challenging us

Concurrency is the principal stumbling block in the progress of programming. Do not take just my word for it:

• Intel: “Multi-core processing is taking the industry on a fast-moving and exciting ride into profoundly new territory. The defining paradigm in computing performance has shifted inexorably from raw clock speed to parallel operations and energy efficiency” [1].
• Rick Rashid (head of Microsoft Research):  “Multicore processors represent one of the largest technology transitions in the computing industry today, with deep implications for how we develop software.” [2].
• Bill Gates: “Multicore: This is the one which will have the biggest impact on us. We have never had a problem to solve like this. A breakthrough is needed in how applications are done on multicore devices.” [3]
• David Patterson: “Industry has basically thrown a Hail Mary. The whole industry is betting on parallel computing. They’ve thrown it, but the big problem is catching it.” [4]
• Gordon Bell: “I’m skeptical until I see something that gives me some hope…  the machines are here and we haven’t got it right.” [4].

What has happened? Concurrency  used to be a highly specialized domain of interest to a small minority of programmers building operating systems and networking systems and database engines. Just about everyone else could live comfortably pretending that the world was sequential. And then suddenly we all need to be aware of concurrency. The principal reason is the end of Moore’s law as we know it [5].

This chart show that we can no longer rely on the automatic and regular improvement to our programs’ performance, roughly by a factor of two every two years, thanks to faster chips. The free lunch is over; continued performance increases require taking advantage of concurrency, in particular through multithreading.

Performance is not the only reason for getting into concurrency. Another one is user convenience: ever since the first browser showed that one could write an email and load a Web page in the same window, users have been clamoring for multithreaded applications. Yet another source of concurrency requirements is the need to produce Internet and Web applications.

How do programmers write these applications? The almost universal answer relies on threading mechanisms, typically offered through some combination of language and library mechanisms: Java Threads, .NET threading, POSIX threads, EiffelThreads. The underlying techniques are semaphores and mutexes: nineteen-sixties vintage concepts, rife with risks of data races (access conflicts to a variable or resource, leading to crashes or incorrect computations) and deadlocks (where the system hangs). These risks are worse than the classical bugs of sequential programs because they are very difficult to detect through testing.

Ways to tame the beast

Because the need is so critical, the race is on — a “frantic” race in the words of a memorable New York Times article by John Markoff [4] — to devise a modern programming framework that will bring concurrent programming under control. SCOOP is a contender in this battle. In this post and the next I will try to explain why we think it is exactly what the world needs to tame concurrency.

The usual view, from which SCOOP departs, is that concurrent programming is intrinsically hard and requires a fundamental change in the way programmers think. Indeed some of the other approaches that have attracted attention imply radical departures from accepted programming paradigm:

• Concurrency calculi such as CSP [6, 7], CCS [8] and the π-Calculus [9] define  high-level mathematical frameworks addressing concurrency, but they are very far from the practical concerns of programmers. An even more serious problem is that they focus on only some aspects of programming, but being concurrent is only one property of a program, among many others (needing a database, relying on graphical user interface, using certain data structures, perform certain computations…). We need mechanisms that integrate concurrency with all the other mechanisms that a program uses.
• Functional programming languages have also offered interesting idioms for concurrency, taking advantage of the non-imperative nature of functional programming. Advocacy papers have argued for Haskell [10 and Erlang [11] in this role. But should the world renounce other advances of modern software engineering, in particular object-oriented programming, for the sake of these mechanisms? Few people are prepared to take that step, and (as I have discussed in a detailed article [12]) the advantages of functional programming are counter-balanced by the superiority of the object-oriented model in its support for the modular construction of realistic systems.

What if we did not have to throw away everything and relearn programming from the ground up for concurrency? What if we could retain the benefits of five decades of software progress, as crystallized in modern object-oriented programming? This is the conjecture behind SCOOP: that we can benefit from all the techniques we have learned to make our software reliable, extendible and reusable, and add concurrency to the picture in an incremental way.

From sequential to concurrent

A detailed presentation of SCOOP will be for next Monday, but let me give you a hint and I hope whet your appetite by describing how to move a typical example from sequential to concurrent. Here is a routine for transferring money between two accounts:

transfer (amount: INTEGER ; source, target: ACCOUNT)
               -- Transfer amount dollars from source to target.
        require
               enough: source·balance >= amount
        do
         source·withdraw (amount)
         target·deposit (amount)
        ensure
               removed: source·balance = old source·balance – amount
               added: target·balance = old target·balance + amount
        end

The caller must satisfy the precondition, requiring the source account to have enough money to withdraw the requested amount; the postcondition states that the source account will then be debited, and the target account credited, by that amount.

Now assume that we naïvely apply this routine in a concurrent context, with concurrent calls

        if acc1·balance >= 100 then transfer (acc1, acc2, 100) end

and

        if acc1·balance >= 100 then transfer (acc1, acc3, 100) end

If the original balance on acc1 is 100, it would be perfectly possible in the absence of a proper concurrency mechanism that both calls, as they reach the test acc1·balance >= 100, find the property to be true and proceed to do the transfer — but incorrectly since they cannot both happen without bringing the balance of acc1 below zero, a situation that the precondition of transfer and the tests were precisely designed to rule out. This is the classic data race. To avoid it in the traditional approaches, you need complicated and error-prone applications of semaphores or conditional critical regions (the latter with their “wait-and-signal” mechanism, just as clumsy and low-level as the operations on semaphores).

In SCOOP, such data races, and data races of any other kind, cannot occur. If the various objects involved are to run in separate threads of control, the declaration of the routine will be of the form

transfer (amount: INTEGER ; source, target: separate ACCOUNT)
               -- The rest of the routine exactly as before.

where separate is the only specific language keyword of SCOOP. This addition of the separate marker does the trick. will result in the following behavior:

• Every call to transfer is guaranteed exclusive access to both separate arguments (the two accounts).
• This simultaneous reservation of multiple objects (a particularly tricky task when programmers must take care of it through their own programs, as they must in traditional approaches) is automatically guaranteed by the SCOOP scheduler. The calls wait as needed.
• As a consequence, the conditional instructions (if … then… ) are no longer needed. Just call transfer and rely on SCOOP to do the synchronization and guarantee correctness.
• As part of this correctness guarantee, the calls may have to wait until the preconditions hold, in other words until there is enough money on the account.

This is the desired behavior in the transition from sequential to concurrent. It is achieved here not by peppering the code with low-level concurrent operations, not by moving to a completely different programming scheme, but by simply declaring which objects are “separate” (potentially running elsewhere.

The idea of SCOOP is indeed that we reuse all that we have come to enjoy in modern object-oriented programming, and simply declare what needs to be parallel, expecting things to work (“principle of least surprise”).

This is not how most of the world sees concurrency. It’s supposed to be hard. Indeed it is; very hard, in fact. But the view of the people who built SCOOP is that as much of the difficulty should be for the implementers. Hence the title of this article: for programmers, concurrency should be easy. And we think SCOOP demonstrates that it can be.

SCOOP in practice

A few words of caution: we are not saying that SCOOP as provided in EiffelStudio 6.8 is the last word. (Otherwise it would be called 7.0.) In fact, precisely because implementation is very hard, a number of details are still not properly handled; for example, as discussed in recent exchanges on the EiffelStudio user group [13], just printing out the contents of a separate string is non-trivial. We are working to provide all the machinery that will make everything work well, the ambitious goals and the practical details. But the basics of the mechanism are there, with a solid implementation designed to scale properly for large applications and in distributed settings.

In next week’s article I will describe in a bit more detail what makes up the SCOOP mechanisms. To get a preview, you are welcome to look at the documentation [14, 15]; I hope it will convince you that despite what everyone else says concurrent programming can be easy.

References

[1] Official Intel statement, see e.g. here.

[2] Rich Rashid, Microsoft Faculty Summit, 2008.

[3] This statement was cited at the Microsoft Faculty Summit in 2008 and is part of the official transcript; hence it can be assumed to be authentic, although I do not know the original source.

[4] Patterson and Bell citations from John Markoff, Faster Chips Are Leaving Programmers in Their Dust, New York Times, 17 December 2007, available here.

[5] The chart is from the course material of Tryggve Fossum at the LASER summer school in 2008.

[6] C.A.R. Hoare: em>Communicating Sequential Processes, Prentice Hall, 1985, also available online.

[7] Bill Roscoe: The Theory and Practice of Concurrency, revised edition, Prentice Hall, 2005, also available online.

[8] Robin Milner: Communication and Concurrency, Prentice Hall, 1989.

[9] Robin Milner: Communicating and Mobile Systems: The π-calculus, Cambridge University Press, 1999.

[10] Simon Peyton-Jones: Beautiful Concurrency, in Beautiful Code, ed. Greg Wilson, O’Reilly, 2007, also available online.

[11] Joe Armstrong: Erlang, in Communications of the ACM, vol. 53, no. 9, September 2010, pages 68-75.

[12] Bertrand Meyer: Software Architecture: Functional vs. Object-Oriented Design, in Beautiful Architecture, eds. Diomidis Spinellis and Georgios Gousios, O’Reilly, 2009, pages 315-348, available online.

[13] EiffelStudio user group; see here for a link to current discussions and to join the group.

[14] SCOOP project documentation at ETH, available here.

By describing a  poorly conceived hypothetical experiment, last week’s article described the “Professor Smith syndrome” consisting of four risks that threaten the validity of empirical software engineering experiments relying on students in a course:

• Professor Smith Risk 1: possible bias if the evaluator has a stake in the ideas or tools under assessment.
• Professor Smith Risk 2: creating different levels of motivation in the different groups (Hawthorne effect).
• Professor Smith Risk 3: extrapolating from students to professionals.
• Professor Smith Risk 4: violation of educational ethics if the experiment may cause some students to learn better than others.

If you have developed a great new method or tool and would like to assess it, the best way to address Risk 1 is to find someone else to do the assessment. What if  this solution is not practical? Recently we wanted to get some empirical evidence on the merits of the SCOOP (Simple Concurrent Object-Oriented Programming) approach to concurrency [1, 2], on which I have worked for a long time and which is now part of EiffelStudio since the release of 6.8 a couple of weeks ago. We wanted to see if, despite the Professor Smith risks, we could do a credible study ourselves.

The ETH Software Architecture course[3], into which we introduced some introductory material on concurrency last year (as part of a general effort to push more concurrency into software courses at ETH), looked like a good place to try an evaluation; it is a second-year course, where students, or so we thought, would have little prior experience in concurrent software design.

The study’s authors — Sebastian Nanz, Faraz Torshizi and Michela Pedroni — paid special attention to the methodological issues. To judge for yourself whether we addressed them properly, you can read the current version of our paper to be presented at ESEM 2011 [4]. Do note that it is a draft and that we will improve the paper for final publication.

Here is some of what we did. I will not address the Professor Smith Risk 3, the use of students, which (as Lionel Briand has pointed out in a comment on the previous article) published work has studied; in a later article I will give  references to some of that work. But we were determined to tackle the other risks explicitly, so as to obtain credible results.

The basic experiment was a session in which the students were exposed to two different design methods for concurrent software: multithreaded programming in Java, which I’ll call “Java Threads”, and SCOOP. We wanted to explore whether it is easier to program in SCOOP than in Java. This is too general a hypothesis, so it was refined into three concrete hypotheses: is it easier to understand a SCOOP program? Is it easier to find errors in SCOOP programs? Do programmers using SCOOP make fewer errors?

A first step towards reducing the effect — Professor Smith Risk 1 — of any emotional attachment of the experimenters  to one of the approaches, SCOOP in our case, was to generalize the study. Although what directly interested us was to compare SCOOP against Java Threads, we designed the study as a general scheme to compare concurrency approaches; SCOOP and Java Threads are just an illustration, but anyone else interested in assessing concurrency techniques — say Erlang versus C# concurrency — can apply the same methodology. This decision had two benefits: it freed the study from dependency on the particular techniques, hence, we hope, reducing bias; and as side attraction of the kind that is hard for researchers to resist, it increased the publishability of the results.

Circumstances unexpectedly afforded us another protection against any for-SCOOP bias: unbeknownst to us at the time of the study’s design, a first-year course had newly added (in 2009, whereas our study was performed in 2010) an introduction to concurrent programming — using Java Threads! While we had thought that concurrency in any form would be new to most students, in fact almost all of them had now seen Java Threads before. (The new material in the first-year course was taken by ETH students only, but many transfer students had also already had an exposure to Java Threads.) On the other hand, students had not had any prior introduction to SCOOP. So any advantage that one of the approaches may have had because of students’ prior experience would work against our hypotheses. This unexpected development would not help if the study’s results heavily favored Java Threads, but if they favored SCOOP it would reinforce their credibility.

A particular pedagogical decision was made regarding the teaching of our concurrency material: it started with a self-study rather than a traditional lecture. One of the reasons for this decision was purely pedagogical: we felt (and the course evaluations confirmed) that at that stage of the semester the students would enjoy a break in the rhythm of the course. But another reason was to avoid any bias that might have arisen from any difference in the lecturers’ levels of enthusiasm and effectiveness in teaching the two approaches. In the first course session devoted to concurrency, students were handed study materials presenting Java Threads and SCOOP and containing a test to be taken; the study’s results are entirely based on their answers to these tests. The second session was a traditional lecture presenting both approaches again and comparing them. The purpose of this lecture was to make sure the students got the full picture with the benefit of a teacher’s verbal explanations.

The study material was written carefully and with a tone as descriptive and neutral as possible. To make comparisons meaningful, it does not follow a structure specific to Java Threads or  SCOOP  (as we might have used had we taught only one of these approaches); instead it relies in both cases on the same overall plan  (figure 2 of the paper), based on a neutral analysis of concurrency concepts and issues: threads, mutual exclusion, deadlock etc. Each section then presents, for one such general concurrency question, the solution proposed by Java Threads or SCOOP.

This self-study material, as well as everything else about the study, is freely available on the Web; see the paper for the links.

In the self-study, all students studied both the Java Threads and SCOOP materials. They were randomly assigned to two groups, for which the only difference was the order of studying the approaches. We feel that this decision addresses the ethical issue (Professor Smith Risk 4): any pedagogical effect of reading about A before B rather than the reverse, in the course of a few hours, has to be minimal if you end up reading about the two of them, and on the next day follow a lecture that also covers both.

Having all students study both approaches — a crossover approach in the terminology of [5] — should also address the Hawthorne effect (Professor Smith Risk 2): students have no particular incentive to feel that one of the approaches is more hip than the other. While they are not told that SCOOP is partly the work of the instructors, some of them may know or guess this information; the consequences, positive or negative, are limited, since they are asked in both cases to do as well as they can in answering the assessment questions.

The design of that evaluation is another crucial element in trying to avoid bias. We tried, to the extent possible, to base the assessment on objective criteria. For the first hypothesis (program understanding) the technique was to ask the students to predict the output of some simple concurrent programs. To address the risk of a binary correct/incorrect assessment, and get a more fine-grained view, we devised the programs so that they would produce output strings and measured the Levenshtein (edit) distance to the correct result. For the second hypothesis (ease of program debugging), we gave students programs exhibiting typical errors in both approaches and asked them to tell us both the line number of any error they found and an explanation. Assessing the explanation required human analysis; the idea of also assigning partial credit for pointing out a line number without providing a good explanation is that it may be meaningful that a student found that something is amiss even without being quite able to define what it is. The procedure for the third hypothesis (producing programs with fewer errors) was more complex and required two passes over the result; it requires some human analysis, as you will see in the article, but we hope that the two-pass process removes any bias.

This description of the study is only partial and you should read the article [4] for the full details of the procedure.

So what did we find in the end? Does SCOOP really makes concurrency easier to learn, concurrent programs easier to debug, and concurrent programmers less error-prone? Here too  I will refer you to the article. Let me simply mention that the results held some surprises.

In obtaining these results we tried very hard to address the Professor Smith syndrome and its four risks. Since all of our materials, procedures and data are publicly accessible, described in some detail in the paper, you can determine for yourself how well we met this objective, and whether it is possible to perform credible assessments even of one’s own work.

References

Further reading: for general guidelines on how to conduct empirical research see [5]; for ethical guidelines, applied to psychological research but generalizable, see [6].

[1] SCOOP Eiffel documentation, available here.

[2] SCOOP project documentation at ETH, available here.

[3] Software Architecture course at ETH, course page (2011).

[4] Sebastian Nanz, Faraz Torshizi, Michela Pedroni and Bertrand Meyer: Design of an Empirical Study for Comparing the Usability of Concurrent Programming Languages, to appear in ESEM 2011 (ACM/IEEE International Symposium on Empirical Software Engineering and Measurement), 22-23 September 2011. Draft available here.

[5] Barbara A. Kitchenham, Shari L. Pfleeger, Lesley M. Pickard, Peter W. Jones, David C. Hoaglin, Khaled El-Emam and Jarrett Rosenberg: Preliminary Guidelines for Empirical Research in Software Engineering, national Research Council Canada (NRC-CNRC), Report ERB-1082, 2001, available here.

[6] Robert Rosenthal: Science and ethics in conducting, analyzing, and reporting psychological research, in  Psychological Science, 5, 1994, p127-134. I found a copy cached by a search engine here.

As stated in the Quiz of a few days ago (“Part 1 ”), we consider the following hypothetical report in experimental software engineering ([1], [2]):

Professor Smith has developed a new programming technique, “Suspect-Oriented Programming” (SOP). To evaluate SOP, he directs half of the students in his “Software Methodology” class to do the project using traditional techniques, and the others to use SOP.

He finds that projects by the students using SOP have, on the average, 15% fewer bugs than the others, and reports that SOP increases software reliability.

What’s wrong with this story?

Professor Smith’s attempt at empirical software engineering is problematic for at least four reasons. Others could arise, but we do not need to consider them if Professor Smith has applied the expected precautions: the number of students should be large enough (standard statistical theory will tell us how much to trust the result for various sample sizes); the students should be assigned to one of the two groups on a truly random basis; the problem should be amenable to both SOP and non-SOP techniques; and the assessment of the number of bugs should in the results should be based on fair and if possible automated evaluation. Some respondents to the quiz cited these problems, but they would apply to any empirical study and we can assume they are being taken care of.

The first problem to consider is that the evaluator and the author of the concept under evaluation are the same person. This is an approach fraught with danger. We have no reason to doubt Professor Smith’s integrity, but he is human. Deep down, he wants SOP to be better than the alternative. That is bound to affect the study. It would be much more credible if someone else, with no personal stake in SOP, had performed it.

The second problem mirrors the first on the students’ side. The students from group 1 were told that they used Professor Smith’s great idea, those from group 2 that they had to use old, conventional, boring stuff. Did both groups apply the same zeal to their work? After all, the students know that Professor Smith created SOP, and maybe he is an convincing advocate, so group 1 students will (consciously or not) do their best; those from group 2 have less incentive to go the extra mile. What we may have at play here is a phenomenon known as the Hawthorne effect [3]: if you know you are being tested for a new technique, you typically work harder and better — and may produce better results even if the technique is worthless! Experiments dedicated to studying this effect show that even  a group that is in reality using the same technique as another does better, at least at the beginning, if it is told that it is using a new, sexy technique.

The first and second problems arise in all empirical studies, software-related or not. They are the reason why medical experiments use placebos and double-blind techniques (where neither the subjects nor the experimenters themselves know who is using which variant). These techniques often do not directly transpose to software experiments, but we should all the same be careful about empirical studies of assessments of one’s own work and about possible Hawthorne effects.

The third problem, less critical, is the validity of a study relying on students. To what extent can we extrapolate from the results to a situation in industry? Software engineering students are on their way to becoming software professionals, but they are not professionals yet. This is a difficult issue because universities, rather than industry, are usually and understandably the place where experiments take place, an sometimes there is no other choice than using students. But then one can question the validity of the results. It depends on the nature of the questions being asked: if the question under study is whether a certain idea is easy to learn, using students is reasonable. But if it is, for example, whether a technique produces less buggy programs, the results can depend significantly on the subjects’ experience, which is different for students and professionals.

The last problem does not by itself affect the validity of the results, but it is a show-stopper nonetheless: Professor Smith’s experiment is unethical! If is is indeed true that SOP is better than the alternative, he is harming students from group 2; in the reverse case, he is harming students from group 1. Only in the case of the null hypothesis (using SOP makes no statistically significant difference) is the experiment ethical, but then it is also profoundly uninteresting. The rule in course-related experiments is a variant of the Hippocratic oath: before all, do not harm. The first purpose of a course is to enrich the students’ knowledge and skills; secondary aims, such as helping the professor’s research, are definitely acceptable, but must never impede the first. The setup described above is all the less acceptable that the project results presumably count towards the course grade, so the students who were forced to use the less good technique, if there demonstrably was one, have grounds to complain.

Note that Professor Smith could partially address this fairness problem by letting students choose their group, instead of assigning them randomly to group 1 or group 2 (based for example on the first letter of their names). But then the results would lose credibility, because this technique introduces self-selection and hence bias: the students who choose SOP may be the more intellectually curious students, and hence possibly the ones who do better anyway.

If Professor Smith cannot ensure fairness, he can still use students for his experiment, but has to run it outside of a course, for example by paying students, or running the experiment as a competition with some prizes for those who produce the programs with fewest bugs. This technique can work, although it introduces further dangers of self-selection. As part of a course, however, you just cannot assign students, on your own authority, to different techniques that might have an different effect on the core goal of the course: the learning experience.

So Professor Smith has a long way to go before he can run experiments that will convey a significant argument in favor of SOP.

Over the years I have seen, as a reader and sometimes as a referee, many Professor Smith papers: “empirical” evaluation of a technique by its own authors, using questionable techniques and not applying the necessary methodological precautions.

A first step is, whenever possible, to use experimenters who are from a completely different group from the developers of the ideas, as in two studies [4] [5] about the effectiveness of pair programming.

And yet! Sometimes no one else is available, and you do want to obtain objective empirical evidence about the merits of your own ideas. You are aware of the risk, and ready to face the cold reality, including if the results are unfavorable. Can you do it?

A recent attempt of ours seems to suggest that this is possible if you exert great care. It will presented in a paper at the next ESEM (Empirical Software Engineering and Measurement) and even though it discusses assessing some aspects of our own designs, using students, as part of the course project which counts for grading, and separating them into groups, we feel it was fair and ethical, and </modesty_filter_on>an ESEM referee wrote: “this is one of the best designed, conducted, and presented empirical studies I have read about recently”<modesty_filter_on>.

How did we proceed? How would you have proceeded? Think about it; feel free to express your ideas as comments to this post. In the next installment of this blog (The Professor Smith Syndrome: Part 3), I will describe our work, and let you be the judge.

References

[1] Bertrand Meyer: The rise of empirical software engineering (I): the good news, this blog, 30 July 2010, available here.
[2] Bertrand Meyer: The rise of empirical software engineering (II): what we are still missing, this blog, 31 July 2010, available here.

[3] On the Hawthorne effect, there is a good Wikipedia entry. Acknowledgment: I first heard about the Hawthorne effect from Barry Boehm.

[4] Jerzy R. Nawrocki, Michal Jasinski, Lukasz Olek and Barbara Lange: Pair Programming vs. Side-by-Side Programming, in EuroSPI 2005, pages 28-38. I do not have a URL for this article.

[5] Matthias Müller: Two controlled Experiments concerning the Comparison of Pair Programming to Peer Review, in  Journal of Systems and Software, vol. 78, no. 2, pages 166-179, November 2005; and Are Reviews an Alternative to Pair Programming ?, in  Journal of Empirical Software Engineering, vol. 9, no. 4, December 2004. I don’t have a URL for either version. I am grateful to Walter Tichy for directing me to this excellent article.

In November of 2005, as part of the festivities of its 150-th anniversary, the ETH Zurich bestowed honorary doctorates on Don Knuth and Barbara Liskov. I gave the speech (the “laudatio”). It was published in Informatik Spektrum, the journal of Gesellschaft für Informatik, the German Computer Society, vo. 29, no. 1, February 2006, pages 74-76; I came across it recently and thought others might be interested in this homage to two great computer scientists.  The beginning was in German; I translated it into English. I also replaced a couple of German expressions by their translations: “ETH commencement” for ETH-Tag (the official name of the annual ceremony) and “main building” for Hauptgebäude.

I took this picture of Wirth, Liskov and Knuth (part of my gallery of computer scientists)  later that same day.

Laudatio

 In an institution, Ladies and Gentlement, which so proudly celebrates its hundred-and-fiftieth anniversary, a relatively young disciplines sometimes has cause for envy. We computer scientists are still the babies, or at least the newest kids on the block. Outside of this building, for example, you will see streets bearing such names as Clausius, yet there is neither a Von Neumann Lane nor a a Wirth Square. Youth, however,  also has its advantages; perhaps the most striking is that we still can, in our own lifetime, meet in person some of the very founders of our discipline. No living physicist has seen Newton; no chemist has heard Lavoisier. For us, it works. Today, Ladies and Gentlemen, we have the honor of introducing two of the undisputed pioneers of informatics.

Barbara Liskov

The first of our honorees today is Professor Barbara Liskov. To understand her contributions it is essential to realize the unfair competition in which the so-called Moore’s law pits computer software against computing hardware. To match the astounding progress of computing speed and memory over the past five decades, all that we have on the software side is our own intelligence which, it is safe to say, doesn’t double every eighteen months at constant price. The key to scaling up is abstraction; all advances in programming methodology have relied on new abstraction techniques. Perhaps the most significant is data abstraction, which enables us to organize complex systems on the basis of the types of objects they manipulate, defined in completely abstract terms. This is the notion of abstract data type, a staple component today of every software curriculum, including in the very first programming course here ETH. it was introduced barely thirty years ago in a seemingly modest article in SIGPLAN Notices — the kind of publication that hardly registers a ripple in science indexes — by Barbara Liskov and Stephen Zilles. Few papers have had a more profound impact on the theory and practice of software development than this contribution, “Programming with Abstract Data Types”.

The idea of abstract data types, or ADTs, is one of those Egg of Christopher Columbus moments; a seemingly simple intuition that changes the course of things. An ADT is a class of objects described in terms not of their internal properties, but of the operations applicable to them, and the abstract properties of these operations. Not by what they are, but by what they have. A rather capitalistic view of the world, but well suited to the description of complex systems where each part knows as little as possible about the others to protect itself about their future changes.

An abstraction such as ETH-Commencement could be described in a very concrete way: it happens in a certain place, consists of one event after another, gathers so many people. This is what we computer scientists call an implementation-oriented view, and relying on it means that we can’t change any detail without endangering the consistency of other processes, such as the daily planning of room allocation in the Main Building, which use it. In an ADT view, the abstraction “ETH Commencement” is characterized not by what it is but by what it has: a start, an end, an audience, and operations such as “Schedule the ETH Commencement”, “ Reschedule it”, “Start it”, “End it”. They provide to the rest of the world a clean, precisely specified interface which enables every ADT to use every other based on the minimum properties it requires, thus isolating them from irrelevant internal changes, and providing an irreplaceable weapon in the incessant task of software engineering: battling complexity.

Barbara Liskov didn’t stay with the theoretical concepts but implemented the ideas in the CLU language, one of the most influential of the set of programming languages that in the nineteen-seventies changed our perspective of how to develop good software.

She went on to seminal work on operating systems and distributed computing, introducing several widely applied concepts such as guardians, and always backing her theoretical innovations by building practical systems, from the CLU language and compiler to the Argus and Mercury distributed operating systems. Distributed systems, such as those which banks, airlines and other global enterprises run on multiple machines across multiple networks, raise particularly challenging issues. To quote from the introduction of her article on Argus:

A centralized system is either running or crashed, but a distributed system may be partly running and partly crashed. Distributed programs must cope with failures of the underlying hardware. Both the nodes and the network may fail. The goal of Argus is to provide mechanisms that make it easier for programmers to cope with these problems.

Barbara Liskov’s work introduced seminal concepts to deal with these extremely difficult problems.

Now Ford professor of engineering at MIT, she received not long ago the prestigious John von Neumann award of the IEEE; she has been one of the most influential people in software engineering. We are grateful for how Professor Barbara Liskov has helped shape the field are honored to have her at ETH today.

 Donald Knuth

In computer science and beyond, the name of Donald Knuth carries a unique aura. A professor at Stanford since 1968, now emeritus, he is the only person on record whose job title is the title of his own book: Professor of the Art of Computer Programming. This is for his eponymous multi-volume treatise, which established the discipline of algorithm analysis, and has had more effect than any other computer science publication. The Art of Computer Programming is a marvel of breadth, depth, completeness, mathematical rigor and clarity, not to forget humor. In that legendary book you will find exposed in detail the algorithms and data structures that lie at the basis of all software applications today. A Monte Carlo simulation, as a physicists may use, requires a number sequence that is both very long and very random-looking, even though the computer is a deterministic machine; if the simulation is any good, it almost certainly relies on the devious techniques which The Art of Computer Programming presents for making a perfectly deterministic sequence appear to have no order or other recognizable property. If you are running complex programs on your laptop, and they keep creating millions of software objects without clogging up gigabytes of memory, chances are the author of the garbage collector program is using techniques he learned from Knuth, with such delightful names as “the Buddy System”. If your search engine can at the blink of an eye find a needle of useful information in a haystack of tens of billions of Web pages, it’s most likely because they’ve been indexed using finely tuned data structures, such as hash tables, for which Knuth has been the reference for three decades through volume three, Searching and Sorting.

Knuth is famous for his precision and attention to detail, going so far as to offer a financial reward for every error found in his books, although one suspects this doesn’t cost him too much since people are so proud that instead of cashing the check they have it framed for display. The other immediately striking characteristic of Knuth is how profoundly he is driven by esthetics. This applies to performing arts, as anyone who was in the Fraumünster this morning and found out who the organist was can testify, but even more to his scientific work. The very title “the Art of computer programming” betrays this. Algorithms and data structures for Knuth are never dull codes for computers, but objects of intense esthetic pleasure and friendly discussion. This concern with beauty led to a major turn in his career, which delayed the continuation of the book series by many years but resulted in a development that has affected anyone who publishes scientific text. As he received the page proofs of the second edition of one of the volumes in the late seventies he was so repelled by its physical appearance, resulting from newly introduced computer typesetting technology, that he decided to build a revolutionary font design and text processing system, all by himself, from the ground up. This resulted in a number of publications such as a long and fascinating paper in the Bulletin of the American Mathematical Society entitled “The Letter S”, but even more importantly in widely successful and practical software programs which he wrote himself, TeX and Metafont, which have today become standards for scientific publishing. Here too he has shown the way in quality and rigor, being one of the very few people in the world who promise their software to be free of bugs, and backs that promise by giving a small financial reward for any counter-example.

His numerous other contributions are far too diverse to allow even a partial mention here; they have ranged across wide areas of computer science and mathematics.

To tell the truth, we are a little embarrassed that by bringing Professor Knuth here we are delaying by a bit more the long awaited release of volume 4. But we overcome this embarrassment in time to express our pride for having Donald Erwin Knuth at ETH for this anniversary celebration.

There may be no more blatant example of  the disconnect between the software engineering community and the practice of programming than the lack of widespread recognition for the fundamental role of loop invariants. 

Let’s recall the basics, as they are taught in the fourth week or so of the ETH introductory programming course [1], from the very moment the course introduces loops. A loop is a mechanism to compute a result by successive approximations. To describe the current approximation, there is a loop invariant. The invariant must be:

1. Weak enough that we can easily ensure it on a subset, possibly trivial, of our data set. (“Easily” means than this task is substantially easier than the full problem we are trying to solve.)
2. Versatile enough that if it holds on some subset of the data we can easily (in the same sense) make it hold on a larger subset — even if only slightly larger.
3. Strong enough that, when it covers the entire data, it yields the result we seek.

As a simple example, assume we seek the maximum of an array a of numbers, indexed from 1. The invariant states that Result is the maximum of the array slice from 1 to i. Indeed:

1. We can trivially obtain the invariant by setting Result to be a [1]. (It is then the maximum of the slice a [1..1].)
2. If the invariant holds, we can extend it to a slightly larger slice — larger by just one element — by increasing i by 1 and updating Result to be the greater of the previous Result and the element a [i] (for the new  i).
3. When the slice covers the entire array — that is, i = n — the invariant tells us that Result is the maximum of the slice a [1..n], giving us the result we seek.

You cannot understand the corresponding program text

    from
        i := 1; Result := a [1]
    until i = n loop
        i := i + 1
        if Result < a [i] then Result := a [i] end
    end

without understanding the loop invariant. That is true even of people who have never heard the term: they will somehow form a mental image of the intermediate situation that justifies the algorithm. With the formal notion, the reasoning becomes precise and checkable. The difference is the same as between a builder who has no notion of theory, and one who has learned the laws of mechanics and construction engineering.

As another example, take Levenshtein distance (also known as edit distance). It is the shortest sequence of operations (insert, delete or replace a character) that will transform a string into another. The algorithm (a form of dynamic programming) fills in a matrix top to bottom and left to right, each entry being one plus the maximum of the three neighboring ones to the top and left, except if the corresponding characters in the strings are the same, in which case it keeps the top-left neighbor’s value. The basic operation in the loop body reads

      if source [i] = target [j] then
           dist [i, j] := dist [i -1, j -1]
      else
           dist [i, j] := min (dist [i, j-1], dist [i-1, j-1], dist [i-1, j]) + 1
      end

You can run this and see it work, filling the array cell after cell, then delivering the result at (dist [M, N] (the bottom-right entry, M and i being the lengths of the source and target strings. Or just watch the animation on page 60 of [2]. It works, but why it works remains a total mystery until someone tells you the invariant:

Every value of dist filled so far is the minimum distance from the initial substrings of the source, containing characters at position 1 to p, to the initial substring of the target, positions 1 to q.

This is the rationale for the above code: we want to compute the next value, at position [i, j]; if the corresponding characters in the source and target are the same, no operation is needed to extend the result we had in the top-left neighbor (position [i-1, j-1]); if not, the best we can do is the minimum we can get by extending the results obtained for our three neighbors: through the insertion of source [i] if the minimum comes from the neighbor to the left, [i-1, j]; through the deletion of target [j] if it comes from the neighbor above; or through a replacement if from the top-left neighbor.

With this explanation, a mysterious, almost hermetic algorithm instantly becomes crystal-clear. 

Yet another example is in-place linked list reversal. The body of the loop is a pointer ballet:

temp := previous
previous := next
next := next.right
previous.put_right (temp)

with proper initialization (set next to the value of first and previous to Void) and finalization (set first to the value of previous). This is not the only possible implementation, but all variants of the algorithm use a very similar scheme.

The code looks again pretty abstruse, and hard to get right if you do not remember it exactly. As in the other examples, the only way to understand it is to see the invariant, describing the intermediate assumption after a typical loop iteration. If the original situation was this:

List reversal: initial state

then after a few iterations the algorithm yields this intermediate situation: 

List reversal: intermediate state

 The figure illustrates the invariant:

Starting from previous and repeatedly following right links yields the elements of some initial part of the list, but in the reverse of their original order; starting from next and following right links yields the remaining elements, in their original order. 

Then it is clear what the loop body with its pointer ballet is about: it moves by one position to the right the boundary between the two parts, making sure that the invariant holds again in the new state, with one more element in the first (yellow) part and one fewer in the second (pink) part. At the end the second part will be empty and the first part will encompass all elements, so that (after resetting first to the value of previous) we get the desired result.

This example is particularly interesting because list reversal is a standard interview questions for programmers seeking a job; as a result, dozens of  pages around the Web helpfully present algorithms for the benefit of job candidates. I ran a search  on “List reversal algorithm” [3], which yields many such pages. It is astounding to see that from the first fifteen hits or so, which include pages from programming courses at both Stanford and MIT, not a single one mentions invariants, or (even without using the word) gives the above explanation. The situation is all the more bizarre that many of these pages — read them for yourself! — go into intricate details about variants of the pointer manipulations. There are essentially no correctness arguments.

If you go a bit further down the search results, you will find some papers that do reference invariants, but here is the catch: rather than programming or algorithms papers, they are papers about software verification, such as one by Richard Bornat which uses a low-level (C) version of the example to illustrate separation logic [4]. These are good papers but they are completely distinct from those directed at ordinary programmers, who simply wish to learn a basic algorithm, understand it in depth, and remember it on the day of the interview and beyond.

This chasm is wrong. Software verification techniques are not just good for the small phalanx of experts interested in formal proofs. The basic ideas have potential applications to the daily business of programming, as the practice of Eiffel has shown (this is the concept of  “Verification As a Matter Of Course” briefly discussed in an earlier post [5]). Absurdly, the majority of programmers do not know them.

It’s not that they cannot do their job: somehow they eke out good enough results, most of the time. After all, the European cathedrals of the middle ages were built without the benefit of sophisticated mathematical models, and they still stand. But today we would not hire a construction engineer who had not studied the appropriate mathematical techniques. Why should we make things different for software engineering, and deprive practitioners from the benefits of solid, well-accepted theory?  

As a modest first step, there is no excuse, ever, for publishing a loop without the basic evidence of its adequacy: the loop invariant.

References

[1] Bertrand Meyer: Touch of Class: Learning to Program Well, Using Objects and Contracts, Springer, 2009. See course page (English version) here.

[2] Course slides on control structures,  here in PowerPoint (or here in PDF, without the animation); see example starting on page 51, particularly the animation on page 54. More recent version in German here (and in PDF here), animation on page 60.

[3] For balance I ran the search using Qrobe, which combines results from Ask, Bing and Google.

[4] Richard Bornat, Proving Pointer Programs in Hoare Logic, in  MPC ’00, 5th International Conference on Mathematics of Program Construction, 2000, available here.

[5] Bertrand Meyer, Verification as a Matter of Course, a post on this blog.

The software world is not flat; it is multipolar. Gone are the days of one-site, one-team developments. The increasingly dominant model today is a distributed team; the place where the job gets done is the place where the appropriate people reside, even if it means that different parts of the job get done in different places.

This new setup, possibly the most important change to have affected the practice of software engineering in this early part of the millennium,  has received little attention in the literature; and even less in teaching techniques. I got interested in the topic several years ago, initially by looking at the phenomenon of outsourcing from a software engineering perspective [1]. At ETH, since 2004, Peter Kolb and I, aided by Martin Nordio and Roman Mitin, have taught a course on the topic [2], initially called “software engineering for outsourcing”. As far as I know it was the first course of its kind anywhere; not the first course about outsourcing, but the first to explore the software engineering implications, rather than business or political issues. We also teach an industry course on the same issues [3], attended since 2005 by several hundred participants, and started, with Mathai Joseph from Tata Consulting Services, the SEAFOOD conference [4], Software Engineering Advances For Outsourced and Offshore Development, whose fourth edition starts tomorrow in Saint Petersburg.

After a few sessions of the ETH course we realized that the most important property of the mode of software development explored in the course is not that it involves outsourcing but that it is distributed. In parallel I became directly involved with highly distributed development in the practice of Eiffel Software’s development. In 2007 we renamed the ETH course “Distributed and Outsourced Software Engineering” (DOSE) to acknowledge the broadened scope. The topic is still new; each year we learn a little more about what to teach and how to teach it.

The 2007 session saw another important addition. We felt it was no longer sufficient to talk about distributed development, but that students should practice it. Collaboration between groups in Zurich and other groups in Zurich was not good enough. So we contacted colleagues around the world interested in similar issues, and received an enthusiastic response. The DOSE project is itself distributed: teams from students in different universities collaborate in a single development. Typically, we have two or three geographically distributed locations in each project group. The participating universities have been Politecnico di Milano (where our colleagues Carlo Ghezzi and Elisabetta di Nitto have played a major role in the current version of the project), University of Nijny-Novgorod in Russia, University of Debrecen in Hungary, Hanoi University of Technology in Vietnam, Odessa National Polytechnic in the Ukraine and (across town for us) University of Zurich. For the first time in 2010 a university from the Western hemisphere will join: University of Rio Cuarto in Argentina.

We have extensively studied how the projects actually fare (see publications [4-8]). For students, the job is hard. Often, after a couple of weeks, many want to give up: they have trouble reaching their partner teams, understanding their accents on Skype calls, agreeing on modes of collaboration, finalizing APIs, devising a proper test plan. Yet they hang on and, in most cases, succeed. At the end of the course they tell us how much they have learned about software engineering. For example I know few better way of teaching the importance of carefully documented program interfaces — including contracts — than to ask the students to integrate their modules with code from another team halfway around the globe. This is exactly what happens in industrial software development, when you can no longer rely on informal contacts at the coffee machine or in the parking lot to smooth out misunderstandings: software engineering principles and techniques come in full swing. With DOSE, students learn and practice these fundamental techniques in the controlled environment of a university project.

An example project topic, used last year, was based on an idea by Martin Nordio. He pointed out that in most countries there are some card games played in that country only. The project was to program such a game, where the team in charge of the game logic (what would be the “business model” in an industrial project) had to explain enough of their country’s game, and abstractly enough, to enable the other team to produce the user interface, based on a common game engine started by Martin. It was tough, but some of the results were spectacular, and these are students who will not need more preaching on the importance of specifications.

We are currently preparing the next session of DOSE, in collaboration with our partner universities. The more the merrier: we’d love to have other universities participate, including from the US. Adding extra spice to the project, the topic will be chosen among those from the ICSE SCORE competition [9], so that winning students have the opportunity to attend ICSE in Hawaii. If you are teaching a suitable course, or can organize a student group that will fit, please read the project description [10] and contact me or one of the other organizers listed on the page. There is a DOSE of madness in the idea, but no one, teacher or student,  ever leaves the course bored.

References

[1] Bertrand Meyer: Offshore Development: The Unspoken Revolution in Software Engineering, in Computer (IEEE), January 2006, pages 124, 122-123. Available here.

[2] ETH course page: see here for last year’s session (description of Fall 2010 session will be added soon).

[3] Industry course page: see here for latest (June 2010( session (description of November 2010 session will be added soon).

[4] SEAFOOD 2010 home page.

[5] Bertrand Meyer and Marco Piccioni: The Allure and Risks of a Deployable Software Engineering Project: Experiences with Both Local and Distributed Development, in Proceedings of IEEE Conference on Software Engineering & Training (CSEE&T), Charleston (South Carolina), 14-17 April 2008, ed. H. Saiedian, pages 3-16. Preprint version  available online.

[6] Bertrand Meyer:  Design and Code Reviews in the Age of the Internet, in Communications of the ACM, vol. 51, no. 9, September 2008, pages 66-71. (Original version in Proceedings of SEAFOOD 2008 (Software Engineering Advances For Offshore and Outsourced Development,  Lecture Notes in Business Information Processing 16, Springer Verlag, 2009.) Available online.

[7] Martin Nordio, Roman Mitin, Bertrand Meyer, Carlo Ghezzi, Elisabetta Di Nitto and Giordano Tamburelli: The Role of Contracts in Distributed Development, in Proceedings of SEAFOOD 2009 (Software Engineering Advances For Offshore and Outsourced Development), Zurich, June-July 2009, Lecture Notes in Business Information Processing 35, Springer Verlag, 2009. Available online.

[8] Martin Nordio, Roman Mitin and Bertrand Meyer: Advanced Hands-on Training for Distributed and Outsourced Software Engineering, in ICSE 2010: Proceedings of 32th International Conference on Software Engineering, Cape Town, May 2010, IEEE Computer Society Press, 2010. Available online.

[9] ICSE SCORE 2011 competition home page.

[10] DOSE project course page.

In response to many requests, I have made available [1] the slides of my education keynote at ICSE earlier this month. The theme was “From programming to software engineering: notes of an accidental teacher”. Some of the material has been presented before, notably at the Informatics Education Europe conference in Venice in 2009. (In research you can give a new talk every month, but in education things move at a more senatorial pace.) Still, part of the content is new. The talk is a summary of my experience teaching programming and software engineering at ETH.

The usual caveats apply: these are only slides (I did not write a paper), and not all may be understandable independently of the actual talk.

Reference

[1] From programming to software engineering: notes of an accidental teacher, slides from a keynote talk at ICSE 2010.

I am blogging live from the “Cloud Futures” conference organized by Microsoft in Redmond [1]. We had two excellent keynotes today, by Ed Lazowska [1] and David Patterson.

Lazowska emphasized the emergence of a new kind of science — eScience — based on analysis of enormous amounts of data. His key point was that this approach is a radical departure from “computational science” as we know it, based mostly on large simulations. With the eScience paradigm, the challenge is to handle the zillions of bytes of data that are available, often through continuous streams, in such fields as astronomy, oceanography or biology. It is unthinkable in his view to process such data through super-computing architectures specific to an institution; the Cloud is the only solution. One of the reasons (developed more explicitly in Patterson’s talk) is that cloud computing supports scaling down as well as scaling up. If your site experiences sudden bursts of popularity — say you get slashdotted — followed by downturns, you just cannot size the hardware right.

Lazowska also noted that it is impossible to convince your average  university president that Cloud is the way to go, as he will get his advice from the science-by-simulation  types. I don’t know who the president is at U. of Washington, but I wonder if the comment would apply to Stanford?

The overall argument for cloud computing is compelling. Of course the history of IT is a succession of swings of the pendulum between centralization and delocalization: mainframes, minis, PCs, client-server, “thin clients”, “The Network Is The Computer” (Sun’s slogan in the late eighties), smart clients, Web services and so on. But this latest swing seems destined to define much of the direction of computing for a while.

Interestingly, no speaker so far has addressed issues of how to program reliably for the cloud, even though cloud computing seems only to add orders of magnitude to the classical opportunities for messing up. Eiffel and contracts have a major role to play here.

More generally the opportunity to improve quality should not be lost. There is a widespread feeling (I don’t know of any systematic studies) that a non-negligible share of results generated by computational science are just bogus, the product of old Fortran programs built by generations of graduate students with little understanding of software principles. At the very least, moving to cloud computing should encourage the use of 21-th century tools, languages and methods. Availability on the cloud should also enhance a critical property of good scientific research: reproducibility.

Software engineering is remarkably absent from the list of scientific application areas that speaker after speaker listed for cloud computing. Maybe software engineering researchers are timid, and do not think of themselves as deserving large computing resources; consider, however, all the potential applications, for example in program verification and empirical software engineering. The cloud is a big part of our own research in verification; in particular the automated testing paradigm pioneered by AutoTest [3] fits ideally with the cloud and we are actively working in this direction.

Lazowska mentioned that development environments are the ultimate application of cloud computing. Martin Nordio at ETH has developed, with the help of Le Minh Duc, a Master’s student at Hanoi University of Technology, a cloud-based version of EiffelStudio: CloudStudio, which I will present in my talk at the conference tomorrow. I’ll write more about it in later posts; just one note for the moment: no one should ever be forced again to update or commit.

References

[1] Program of the Cloud Futures conference.

[2] Keynote by Ed Lazowska. You can see his slides here.

[3] Bertrand Meyer, Arno Fiva, Ilinca Ciupa, Andreas Leitner, Yi Wei, Emmanuel Stapf: Programs That Test Themselves. IEEE Computer, vol. 42, no. 9, pages 46-55, September 2009; online version here.

Let me start, dear reader of this blog, by probing your view of equality, and also of assignment. Two questions:  

• Is a value x always equal to itself? (For the seasoned programmers in the audience: I am talking about a value, as in mathematics, not an expression, as in programming, which could have a side effect.)
• In programming, if we consider an assignment

       x := y

and v is the value of y before that assignment (again, this little detour is to avoid bothering with side effects), is the value of x always equal to v after the assignment?  

Maybe I should include here one of these Web polls that one finds on newspaper sites, so that you can vote and compare your answer to the Wisdom of Crowds. My own vote is clear: yes to both. Equality is reflexive (every value is equal to itself, at any longitude and temperature, no excuses and no exceptions); and the purpose of assignment is to make the value of the target equal to the value of the source. Such properties are some of the last ramparts of civilization. If they go away, what else is left?  

754 enters the picture

Now come floating-point numbers and the famous IEEE “754” floating-point standard [1]. Because not all floating point operations yield a result usable as a floating-point number, the standard introduces a notion of “NaN”, Not a Number; certain operations involving floating-point numbers may yield a NaN. The term NaN does not denote a single value but a set of values, distinguished by their “payloads”.  

Now assume that the value of x is a NaN. If you use a programming language that supports IEEE 754 (as they all do, I think, today) the test in  

        if x = x then …  

is supposed to yield False. Yes, that is specified in the standard: NaN is never equal to NaN (even with the same payload); nor is it equal to anything else; the result of an equality comparison involving NaN will always be False.  

Assignment behavior is consistent with this: if y (a variable, or an expression with no side effect) has a NaN value, then after  

        x := y  

the test x = y will yield False. 

Before commenting further let me note the obvious: I am by no means a numerics expert; I know that IEEE 754 was a tremendous advance, and that it was designed by some of the best minds in the field, headed by Velvel Kahan who received a Turing Award in part for that success. So it is quite possible that I am about to bury myself in piles of ridicule. On the other hand I have also learned that (1) ridicule does not kill, so I am game; and more importantly (2) experts are often right but not always, and it is always proper to question their reasoning. So without fear let me not stop at the arguments that “the committee must have voted on this point and they obviously knew what they were doing” and “it is the standard and implemented on zillions of machines, you cannot change it now”. Both are true enough, but not an excuse to censor questions.  

What are the criteria?

The question is: compatibility with an existing computer standard is great, but what about compatibility with a few hundred years of mathematics? Reflexivity of equality  is something that we expect for any data type, and it seems hard to justify that a value is not equal to itself. As to assignment, what good can it be if it does not make the target equal to the source value?  

The question of assignment is particularly vivid in Eiffel because we express the expected abstract properties of programs in the form of contracts. For example, the following “setter” procedure may have a postcondition (expressed by the ensure clause):  

        set_x (v: REAL)
                        — Set the value of x (an attribute, also of type REAL) the value of v.
                do
                        …
                        x := v  
                ensure
                        x = v
                end  

   
If you call this procedure with a NaN argument for a compiler that applies IEEE 754 semantics, and monitor contracts at run time for testing and debugging, the execution will report a contract violation. This is very difficult for a programmer to accept.  

A typical example arises when you have an assignment to an item of an array of REAL values. Assume you are executing a [i] := x. In an object-oriented view of the world (as in Eiffel), this is considered simplified syntax  for the routine call a.put (x, i). The postcondition is that a [i] = x. It will be violated!  

The experts’ view

I queried a number of experts on the topic. (This is the opportunity to express my gratitude to members of the IFIP working group 2.5 on numerical software [2], some of the world’s top experts in the field, for their willingness to respond quickly and with many insights.) A representative answer, from Stuart Feldman, was:  

If I remember the debate correctly (many moons ago), NaN represents an indefinite value, so there is no reason to believe that the result of one calculation with unclear value should match that of another calculation with unclear value. (Different orders of infinity, different asymptotic approaches toward 0/0, etc.)  

Absolutely correct! Only one little detail, though: this is an argument against using the value True as a result of the test; but it is not an argument for using the value False! The exact same argument can be used to assert that the result should not be False:  

… there is no reason to believe that the result of one calculation with unclear value should not match that of another calculation with unclear value.  

Just as convincing! Both arguments complement each other: there is no compelling reason for demanding that the values be equal; and there is no compelling argument either to demand that they be different. If you ignore one of the two sides, you are biased.  

What do we do then?

The conclusion is not that the result should be False. The rational conclusion is that True and False are both unsatisfactory solutions. The reason is very simple: in a proper theory (I will sketch it below) the result of such a comparison should be some special undefined below; the same way that IEEE 754 extends the set of floating-point numbers with NaN, a satisfactory solution would extend the set of booleans with some NaB (Not a Boolean). But there is no NaB, probably because no one (understandably) wanted to bother, and also because being able to represent a value of type BOOLEAN on a single bit is, if not itself a pillar of civilization, one of the secrets of a happy life.  

If both True and False are unsatisfactory solutions, we should use the one that is the “least” bad, according to some convincing criterion . That is not the attitude that 754 takes; it seems to consider (as illustrated by the justification cited above) that False is somehow less committing than True. But it is not! Stating that something is false is just as much of a commitment as stating that it is true. False is no closer to NaB than True is. A better criterion is: which of the two possibilities is going to be least damaging to time-honored assumptions embedded in mathematics? One of these assumptions is the reflexivity of equality:  come rain or shine, x is equal to itself. Its counterpart for programming is that after an assignment the target will be equal to the original value of the source. This applies to numbers, and it applies to a NaN as well. 

Note that this argument does not address equality between different NaNs. The standard as it is states that a specific NaN, with a specific payload, is not equal to itself.  

What do you think?

A few of us who had to examine the issue recently think that — whatever the standard says at the machine level — a programming language should support the venerable properties that equality is reflexive and that assignment yields equality.

Every programming language should decide this on its own; for Eiffel we think this should be the specification. Do you agree?  

Some theory

For readers who like theory, here is a mathematical restatement of the observations above. There is nothing fundamentally new in this section, so if you do not like strange symbols you can stop here.  

The math helps explain the earlier observation that neither True nor False is more“committing” than the other. A standard technique (coming from denotational semantics) for dealing with undefinedness in basic data types, is to extend every data type into a lattice, with a partial order relation meaning “less defined than”. The lattice includes a bottom element, traditionally written “⊥” (pronounced “Bottom”) and a top element written ⊤ (“Top”). ⊥ represents an unknown value (not enough information) and ⊤ an error value (too much information). Pictorially, the lattice for natural numbers would look like this:  

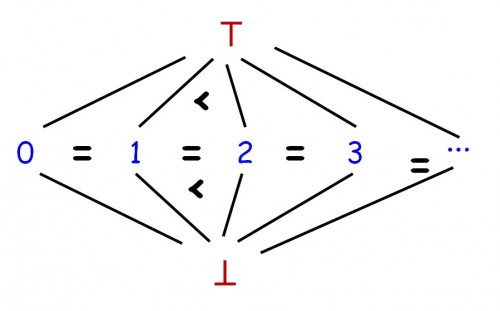
The lattice of integers

On basic types, we always use very simple lattices of this form, with three kinds of element: ⊥, less than every other element; ⊤, larger than all other elements; and in-between all the normal values of the type, which for the partial order of interest are all equal. (No, this is not a new math in which all integers are equal. The order in question simply means “is less defined than”. Every integer is as defined as all other integers, more defined than ⊥, and less defined than ⊤.) Such lattices are not very exciting, but they serve as a starting point; lattices with more interesting structures are those applying to functions on such spaces — including functions of functions —, which represent programs.  

The modeling of floating-point numbers with NaN involves such a lattice; introducing NaN means introducing a ⊥ value. (Actually, one might prefer to interpret NaN as ⊤, but the reasoning transposes immediately.)  More accurately, since there are many NaN values, the lattice will look more like this:

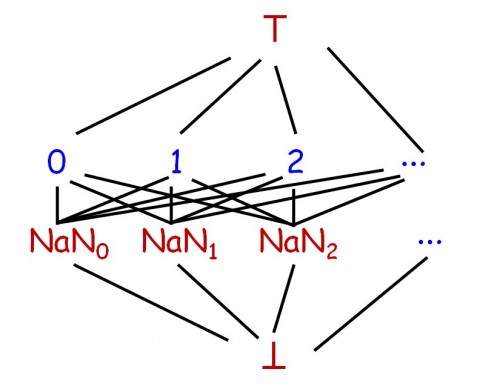
The lattice of floats in IEEE 754

For simplicity we can ignore the variety of NaNs and consider a single ⊤.

Functions on lattices — as implemented by programs — should satisfy a fundamental property: monotonicity. A function f  is monotone (as in ordinary analysis) if, whenever x ≤ y, then f (x) ≤ f (y). Monotonicity is a common-sense requirement: we cannot get more information from less information. If we know less about x than about y, we cannot expect that any function (with a computer, any program) f will, out of nowhere, restore the missing information.  

Demanding monotonicity of all floating-point operations reflects this exigency of monotonicity: indeed, in IEEE 754, any arithmetic operation — addition, multiplication … — that has a NaN as one of its arguments must yield a Nan as its result. Great. Now for soundness we should also have such a property for boolean-valued operations, such as equality. If we had a NaB as the ⊥ of booleans, just like NaN is the ⊥ of floating-point numbers,  then the result of NaN = NaN would be NaB. But the world is not perfect and the IEEE 754 standard does not govern booleans. Somehow (I think) the designers thought of False as somehow less defined than True. But it is not! False is just as defined as True in the very simple lattice of booleans; according to the partial order, True and False are equal for the relevant partial order:

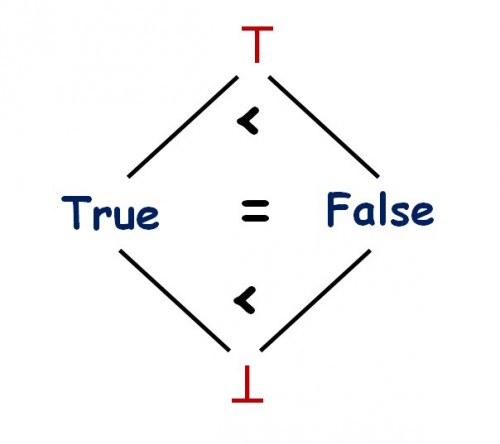
The lattice of booleans

Because any solution that cannot use a NaB will violate monotonicity and hence will be imperfect, we must resort to heuristic criteria. A very strong criterion in favor of choosing True is reflexivity — remaining compatible with a fundamental property of equality. I do not know of any argument for choosing False. 

The Spartan approach

There is, by the way, a technique that accepts booleans as we love them (with two values and no NaB) and achieves mathematical rigor. If operations involving NaNs  truly give us pimples, we can make any such operation trigger an exception. In the absence of ⊥ values,  this is an acceptable programming technique for representing undefinedness. The downside, of course, is that just about everywhere the program must be ready to handle the exception in some way. 

It is unlikely that in practice many people would be comfortable with such a solution. 

Final observations

Let me point out two objections that I have seen. Van Snyder wrote: 

NaN is not part of the set of floating-point numbers, so it doesn’t behave as if “bottom” were added to the set. 

Interesting point, but, in my opinion not applicable: ⊥ is indeed not part of the mathematical set of floating point numbers, but in the form of NaN it is part of the corresponding type (float in C, REAL in Eiffel); and the operations of the type are applicable to all values, including NaN if, as noted, we have not taken the extreme step of triggering an exception every time an operation uses a NaN as one of its operands. So we cannot free ourselves from the monotonicity concern by just a sleight of hands. 

Another comment, also by Van Snyder (slightly abridged): 

Think of [the status of NaN] as a variety of dynamic run-time typing. With static typing, if  x is an integer variable and y

        x := y 

does not inevitably lead to 

        x = y

 True; and a compelling argument to require that conversions satisfy equality as a postcondition! Such  reasoning — reflexivity again — was essential in the design of the Eiffel conversion mechanism [3], which makes it possible to define conversions between various data types (not just integers and reals and the other classical examples, but also any other user types as long as the conversion does not conflict with inheritance). The same conversion rules apply to assignment and equality, so that yes, whenever the assignment x := y is permitted, including when it involves a conversion, the property x = y  is afterwards always guaranteed to hold.

It is rather dangerous indeed to depart from the fundamental laws of mathematics. 

References

[1] IEEE floating-point standard, 754-2008; see summary and references in the Wikipedia entry.  

[2] IFIP Working Group 2.5 on numerical software: home page. 

[3] Eiffel standard (ECMA and ISO), available on the ECMA site.

New variants of the loop construct have been introduced into Eiffel, allowing a safer, more concise and more abstract style of programming. The challenge was to remain compatible with the basic loop concept, in particular correctness concerns (loop invariant and loop variant), to provide a flexible mechanism that would cover many different cases of iteration, and to keep things simple.

Here are some examples of the new forms. Consider a structure s, such as a list, which can be traversed in sequence. The following loop prints all elements of the list:

      across s as c loop print (c.item) end

(The procedure print is available on all types, and can be adapted to any of them by redefining the out feature; item gives access to individual values of the list.) More about c in just a moment; in the meantime you can just consider consider that using “as c” and manipulating the structure through c rather than directly through s  is a simple idiom to be learned and applied systematically for such across loops.

The above example is an instruction. The all and some variants yield boolean expressions, as in

across s as c all c.item > 0 end

which denotes a boolean value, true if and only if all elements of the list are positive. To find out if at least one is positive, use

across s as c some c.item > 0 end

Such expressions could appear, for example, in a class invariant, but they may be useful in many different contexts.

In some cases, a from clause is useful, as in

        across s as c from sum := 0  loop sum := sum + c.index ∗ c.item end
— Computes Σ i * s [i]

The original form of loop in Eiffel is more explicit, and remains available; you can achieve the equivalent of the last example, on a suitable structure, as

A list and a cursor

      from
sum := 0 ; s.start
until
s.after
loop
sum := sum + s.index ∗ s.item
s.forth
        end

which directly manipulates a cursor through s, using start to move it to the beginning, forth to advance it, and after to test if it is past the last element. The forms with across achieve the same purpose in a more concise manner. More important than concision is abstraction: you do not need to worry about manipulating the cursor through start, forth and after. Under the hood, however, the effect is the same. More precisely, it is the same as in a loop of the form

from
sum := 0 ; c.start
until
c.after
loop
sum := sum + c.index ∗ c.item
c.forth
        end

where c is a cursor object associated with the loop. The advantage of using a cursor is clear: rather than keeping the state of the iteration in the object itself, you make it external, part of a cursor object that, so to speak, looks at the list. This means in particular that many traversals can be active on the same structure at the same time; with an internal cursor, they would mess up with each other, unless you manually took the trouble to save and restore cursor positions. With an external cursor, each traversal has its own cursor object, and so does not interfere with other traversals — at least as long as they don’t change the structure (I’ll come back to that point).

With the across variant, you automatically use a cursor; you do not have to declare or create it: it simply comes as a result of the “as c” part of the construct, which introduces c as the cursor.

On what structures can you perform such iterations? There is no limitation; you simply need a type based on a class that inherits, directly or indirectly, from the library class ITERABLE. All relevant classes from the EiffelBase library have been updated to provide this inheritance, so that you can apply the across scheme to lists of all kinds, hash tables, arrays, intervals etc.

One of these structures is the integer interval. The notation  m |..| n, for integers m and n, denotes the corresponding integer interval. (This is not a special language notation, simply an operator, |..|, defined with the general operator mechanism as an alias for the feature interval of INTEGER classes.) To iterate on such an interval, use the same form as in the examples above:

        across m |..| n  as c from sum := 0  loop sum := sum + a [c.item] end
— Computes Σ a [i], for i ranging from m to n, for an array (or other structure) a. 

The key feature in ITERABLE is new_cursor, which returns a freshly created cursor object associated with the current structure. By default it is an ITERATION_CURSOR, the most general cursor type, but every descendant of ITERABLE can redefine the result type to something more specific to the current structure. Using a cursor — c in the above examples —, rather than manipulating the structure s directly, provides considerable flexibility thanks to the property that ITERATION_CURSOR itself inherits from ITERABLE   and hence has all the iteration mechanisms. For example you may write

across s.new_cursor.reversed as c loop print (c.item) end

to print elements in reverse order. (Using Eiffel’s operator  mechanism, you may write – s.new_cursor, with a minus operator, as a synonym for new_cursor.reversed.) The function reversed gives you a new cursor on the same target structure, enabling you to iterate backwards. Or you can use

        across s.new_cursor + 3 as c loop print (c.item) end

(using s.new_cursor.incremented (3) rather than s.new_cursor + 3 if you are not too keen on operator syntax) to iterate over every third item. A number of other possibilities are available in the cursor classes.

A high-level iteration mechanism is only safe if you have the guarantee that the structure remains intact throughout the iteration. Assume you are iterating through a structure

across s   as c loop some_routine end

and some_routine changes the structure s: the whole process could be messed up. Thanks to Design by Contract mechanisms, the library protects you against such mistakes. Features such as item and index, accessing properties of the structure during the iteration, are equipped with a precondition clause

require
is_valid

and every operation that changes the structure sets is_valid to false. So as soon as any change happens, you cannot continue the iteration; all you can do is restart a new one; the command start, used internally to start the operation, does not have the above precondition.

Sometimes, of course, you do want to change a structure while traversing it; for example you may want to add an element just to the right of the iteration position. If you know what you are doing that’s fine. (Let me correct this: if you know what you are doing, express it through precise contracts, and you’ll be fine.) But then you should not use the abstract forms of the loop, across…; you should control the iteration itself through the basic form from … until … with explicit cursor manipulation, protected by appropriate contracts.

The two styles, by the way, are not distinct constructs. Eiffel has always had only one form of loop and this continues the case. The across forms are simply new possibilities added to the classical loop construct, with obvious constraints stating for example that you may not have both a some or all form and an explicit  loop body.  In particular, an across loop can still have an invariant clause , specifying the correctness properties of the loop, as in

        across s as c from sum := 0  invariant sum = sigma (s, index)  loop sum := sum + c.index ∗ c.item end

EiffelStudio 6.5 already included the language update; the library update (not yet including the is_valid preconditions for data structure classes) will be made available this week.

These new mechanisms should increase the level of abstraction and the reliability of loops, a fundamental element of  almost all programs.

My textbook Touch of Class: An Introduction to Programming Well Using Objects and Contracts [1] is now available from Springer Verlag [2]. I have been told of many bookstores in Europe that have it by now; for example Amazon Germany [3] offers immediate delivery. Amazon US still lists the book as not yet published [4], but I think this will be corrected very soon.

The book results from six years of teaching introductory programming at ETH Zurich. It is richly illustrated in full color (not only with technical illustrations but with numerous photographs of people and artefacts). It is pretty big, but designed so that a typical one-semester introductory course can cover most of the material.

Many topics are addressed (see table of contents below), including quite a few that are seldom seen at the introductory level. Some examples, listed here in random order: a fairly extensive introduction to software engineering including things like requirements engineering (not usually mentioned in programming courses, with results for everyone to see!) and CMMI, a detailed discussion of how to implement recursion, polymorphism and dynamic binding and their role for software architecture, multiple inheritance, lambda calculus (at an introductory level of course), a detailed analysis of the Observer and Visitor patterns, event-driven programming, the lure and dangers of references and aliasing, topological sort as an example of both algorithm and API design, high-level function closures, software tools, properties of computer hardware relevant for programmers, undecidability etc.

The progression uses an object-oriented approach throughout; the examples are in Eiffel, and four appendices present the details of Java, C#, C++ and C. Concepts of Design by Contract and rigorous development are central to the approach; for example, loops are presented as a technique for computing a result by successive approximation, with a central role for the concept of loop invariant. This is not a “formal methods” book in the sense of inflicting on the students a heavy mathematical apparatus, but it uses preconditions, postconditions and invariants throughout to alert them to the importance of reasoning rigorously about programs. The discussion introduces many principles of sound design, in line with the book’s subtitle, “Learning to Program Well”.

The general approach is “Outside-In” (also known as “Inverted Curriculum” and described at some length in some of my articles, see e.g. [5]): students have, right from the start, the possibility of working with real software, a large (150,000-line) library that has been designed specifically for that purpose. Called Traffic, this library simulates traffic in a city; it is graphical and of good enough visual quality to be attractive to today’s “Wii generation” students, something that traditional beginners’ exercises, like computing the 7-th Fibonacci number, cannot do (although we have these too as well). Using the Traffic software through its API, students can right from the first couple of weeks produce powerful applications, without understanding the internals of the library. But they do not stop there: since the whole thing is available in open source, students learn little by little how the software is made internally. Hence the name “Outside-In”: understand the interface first, then dig into the internals. Two advantages of the approach are particularly worth noting:

• It emphasizes the value of abstraction, and particular contracts, not by preaching but by showing to students that abstraction helps them master a large body of professional-level software, doing things that would otherwise be unthinkable at an introductory level.
• It addresses what is probably today the biggest obstacle to teaching introductory programming: the wide diversity of initial student backgrounds. The risk with traditional approaches is either to fly too high and lose the novices, or stay too low and bore those who already have programming experience. With the Outside-In method the novices can follow the exact path charted from them, from external API to internal implementation; those who already know something about programming can move ahead of the lectures and start digging into the code by themselves for information and inspiration.

(We have pretty amazing data on students’ prior programming knowledge, as  we have been surveying students for the past six years, initially at ETH and more recently at the University of York in England thanks to our colleague Manuel Oriol; some day I will post a blog entry about this specific topic.)

The book has been field-tested in its successive drafts since 2003 at ETH, for the Introduction to Programming course (which starts again in a few weeks, for the first time with the benefit of the full text in printed form). Our material, such as a full set of slides, plus exercises, video recordings of the lectures etc. is available to any instructor selecting the text. I must say that Springer did an outstanding job with the quality of the printing and I hope that instructors, students, and even some practitioners already in industry will like both form and content.

Table of contents

Front matter: Community resource, Dedication (to Tony Hoare and Niklaus Wirth), Prefaces, Student_preface, Instructor_preface, Note to instructors: what to cover?, Contents

PART I: Basics
1 The industry of pure ideas
2 Dealing with objects
3 Program structure basics
4 The interface of a class
5 Just Enough Logic
6 Creating objects and executing systems
7 Control structures
8 Routines, functional abstraction and information hiding
9 Variables, assignment and references
PART II: How things work
10 Just enough hardware
11 Describing syntax
12 Programming languages and tools
PART III: Algorithms and data structures
13 Fundamental data structures, genericity, and algorithm complexity
14 Recursion and trees
15 Devising and engineering an algorithm: Topological Sort
PART IV: Object-Oriented Techniques
16 Inheritance
17 Operations as objects: agents and lambda calculus
18 Event-driven design
PART V: Towards software engineering
19 Introduction to software engineering
PART VI: Appendices
A An introduction to Java (from material by Marco Piccioni)
B An introduction to C# (from material by Benjamin Morandi)
C An introduction to C++ (from material by Nadia Polikarpova)
D From C++ to C
E Using the EiffelStudio environment
Picture credits
Index

References

[1] Bertrand Meyer, Touch of Class: An Introduction to Programming Well Using Objects and Contracts, Springer Verlag, 2009, 876+lxiv pages, Hardcover, ISBN: 978-3-540-92144-8.

[2] Publisher page for [1]: see  here. List price: $79.95. (The page says “Ships in 3 to 4 weeks” but I think this is incorrect as the book is available; I’ll try to get the mention corrected.)

[3] Amazon.de page: see here. List price: EUR 53.45 (with offers starting at EUR 41.67).

[4] Amazon.com page: see here. List price: $63.96.

[5] Michela Pedroni and Bertrand Meyer: The Inverted Curriculum in Practice, in Proceedings of SIGCSE 2006, ACM, Houston (Texas), 1-5 March 2006, pages 481-485; available online.