Bertrand Meyer's technology+ blog

In a previous post I briefly mentioned some work that I am doing on aliasing. There is a draft paper [1], describing the theory, calculus, graphical notation (alias diagrams) and implementation. Here I will try to give an idea of what it’s about, with the hope that you will be intrigued enough to read the article. Even before you read it you might try out the implementation[2], a simple interactive interface with all the examples of the article .

What the article does not describe in detail — that will be for a companion paper— is how the calculus will be used as part of a general framework for developing object-oriented software proved correct from the start, the focus of our overall  “Trusted Components” project’ [3]. Let me simply state that the computation of aliases is the key missing step in the effort to make correctness proofs a standard part of software development. This is a strong claim which requires some elaboration, but not here.

The alias calculus asks a simple question: given two expressions representing references (pointers),  can their values, at a given point in the program, ever reference the same object during execution?

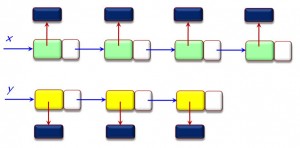
As an example  application, consider two linked lists x and y, which can be manipulated with operations such as extend, which creates a new cell and adds it at the end of the list:

 The calculus makes it possible to prove that if  x and y are not aliased to each other, then none of the pointers in any of the cells in either of the lists can point to  (be aliased to) any cell of  the other. If  x is initially aliased to y, the property no longer holds. You can run the proof (examples 18 and 19) in the downloadable implementation.

The calculus gives a set of rules, each applying to a particular construct of the language, and listed below.

The rule for a construct p is of the form

          a |= p      =   a’ 

where a and a’ are alias relations; this states that executing p  in a state where the alias relation is a will yield the alias relation a’ in the resulting state. An alias relation is a symmetric, irreflexive relation; it indicates which expressions and variables can be aliased to each other in a given state.

The constructs p considered in the discussion are those of a simplified programming language; a modern object-oriented language such as Eiffel can easily be translated into that language. Some precision will be lost in the process, meaning that the alias calculus (itself precise) can find aliases that would not exist in the original program; if this prevents proofs of desired properties, the cut instruction discussed below serves to correct the problem.

The first rule is for the forget instruction (Eiffel: x := Void):

          a |= forget x       =   a \- {x}

where the \- operator removes from a relation all the elements belonging to a given set A. In the case of object-oriented programming, with multidot expressions x.y.z, the application of this rule must remove all elements whose first component, here x, belongs to A.

The rule for creation is the same as for forget:

         a |= create x          =   a \- {x}

The two instructions have different semantics, but the same effect on aliasing.

The calculus has a rule for the cut instruction, which removes the connection between two expressions:

        a |= cut x, y       =   a — <x, y>

where — is set difference and <x, y> includes the pairs [x, y] and [y, x] (this is a special case of a general notation defined in the article, using the overline symbol). The cut   instruction corresponds, in Eiffel, to cut   x /= y end:  a hint given to the alias calculus (and proved through some other means, such as standard axiomatic semantics) that some references will not be aliased.

The rule for assignment is

      a |= (x := y)      =   given  b = a \- {x}   then   <b È {x} x (b / y)}> end

where b /y (“quotient”), similar to an equivalence class in an equivalence relation, is the set of elements aliased to y in b, plus y itself (remember that the relation is irreflexive). This rule works well for object-oriented programming thanks to the definition of the \- operator: in x := x.y, we must not alias x to x.y, although we must alias it to any z that was aliased to x.y.

The paper introduces a graphical notation, alias diagrams, which makes it possible to reason effectively about such situations. Here for example is a diagram illustrating the last comment:

Alias diagram for a multidot assignment

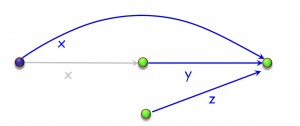
(The grayed elements are for explanation and not part of the final alias relation.)

For the compound instruction, the rule is:

           a |= (p ;  q)      =   (a |= p) |= q)

For the conditional instruction, we get:

           a |= (then p else  q end)      =   (a |= p) È  (a |= q)

Note the form of the instruction: the alias calculus ignores information from the then clause present in the source language. The union operator is the reason why  alias relations,  irreflexive and symmetric, are not  necessarily transitive.

The loop instruction, which also ignores the test (exit or continuation condition), is governed by the following rule:

           a |= (loop p end)       =   t_N

where span style=”color: #0000ff;”>N is the first value such that t_N = t_N+1 (in other words, t_N is the fixpoint) in the following sequence:

            t₀          =    a
           t_n+1       =   (t_n È (t_n |= p))     

The existence of a fixpoint and the correctness of this formula to compute it are the result of a theorem in the paper, the “loop aliasing theorem”; the proof is surprisingly elaborate (maybe I missed a simpler one).

For procedures, the rule is

         a |= call p        =   a |= p.body

where p.body is the body of the procedure. In the presence of recursion, this gives rise to a set of equations, whose solution is the fixpoint; again a theorem is needed to demonstrate that the fixpoint exists. The implementation directly applies fixpoint computation (see examples 11 to 13 in the paper and implementation).

The calculus does not directly consider routine arguments but treats them as attributes of the corresponding class; so a call is considered to start with assignments of the form f : = a for every pair of formal and actual arguments f and a. Like the omission of conditions in loops and conditionals, this is a source of possible imprecision in translating from an actual programming language into the calculus, since values passed to recursive activations of the same routine will be conflated.

Particularly interesting is the last rule, which generalizes the previous one to qualified calls of the form x. f (…)  as they exist in object-oriented programming. The rule involves the new notion of inverse variable, written x’ where x is a variable. Laws of the calculus (with Current denoting the current object, one of the fundamental notions of object-oriented programming) are

        Current.x            = x   
        x.Current            = x
        x.x’                      = Current
        x’.x                      = Current

In other words, Current plays the role of zero element for the dot operator, and variable inversion is the inverse operation. In a call x.f, where x denotes the supplier object (the target of the call), the inverse variable provides a back reference to the client object (the caller), indispensable to interpret references in the original context. This property is reflected by the qualified client rule, which uses  the auxiliary operator n (where x n a, for a relation a and a variable x, is the set of pairs [x.u, y.v] such that the pair [u, v] is in a). The rule is:

         a |= call x.r       =   x n ((x’ n a ) |= call r)

You need to read the article for the full explanation, but let me offer the following quote from the corresponding section (maybe you will note a familiar turn of phrase):

Thus we are permitted to prove that the unqualified call creates certain aliasings, on the assumption that it starts in its own alias environment but has access to the caller’s environment through the inverted variable, and then to assert categorically that the qualified call has the same aliasings transposed back to the original environment. This change of environment to prove the unqualified property, followed by a change back to the original environment to prove the qualified property, explains well the aura of magic which attends a programmer’s first introduction to object-oriented programming.

I hope you will enjoy the calculus and try the examples in the implementation. It is fun to apply, and there seems to be no end to the potential applications.

Reference

[1] Bertrand Meyer: The Theory and Calculus of Aliasing, draft paper, first published 12 January 2009 (revised 21 January 2010), available here and also at arxiv.org.
[2] Implementation (interactive version to try all the examples of the paper): downloadable Windows executable here.
[3] Bertrand Meyer: The Grand Challenge of Trusted Components, in 2003 International Conference on Software Engineering, available here.