Eiffel

Getting a program right, in nine episodes

by

About this article: it originated as a series of posts on the Communications of the ACM blog. I normally repost such articles here. (Even though copy-paste is usually not good, there are three reasons for this duplication: the readership seems to be largely disjoint; I can use better formatting, since their blog software is more restrictive than WordPress; and it is good to have a single repository for all my articles, including both those who originated on CACM and those who did not.) The series took the form of nine articles, where each of the first few ended with a quiz, to which the next one, published a couple of days later, provided an answer. Since all these answers are now available it would make no sense to use the same scheme, so I am instead publishing the whole thing as a single article  with nine sections, slightly adapted from the original.

I was too lazy so far to collect all the references into a single list, so numbers such as [1] refer to the list at the end of the corresponding section.

A colleague recently asked me to present a short overview of  axiomatic semantics as a guest lecture in one of his courses. I have been teaching courses on software verification for a long time (see e.g. here), so I have plenty of material; but instead of just reusing it, I decided to spend a bit of time on explaining why it is good to have a systematic approach to software verification. Here is the resulting tutorial.

 

1. Introduction and attempt #1

Say “software verification” to software professionals, or computer science students outside of a few elite departments, and most of them will think  “testing”. In a job interview, for example, show a loop-based algorithm to a programmer and ask “how would you verify it?”: most will start talking about devising clever test cases.

Far from me to berate testing [1]; in fact, I have always thought that the inevitable Dijkstra quote about testing — that it can only show the presence of errors, not their absence [2] — which everyone seems to take as an indictment and dismissal of testing (and which its author probably intended that way) is actually a fantastic advertisement for testing: a way to find bugs? Yes! Great! Where do I get it?  But that is not the same as verifying the software, which means attempting to ascertain that it has no bugs.

Until listeners realize that verification cannot just mean testing, the best course material on axiomatic semantics or other proof techniques will not attract any interest. In fact, there is somewhere a video of a talk by the great testing and public-speaking guru James Whittaker where he starts by telling his audience not to worry, this won’t be a standard boring lecture, he will not start talking about loop invariants [3]! (Loop invariants are coming in this article, in fact they are one of its central concepts, but in later sections only, so don’t bring the sleeping bags yet.) I decided to start my lecture by giving an example of what happens when you do not use proper verification. More than one example, in fact, as you will see.

A warning about this article: there is nothing new here. I am using an example from my 1990 book Introduction to the Theory of Programming Languages (exercise 9.12). Going even further back, a 1983 “Programming Pearls” Communications of the ACM article by Jon Bentley [4] addresses the same example with the same basic ideas. Yet almost forty years later these ideas are still not widely known among practitioners. So consider these articles as yet another tutorial on fundamental software engineering stuff.

The tutorial is a quiz. We start with a program text:

from

i := 1 ; j := n              — Result initialized to 0.

until i = j loop

m := (i + j) // 2         — Integer division

if t [m] ≤ x then i := m  else  j := m end

end

if x = t [i] then Result := i end

All variables are of integer type. t is an up-sorted array of integers, indexed from 1 to n . We do not let any notation get between friends. A loop from p until e loop q end executes p then, repeatedly: stops if e (the exit condition) is true, otherwise executes q. (Like {p ; while not e do {q}} in some other notations.) “:=” is assignment, “=” equality testing.  “//” is integer division, e.g. 6 //3 = 7 //3 = 2. Result is the name of a special variable whose final value will be returned by this computation (as part of a function, but we only look at the body). Result is automatically initialized to zero like all integer variables, so if execution does not assign anything to Result the function will return zero.

First question: what is this program trying to do?

OK, this is not the real quiz. I assume you know the answer: it is an attempt at “binary search”, which finds an element in the array, or determines its absence, in a sequence of about log2 (n) steps, rather than n if we were use sequential search.  (Remember we assume the array is sorted.) Result should give us a position where x appears in the array, if it does, and otherwise be zero.

Now for the real quiz: does this program meet this goal?

The answer should be either yes or no. (If no, I am not asking for a correct version, at least not yet, and in any case you can find some in the literature.) The situation is very non-symmetric, we might say Popperian:

  • To justify a no answer it suffices of a single example, a particular array t and a particular value x, for which the program fails to set Result as it should.
  • To justify a yes answer we need to provide a credible argument that for every t and  x the program sets Result as it should.

Notes to section 1

[1] The TAP conference series (Tests And Proofs), which Yuri Gurevich and I started, explores the complementarity between the two approaches.

[2] Dijkstra first published his observation in 1969. He did not need consider the case of infinite input sets: even for a trivial finite program that multiplies two 32-bit integers, the number of cases to be examined, 264, is beyond human reach. More so today with 64-bit integers. Looking at this from a 2020 perspective, we may note that exhaustive testing of a finite set of cases, which Dijkstra dismissed as impossible in practice, is in fact exactly what the respected model checking verification technique does; not on the original program, but on a simplified — abstracted — version precisely designed to keep the number of cases tractable. Dijkstra’s argument remains valid, of course, for  the original program if non-trivial. And model-checking does not get us out of the woods: while we are safe if its “testing” finds no bug, if it does find one we have to ensure that the bug is a property of the original program rather than an artifact of the abstraction process.

[3] It is somewhere on YouTube, although I cannot find it right now.

[4] Jon Bentley: Programming Pearls: Writing Correct Programs, in Communications of the ACM, vol. 26, no. 12, pp. 1040-1045, December 1983, available for example here.

2. Attempt #2

Was program #1 correct? If so it should yield the correct answer. (An answer is correct if either Result is the index in t of an element equal to x, or Result = 0 and x does not appear in t.)

This program is not correct. To prove that it is not correct it suffices of a single example (test case) for which the program does not  “yield the correct answer”. Assume x = 1 and the array t has two elements both equal to zero (n = 2, remember that arrays are indexed from 1):

t = [0   0]

The successive values of the variables and expressions are:

                                            m       i          j            i + j + 1

After initialization:                   1         2                3

i ≠ j, so enter loop:           1       1        2                 6         — First branch of “if” since t [1] ≤ x
— so i gets assigned the value of m

But then neither of the values of i and j has changed, so the loop will repeat its body identically (taking the first branch) forever. It is not even that the program yields an incorrect answer: it does not yield an answer at all!

Note (in reference to the famous Dijkstra quote mentioned in the first article), that while it is common to pit tests against proofs, a test can actually be a proof: a test that fails is a proof that the program is incorrect. As valid as the most complex mathematical proof. It may not be the kind of proof we like most (our customers tend to prefer a guarantee that the program is correct), but it is a proof all right.

We are now ready for the second attempt:

—  Program attempt #2.

from

i := 1 ; j := n

until i = j or Result > 0  loop

m := (i + j) // 2         — Integer division

if t [m] ≤ x then

i := m  + 1

elseif t [m] = x then

Result := m

else                         — In this case t [m] > x

j := m – 1

end

end

Unlike the previous one this version always changes i or j, so we may hope it does not loop forever. It has a nice symmetry between i and j.

Same question as before: does this program meet its goal?

3. Attempt #3

The question about program #2, as about program #1: was: it right?

Again no.  A trivial example disproves it: n = 1, the array t contains a single element t [1] = 0, x = 0. Then the initialization sets both i and j to 1, i = j holds on entry to the loop which stops immediately, but Result is zero whereas it should be 1 (the place where x appears).

Here now is attempt #3, let us see it if fares better:

—  Program attempt #3.

from

i := 1 ; j := n

until i = j loop

m := (i + j + 1) // 2

if t [m] ≤ x then

i := m  + 1

else

j := m

end

end

if 1  ≤ i  and i ≤ n then Result := i end
       — If not, Result remains 0.

What about this one?

3. Attempt #4 (also includes 3′)

The first two program attempts were wrong. What about the third?

I know, you have every right to be upset at me, but the answer is no once more.

Consider a two-element array t = [0 0] (so n = 2, remember that our arrays are indexed from 1 by convention) and a search value x = 1. The successive values of the variables and expressions are:

                                                  m          i          j            i + j + 1

After initialization:                            1        2           4

i ≠ j, so enter loop:               2           3        2          6                  — First branch of “if” since t [2] < x

i ≠ j,  enter loop again:        3           ⚠                                       — Out-of-bounds memory access!
— (trying to access non-existent t [3])

Oops!

Note that we could hope to get rid of the array overflow by initializing i to 0 rather than 1. This variant (version #3′) is left as a bonus question to the patient reader. (Hint: it is also not correct. Find a counter-example.)

OK, this has to end at some point. What about the following version (#4): is it right?

—  Program attempt #4.

from

i := 0 ; j := n + 1

until i = j loop

m := (i + j) // 2

if t [m] ≤ x then

i := m  + 1

else

j := m

end

end

if 1 ≤ i  and i ≤ n then Result := i end

5. Attempt #5

Yes, I know, this is dragging on. But that’s part of the idea: witnessing how hard it is to get a program right if you just judging by the seat of your pants. Maybe we can get it right this time?

Are we there yet? Is program attempt #4 finally correct?

Sorry to disappoint, but no. Consider a two-element array t = [0 0], so n = 2, and a search value x = 1 (yes, same counter-example as last time, although here we could also use x = 0). The successive values of the variables and expressions are:

                                                 m          i          j            i + j

After initialization:                           0        3           3

i ≠ j, so enter loop:               1           2       3          5            — First branch of “if”

i ≠ j, enter loop again:         2         3        3         6            — First branch again

i = j, exit loop

The condition of the final “if” is true, so Result gets the value 3. This is quite wrong, since there is no element at position 3, and in any case x does not appear in t.

But we are so close! Something like this should work, should it not?

So patience, patience, let us tweak it just one trifle more, OK?

—  Program attempt #5.

from

i := 1 ; j := n + 1

until i ≥ j or Result > 0 loop

m := (i + j) // 2

if t [m] < x then

i := m + 1

elseif  t [m] > x then

j := m

else

Result := m

end

end

Does it work now?

6. Attempt #6

The question about program #5  was the same as before: is it right, is it wrong?

Well, I know you are growing more upset at me with each section, but the answer is still that this program is wrong. But the way it is wrong is somewhat specific; and it applies, in fact, to all previous variants as well.

This particular wrongness (fancy word for “bug”) has a history. As I pointed out in the first article, there is a long tradition of using binary search to illustrate software correctness issues. A number of versions were published and proved correct, including one in the justly admired Programming Pearls series by Jon Bentley. Then in 2006 Joshua Bloch, then at Google, published a now legendary blog article [2] which showed that all these versions suffered from a major flaw: to obtain m, the approximate mid-point between i and j, they compute

(i + j) // 2

which, working on computer integers rather than mathematical integers, might overflow! This in a situation in which both i and j, and hence m as well, are well within the range of the computer’s representable integers, 2-n to 2n (give or take 1) where n is typically 31 or, these days, 63, so that there is no conceptual justification for the overflow.

In the specification that I have used for this article, i starts at 1, so the problem will only arise for an array that occupies half of the memory or more, which is a rather extreme case (but still should be handled properly). In the general case, it is often useful to use arrays with arbitrary bounds (as in Eiffel), so we can have even a small array, with high indices, for which the computation will produce an overflow and bad results.

The Bloch gotcha is a stark reminder that in considering the correctness of programs we must include all relevant aspects and consider programs as they are executed on a real computer, not as we wish they were executed in an ideal model world.

(Note that Jon Bentley alluded to this requirement in his original article: while he did not explicitly mention integer overflow, he felt it necessary to complement his proof by the comment that that  “As laborious as our proof of binary search was, it is still unfinished by some standards. How would you prove that the program is free of runtime errors (such as division by zero, word overflow, or array indices out of bounds)?” Prescient words!)

It is easy to correct the potential arithmetic overflow bug: instead of (i + j) // 2, Bloch suggested we compute the average as

i + (j – i) // 2

which is the same from a mathematician’s viewpoint, and indeed will compute the same value if both variants compute one, but will not overflow if both i and j are within range.

So we are ready for version 6, which is the same as version 5 save for that single change:

—  Program attempt #6.

from

i := 1 ; j := n + 1

until i ≥ j or Result > 0 loop

m := i + (j – i) // 2

if t [m] < x then

i := m + 1

elseif  t [m] > x then

j := m

else

Result := m

end

end

Now is probably the right time to recall the words by which Donald Knuth introduces binary search in the original 1973 tome on Sorting and Searching of his seminal book series The Art of Computer Programming:knuth

Although the basic idea of binary search is comparatively straightforward, the details can be somewhat tricky, and many good programmers have done it wrong the first few times they tried.

Do you need more convincing? Be careful what you answer, I have more variants up my sleeve and can come up with many more almost-right-but-actually-wrong program attempts if you nudge me. But OK, even the best things have an end. This is not the last section yet, but that was the last program attempt. To the naturally following next question in this running quiz,  “is version 6 right or wrong”, I can provide the answer: it is, to the best of my knowledge, a correct program. Yes! [3].

But the quiz continues. Since answers to the previous questions were all  that the programs were not correct, it sufficed in each case to find one case for which the program did not behave as expected. Our next question is of a different nature: can you find an argument why version #6 is correct?

References for section 6

[1] (In particular) Jon Bentley: Programming Pearls — Writing Correct Programs, in Communications of the ACM, vol. 26, no. 12, December 1983, pages 1040-1045, available here.

[2] Joshua Bloch: Extra, Extra — Read All About It: Nearly All Binary Searches and Mergesorts are Broken, blog post, on the Google AI Blog, 2 June 2006, available here.

[3] A caveat: the program is correct barring any typos or copy-paste errors — I am starting from rigorously verified programs (see the next posts), but the blogging system’s UI and text processing facilities are not the best possible for entering precise technical text such as code. However carefully I check, I cannot rule out a clerical mistake, which of course would be corrected as soon as it is identified.

7. Using a program prover

Preceding sections presented candidate binary search algorithms and asked whether they are correct. “Correct” means something quite precise: that for an array t and a value x, the final value of the variable Result is a valid index of t (that is to say, is between 1 and n, the size of t) if and only if x appears at that index in t.

The last section boldly stated that program attempt #6 was correct. The question was: why?

In the case of the preceding versions, which were incorrect, you could prove that property, and I do mean prove, simply by exhibiting a single counter-example: a single t and x for which the program does not correctly set Result. Now that I asserting the program to be correct, one example, or a million examples, do not suffice. In fact they are almost irrelevant. Test as much as you like and get correct results every time, you cannot get rid of the gnawing fear that if you had just tested one more time after the millionth test you would have produced a failure. Since the set of possible tests is infinite there is no solution in sight [1].

We need a proof.

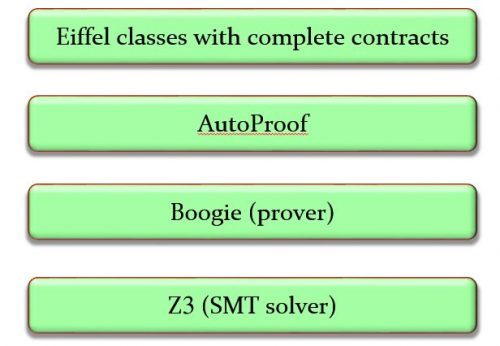
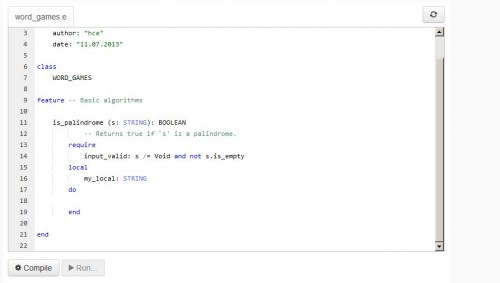
I am going to explain that proof in the next section, but before that I would like to give you an opportunity to look at the proof by yourself. I wrote in one of the earlier articles that most of what I have to say was already present in Jon Bentley’s 1983 Programming Pearls contribution [2], but a dramatic change did occur in the four decades since: the appearance of automated proof system that can handle significant, realistic programs. One such system, AutoProof, was developed at the Chair of Software engineering at ETH Zurich [3] (key project members were Carlo Furia, Martin Nordio, Nadia Polikarpova and Julian Tschannen, with initial contributions by Bernd Schoeller) on the basis of the Boogie proof technology from Microsoft Research).

AutoProof is available for online use, and it turns out that one of the basic tutorial examples is binary search. You can go to the corresponding page and run the proof.

I am going to let you try this out (and, if you are curious, other online AutoProof examples as well) without too many explanations; those will come in the next section. Let me simply name the basic proof technique: loop invariant. A loop invariant is a property INV associated with a loop, such that:

  • A. After the loop’s initialization, INV will hold.
  • B. One execution of the loop’s body, if started with INV satisfied (and the loop’s exit condition not satisfied, otherwise we wouldn’t be executing the body!), satisfies INV again when it terminates.

This idea is of course the same as that of a proof by induction in mathematics: the initialization corresponds to the base step (proving that P (0) holds) and the body property to the induction step (proving that from P (n) follows P (n + 1). With a traditional induction proof we deduce that the property (P (n)) holds for all integers. For the loop, we deduce that when the loop finishes its execution:

  • The invariant still holds, since executing the loop means executing the initialization once then the loop body zero or more times.
  • And of course the exit condition also holds, since otherwise we would still be looping.

That is how we prove the correctness of a loop: the conjunction of the invariant and the exit condition must yield the property that we seek (in the example, the property, stated above of Result relative to t and x).

We also need to prove that the loop does terminate. This part involves another concept, the loop’s variant, which I will explain in the next section.

For the moment I will not say anything more and let you look at the AutoProof example page (again, you will find it here), run the verification, and read the invariant and other formal elements in the code.

To “run the verification” just click the Verify button on the page. Let me emphasize (and emphasize again and again and again) that clicking Verify will not run the code. There is no execution engine in AutoProof, and the verification does not use any test cases. It processes the text of the program as it appears on the page and below. It applies mathematical techniques to perform the proof; the core property to be proved is that the proposed loop invariant is indeed invariant (i.e. satisfies properties A and B above).

The program being proved on the AutoProof example page is version #6 from the last section, with different variable names. So far for brevity I have used short names such as i, j and m but the program on the AutoProof site applies good naming practices with variables called low, up, middle and the like. So here is that version again with the new variable names:

—  Program attempt #7  (identical to #6 with different variable names) .

from

low := 0 ; up := n

until low ≥ up or Result > 0 loop

middle := low + ((up – low) // 2)

if a [middle] < value then      — The array is now called a rather than t

low := middle + 1

elseif  a [middle] > value then

up := middle

else

Result := middle

end

end

This is exactly the algorithm text on the AutoProof page, the one that you are invited to let AutoProof verify for you. I wrote “algorithm text” rather than “program text” because the actual program text (in Eiffel) includes variant and invariant clauses which do not affect the program’s execution but make the proof possible.

Whether or not these concepts (invariant, variant, program proof) are completely new to you, do try the prover and take a look at the proof-supporting clauses. In the next article I will remove any remaining mystery.

Note and references for section 7

[1] Technically the set of possible [array, value] pairs is finite, but of a size defying human abilities. As I pointed out in the first section, the “model checking” and “abstract interpretation” verification techniques actually attempt to perform an exhaustive test anyway, after drastically reducing the size of the search space. That will be for some other article.

[2]  Jon Bentley: Programming Pearls: Writing Correct Programs, in Communications of the ACM, vol. 26, no. 12, pp. 1040-1045, December 1983, available for example here.

[3] The AutoProof page contains documentations and numerous article references.

8. Understanding the proof

The previous section invited you to run the verification on the AutoProof tutorial page dedicated to the example. AutoProof is an automated proof system for programs. This is just a matter of clicking  “Verify”, but more importantly, you should read the annotations added to the program text, particularly the loop invariant, which make the verification possible. (To avoid any confusion let me emphasize once more that clicking “Verify” does not run the program, and that no test cases are used; the effect is to run the verifier, which attempts to prove the correctness of the program by working solely on the program text.)

Here is the program text again, reverting for brevity to the shorter identifiers (the version on the AutoProof page has more expressive ones):

from

i := 1 ; j := n + 1

until i ≥ j or Result > 0 loop

m := i + (j – i) // 2

if t [m] < x then

i := m + 1

elseif  t [m] > x then

j := m

else

Result := m

end

end

Let us now see what makes the proof possible. The key property is the loop invariant, which reads

A:   1  ≤ i  ≤ j  ≤ n + 1
B:   0  ≤ Result  ≤ n
C:   ∀ k: 1 .. i –1  |  t [k] < x
D:   ∀ k: j .. n  |  t [k] > x
E:    (Result > 0)   ⇒   (t [Result] = x)

The notation is slightly different on the Web page to adapt to the Eiffel language as it existed at the time it was produced; in today’s Eiffel you can write the invariant almost as shown above. Long live Unicode, allowing us to use symbols such as ∀ (obtained not by typing them but by using smart completion, e.g. you start typing “forall” and you can select the ∀ symbol that pops up), ⇒ for  “implies” and many others

Remember that the invariant has to be established by the loop’s initialization and preserved by every iteration. The role of each of its clauses is as follows:

  • A: keep the indices in range.
  • B: keep the variable Result, whose final value will be returned by the function, in range.
  • C and D: eliminate index intervals in which we have determined that the sought value, x, does not appear. Before i, array values are smaller; starting at j, they are greater. So these two intervals, 1..i and j..n, cannot contain the sought value. The overall idea of the algorithm (and most other search algorithms) is to extend one of these two intervals, so as to narrow down the remaining part of 1..n where x may appear.
  • E: express that as soon as we find a positive (non-zero) Result, its value is an index in the array (see B) where x does appear.

Why is this invariant useful? The answer is that on exit it gives us what we want from the algorithm. The exit condition, recalled above, is

i ≥ j or Result > 0

Combined with the invariant, it tells us that on exit one of the following will hold:

  • Result > 0, but then because of E we know that x appears at position Result.
  • i < j, but then A,  C and D  imply that x does not appear anywhere in t. In that case it cannot be true that Result > 0, but then because of B Result must be zero.

What AutoProof proves, mechanically, is that under the function’s precondition (that the array is sorted):

  • The initialization ensures the invariant.
  • The loop body, assuming that the invariant is satisfied but the exit condition is not, ensures the loop invariant again after it executes.
  • The combination of the invariant and the exit condition ensures, as just explained, the postcondition of the function (the property that Result will either be positive and the index of an element equal to x, or zero with the guarantee that x appears nowhere in t).

Such a proof guarantees the correctness of the program if it terminates. We (and AutoProof) must prove separately that it does terminate. The technique is simple: find a “loop variant”, an integer quantity v  which remains non-negative throughout the loop (in other words, the loop invariant includes or implies v ≥ 0) and decreases on each iteration, so that the loop cannot continue executing forever. An obvious variant here is j – i + 1 (where the + 1 is needed because j – i may go down to -1 on the last iteration if x does not appear in the array). It reflects the informal idea of the algorithm: repeatedly decrease an interval i .. j – 1 (initially, 1 .. n) guaranteed to be such that x appears in t if and only if it appears at an index in that interval. At the end, either we already found x or the interval is empty, implying that x does not appear at all.

A great reference on variants and the techniques for proving program termination is a Communications of the ACM article of 2011: [3].

The variant gives an upper bound on the number of iterations that remain at any time. In sequential search, j – i + 1 would be our best bet; but for binary search it is easy to show that  log2  (j – i + 1) is also a variant, extending the proof of correctness with a proof of performance (the key goal of binary search being to ensure a logarithmic rather than linear execution time).

This example is, I hope, enough to highlight the crucial role of loop invariants and loop variants in reasoning about loops. How did we get the invariant? It looks like I pulled it out of a hat. But in fact if we go the other way round (as advocated in classic books [1] [2]) and develop the invariant and the loop together the process unfolds itself naturally and there is nothing mysterious about the invariant.

Here I cannot resist quoting (thirty years on!) from my own book Introduction to the Theory of Programming Languages [4]. It has a chapter on axiomatic semantics (also known as Hoare logic, the basis for the ideas used in this discussion), which I just made available: see here [5]. Its exercise 9.12 is the starting point for this series of articles. Here is how the book explains how to design the program and the invariant [6]:

In the general case [of search, binary or not] we aim for a loop body of the form

m := ‘‘Some value in 1.. n such that i ≤ m < j’’;

if t [m] ≤ x then

i := m + 1

else

j := m

end

It is essential to get all the details right (and easy to get some wrong):

  • The instruction must always decrease the variant j – i, by increasing i or decreasing j. If the the definition of m specified just m ≤ j rather than m < j, the second branch would not meet this goal.
  •  This does not transpose directly to i: requiring i < m < j would lead to an impossibility when j – i is equal to 1. So we accept i ≤ m but then we must take m + 1, not m, as the new value of i in the first branch.
  •  The conditional’s guards are tests on t [m], so m must always be in the interval 1 . . n. This follows from the clause 0 ≤ i ≤ j ≤ n + 1 which is part of the invariant.
  •  If this clause is satisfied, then m ≤ n and m > 0, so the conditional instruction indeed leaves this clause invariant.
  • You are invited to check that both branches of the conditional also preserve the rest of the invariant.
  • Any policy for choosing m is acceptable if it conforms to the above scheme. Two simple choices are i  and j – 1; they lead to variants of the sequential search algorithm [which the book discussed just before binary search].

For binary search, m will be roughly equal to the average of i and j.

“Roughly” because we need an integer, hence the // (integer division).

In the last section, I will reflect further on the lessons we can draw from this example, and the practical significance of the key concept of invariant.

References and notes for section 8

[1] E.W. Dijkstra: A Discipline of Programming, Prentice Hall, 1976.

[2] David Gries: The Science of Programming, Springer, 1989.

[3] Byron Cook, Andreas  Podelski and Andrey Rybalchenko: Proving program termination, in Communications of the ACM, vol. 54, no. 11, May 2011, pages 88-98, available here.

[4] Bertrand Meyer, Introduction to the Theory of Programming Languages, Prentice Hall, 1990. The book is out of print but can be found used, e.g. on Amazon. See the next entry for an electronic version of two chapters.

[5] Bertrand Meyer Axiomatic semantics, chapter 9 from [3], available here. Note that the PDF was reconstructed from an old text-processing system (troff); the figures could not be recreated and are missing. (One of these days I might have the patience of scanning them from a book copy and adding them. Unless someone wants to help.) I also put online, with the same caveat, chapter 2 on notations and mathematical basis: see here.

[6] Page 383 of [4] and [5]. The text is verbatim except a slight adaptation of the programming notation and a replacement of the variables: i in the book corresponds to i – 1 here, and j to j – 1. As a matter of fact I prefer the original conventions from the book (purely as a matter of taste, since the two are rigorously equivalent), but I changed here to the conventions of the program as it appears in the AutoProof page, with the obvious advantage that you can verify it mechanically. The text extract is otherwise exactly as in the 1990 book.

9. Lessons learned

What was this journey about?

We started with a succession of attempts that might have “felt right” but were in fact all wrong, each in its own way: giving the wrong answer in some cases, crashing (by trying to access an array outside of its index interval) in some cases, looping forever in some cases. Always “in some cases”,  evidencing the limits of testing, which can never guarantee that it exercises all the problem cases. A correct program is one that works in all cases. The final version was correct; you were able to prove its correctness with an online tool and then to understand (I hope) what lies behind that proof.

To show how to prove such correctness properties, I have referred throughout the series to publications from the 1990s (my own Introduction to The Theory of Programming Languages), the 1980s (Jon Bentley’s Programming Pearls columns, Gries’s Science of Programming), and even the 1970s (Dijkstra’s Discipline of Programming). I noted that the essence of my argument appeared in a different form in one of Bentley’s Communications articles. What is the same and what has changed?

The core concepts have been known for a long time and remain applicable: assertion, invariant, variant and a few others, although they are much better understood today thanks to decades of theoretical work to solidify the foundation. Termination also has a more satisfactory theory.

On the practical side, however, the progress has been momentous. Considerable engineering has gone into making sure that the techniques scaled up. At the time of Bentley’s article, binary search was typical of the kind of programs that could be proved correct, and the proof had to proceed manually. Today, we can tackle much bigger programs, and use tools to perform the verification.

Choosing binary search again as an example today has the obvious advantage that everyone can understand all the details, but should not be construed as representative of the state of the art. Today’s proof systems are far more sophisticated. Entire operating systems, for example, have been mechanically (that is to say, through a software tool) proved correct. In the AutoProof case, a major achievement was the proof of correctness [1] of an entire data structure (collections) library, EiffelBase 2. In that case, the challenge was not so much size (about 8,000 source lines of code), but the complexity of both:

  • The scope of the verification, involving the full range of mechanisms of a modern object-oriented programming language, with classes,  inheritance (single and multiple), polymorphism, dynamic binding, generics, exception handling etc.
  • The code itself, using sophisticated data structures and algorithms, involving in particular advanced pointer manipulations.

In both cases, progress has required advances on both the science and engineering sides. For example, the early work on program verification assumed a bare-bones programming language, with assignments, conditionals, loops, routines, and not much more. But real programs use many other constructs, growing ever richer as programming languages develop. To cover exception handling in AutoProof required both theoretical modeling of this construct (which appeared in [2]) and implementation work.

More generally, scaling up verification capabilities from the small examples of 30 years ago to the sophisticated software that can be verified today required the considerable effort of an entire community. AutoProof, for example, sits at the top of a tool stack relying on the Boogie environment from Microsoft Research, itself relying on the Z3 theorem prover. Many person-decades of work make the result possible.

tool_stack

Beyond the tools, the concepts are esssential. One of them, loop invariants, has been illustrated in the final version of our program. I noted in the first article the example of a well-known expert and speaker on testing who found no better way to announce that a video would not be boring than  “relax, we are not going to talk about loop invariants.” Funny perhaps, but unfair. Loop invariants are one of the most beautiful concepts of computer science. Not so surprisingly, because loop invariants are the application to programming of the concept of mathematical induction. According to the great mathematician Henri Poincaré, all of mathematics rests on induction; maybe he exaggerated, maybe not, but who would think of teaching mathematics without explaining induction? Teaching programming without explaining loop invariants is no better.

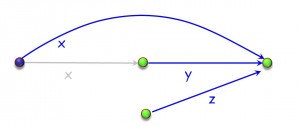
Below is an illustration (if you will accept my psychedelic diagram) of what a loop is about, as a problem-solving technique. Sometimes we can get the solution directly. Sometimes we identify several steps to the solution; then we use a sequence (A ; B; C). Sometimes we can find two (or more) different ways of solving the problem in different cases; then we use a conditional (if c then A else B end). And sometimes we can only get a solution by getting closer repeatedly, not necessarily knowing in advance how many times we will have to advance towards it; then, we use a loop.

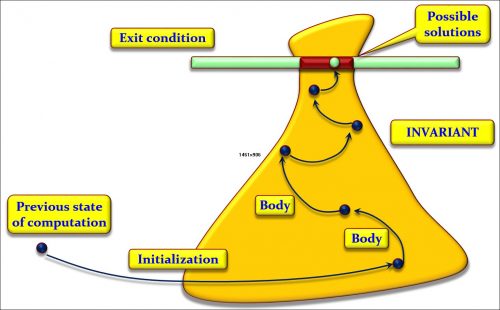
loop_strategy

We identify an often large (i.e. very general) area where we know the solution will lie; we call that area the loop invariant. The solution or solutions (there may be more than one) will have to satisfy a certain condition; we call it the exit condition. From wherever we are, we shoot into the invariant region, using an appropriate operation; we call it the initialization. Then we execute as many times as needed (maybe zero if our first shot was lucky) an operation that gets us closer to that goal; we call it the loop body. To guarantee termination, we must have some kind of upper bound of the distance to the goal, decreasing each time discretely; we call it the loop variant.

This explanation is only an illustration, but I hope it makes the ideas intuitive. The key to a loop is its invariant. As the figure suggests, the invariant is always a generalization of the goal. For example, in binary search (and many other search algorithms, such as sequential search), our goal is to find a position where either x appears or, if it does not, we can be sure that it appears nowhere. The invariant says that we have an interval with the same properties (either x appears at a position belonging to that interval or, if it does not, it appears nowhere). It obviously includes the goal as a special case: if the interval has length 1, it defines a single position.

An invariant should be:

  1. Strong enough that we can devise an exit condition which in the end, combined with the invariant, gives us the goal we seek (a solution).
  2. Weak enough that we can devise an initialization that ensures it (by shooting into the yellow area) easily.
  3. Tuned so that we can devise a loop body that, from a state satifying the invariant, gets us to a new one that is closer to the goal.

In the example:

  1. The exit condition is simply that the interval’s length is 1. (Technically, that we have computed Result as the single interval element.) Then from the invariant and the exit condition, we get the goal we want.
  2. Initialization is easy, since we can just take the initial interval to be the whole index range of the array, which trivially satisfies the invariant.
  3. The loop body simply decreases the length of the interval (which can serve as loop variant to ensure termination). How we decrease the length depends on the search strategy; in sequential search, each iteration decreases the length by 1, correct although not fast, and binary search decreases it by about half.

The general scheme always applies. Every loop algorithm is characterized by an invariant. The invariant may be called the DNA of the algorithm.

To demonstrate the relevance of this principle, my colleagues Furia, Velder, and I published a survey paper [6] in ACM Computing Surveys describing the invariants of important algorithms in many areas of computer science, from search algorithms to sorting (all major algorithms), arithmetic (long integer addition, squaring), optimization and dynamic programming  (Knapsack, Levenshtein/Edit distance), computational geometry (rotating calipers), Web (Page Rank)… I find it pleasurable and rewarding to go deeper into the basis of loop algorithms and understand their invariants; like a geologist who does not stop at admiring the mountain, but gets to understand how it came to be.

Such techniques are inevitable if we want to get our programs right, the topic of this article. Even putting aside the Bloch average-computation overflow issue, I started with 5 program attempts, all kind of friendly-looking but wrong in different ways. I could have continued fiddling with the details, following my gut feeling to fix the flaws and running more and more tests. Such an approach can be reasonable in some cases (if you have an algorithm covering a well-known and small set of cases), but will not work for non-trivial algorithms.

Newcomers to the concept of loop invariant sometimes panic: “this is all fine, you gave me the invariants in your examples, how do I find my own invariants for my own loops?” I do not have a magic  recipe (nor does anyone else), but there is no reason to be scared. Once you have understood the concept and examined enough examples (just a few of those in [6] should be enough), writing the invariant at the same time as you are devising a loop will come as a second nature to you.

As the fumbling attempts in the first few sections should show, there is not much of an alternative. Try this approach. If you are reaching these final lines after reading what preceded them, allow me to thank you for your patience, and to hope that this rather long chain of reflections on verification will have brought you some new insights into the fascinating challenge of writing correct programs.

References

[1] Nadia Polikarpova, Julian Tschannen, and Carlo A. Furia: A Fully Verified Container Library, in Proceedings of 20th International Symposium on Formal Methods (FM 15), 2015. (Best paper award.)

[2] Martin Nordio, Cristiano Calcagno, Peter Müller and Bertrand Meyer: A Sound and Complete Program Logic for Eiffel, in Proceedings of TOOLS 2009 (Technology of Object-Oriented Languages and Systems), Zurich, June-July 2009, eds. M. Oriol and B. Meyer, Springer LNBIP 33, June 2009.

[3] Boogie page at MSR, see here for publications and other information.

[4] Z3 was also originally from MSR and has been open-sourced, one can get access to publications and other information from  its Wikipedia page.

[5] Carlo Furia, Bertrand Meyer and Sergey Velder: Loop invariants: Analysis, Classification and Examples, in ACM Computing Surveys, vol. 46, no. 3, February 2014. Available here.

[6] Dynamic programming is a form of recursion removal, turning a recursive algorithm into an iterative one by using techniques known as “memoization” and  “bottom-up computation” (Berry). In this transformation, the invariant plays a key role. I will try to write this up some day as it is a truly elegant and illuminating explanation.

Learning to program, online

by

Introduction to Programming MOOCThe ETH introductory programming course, which I have taught since 2003 and used as the basis for the Springer Touch of Class textbook, is now available as a MOOC: an online course, open to anyone interested [1]. The project was started and led by Marco Piccioni.

The MOOC was released in September; although it was “open” (the other “O”) from the start, we have not publicized it widely until now, since we used it first for the benefit of students taking the course at ETH, and took advantage of this experience to polish it. If you follow the acronym buzz you may say it was first a “SPOC” (Small Personal Online Course”). The experience with our students has been extremely encouraging: they took it as a supplement to the lectures and widely praised its value.We hope that many others will find it useful as well.

MOOCs are hot but they have attracted as much criticism as hype. We have seen the objections: low completion rates, lack of direct human contact, threats to traditional higher education. Two things are clear, though: MOOCs are more than a passing fad; and they have their own pedagogical advantages.

MOOCs are here to stay; one ignores them at one’s own peril. For courses on a popular topic, I believe that in a few years almost everyone will be teaching from a MOOC. Not in the sense of telling students “just follow this course on the Web and come back for the exam“, but as a basis for individual institutions’ courses. For example the students might be told to take the lessons online, then come to in-person lectures (“Flip The Classroom“) or discussion sessions. For any given topic, such as introduction to programming, only a handful of MOOCs will emerge in this role. We would like the ETH course to be one of them.

The question is not just to replace courses and textbooks with an electronic version. MOOCs enrich the learning experience. Introduction to Programming is a particularly fertile application area for taking advantage of technology: the presentation of programming methods and techniques becomes even more effective if students can immediately try out the ideas, compile the result, run it, and see the results on predefined tests. Our course offers many such interactive exercises, thanks to the E4Mooc (Eiffel for MOOCs) framework developed by Christian Estler [2]. This feature has proved to be a key attraction of the course for ETH students. Here for example is an exercise asking you to write a function that determines whether a string is a palindrome (reads identically in both directions):

The program area is pre-filled with a class skeleton where all that remains for you to enter is the algorithm for the relevant function. Then you can click “Compile” and, if there are no compilation errors, “Run” to test your candidate code against a set of predefined test values. One of the benefits for users taking the course is that there is no software to install: everything runs in the cloud, accessible from the browser. Here we see the MOOC not just as a technique for presenting standard material but as an innovative learning tool, opening up pedagogical techniques that were not previously possible.

Besides E4Mooc, our course relies on the Moodle learning platform. Our experience with Moodle has been pleasant; we noticed, for example, that students really liked the Moodle feature enabling them to gain virtual “badges” for good answers, to the point of repeating exercises until they got the badges. For instructors preparing the course, building a MOOC is a huge amount of work (that was not a surprise, people had told us); but it is worth the effort.

We noted that attendance at the lectures increased as compared to previous years. The matter is a natural concern: other than the cold November mornings in Zurich (one of the lectures is at 8 AM) there are many reasons not to show up in class:  the textbook covers much of the material; all the slides are online; so are the slides for exercise sessions (tutorials) and texts of exercises and some earlier exams; lectures were video-recorded in previous years, and students can access the old recordings. Our feeling is that the MOOC makes the course more exciting and gives students want to come to class and hear more.

The MOOC course is not tied to a particular period; you can take it whenever you like. (The current practice of offering MOOCs at fixed times is disappointing: what is the point of putting a course online if participants are forced to fit to a fixed schedule?)

Marco Piccioni and I are now off to our second MOOC, which will be a generalization of the first, covering the basics not just of programming but of computer science and IT overall, and will be available on one of the major MOOC platforms. We will continue to develop the existing MOOC, which directly supports our in-person course, and which we hope will be of use to many other people.

Take the MOOC, or tell a beginner near you to take it, and tell us what you think.

References

[1] Bertrand Meyer, Marco Piccioni and other members of the ETH Chair of Software Engineering: ETH Introduction to Programming MOOC, available here.

[2] H-Christian Estler, E4Mooc demo, available on YouTube: here.

Reading notes: strong specifications are well worth the effort

by

 

This report continues the series of ICSE 2013 article previews (see the posts of these last few days, other than the DOSE announcement), but is different from its predecessors since it talks about a paper from our group at ETH, so you should not expect any dangerously delusional,  disingenuously dubious or downright deceptive declaration or display of dispassionate, disinterested, disengaged describer’s detachment.

The paper [1] (mentioned on this blog some time ago) is entitled How good are software specifications? and will be presented on Wednesday by Nadia Polikarpova. The basic result: stronger specifications, which capture a more complete part of program functionality, cause only a modest increase in specification effort, but the benefits are huge; in particular, automatic testing finds twice as many faults (“bugs” as recently reviewed papers call them).

Strong specifications are specifications that go beyond simple contracts. A straightforward example is a specification of a push operation for stacks; in EiffelBase, the basic Eiffel data structure library, the contract’s postcondition will read

item = x                                          /A/
count = old count + 1

where x is the element being pushed, item the top of the stack and count the number of elements. It is of course sound, since it states that the element just pushed is now the new top of the stack, and that there is one more element; but it is also  incomplete since it says nothing about the other elements remaining as they were; an implementation could satisfy the contract and mess up with these elements. Using “complete” or “strong” preconditions, we associate with the underlying domain a theory [2], or “model”, represented by a specification-only feature in the class, model, denoting a sequence of elements; then it suffices (with the convention that the top is the first element of the model sequence, and that “+” denotes concatenation of sequences) to use the postcondition

model = <x> + old model         /B/

which says all there is to say and implies the original postconditions /A/.

Clearly, the strong contracts, in the  /B/ style, are more expressive [3, 4], but they also require more specification effort. Are they worth the trouble?

The paper explores this question empirically, and the answer, at least according to the criteria used in the study, is yes.  The work takes advantage of AutoTest [5], an automatic testing framework which relies on the contracts already present in the software to serve as test oracles, and generates test cases automatically. AutoTest was applied to both to the classic EiffelBase, with classic partial contracts in the /A/ style, and to the more recent EiffelBase+ library, with strong contracts in the /B/ style. AutoTest is for Eiffel programs; to check for any language-specificity in the results the work also included testing a smaller set of classes from a C# library, DSA, for which a student developed a version (DSA+) equipped with strong model-based contracts. In that case the testing tool was Microsoft Research’s Pex [7]. The results are similar for both languages: citing from the paper, “the fault rates are comparable in the C# experiments, respectively 6 . 10-3 and 3 . 10-3 . The fault complexity is also qualitatively similar.”

The verdict on the effect of strong specifications as captured by automated testing is clear: the same automatic testing tools applied to the versions with strong contracts yield twice as many real faults. The term “real fault” comes from excluding spurious cases, such as specification faults (wrong specification, right implementation), which are a phenomenon worth studying but should not count as a benefit of the strong specification approach. The paper contains a detailed analysis of the various kinds of faults and the corresponding empirically determined measures. This particular analysis is for the Eiffel code, since in the C#/Pex case “it was not possible to get an evaluation of the faults by the original developers“.

In our experience the strong specifications are not that much harder to write. The paper contains a precise measure: about five person-weeks to create EiffelBase+, yielding an “overall benefit/effort ratio of about four defects detected per person-day“. Such a benefit more than justifies the effort. More study of that effort is needed, however, because the “person” in the person-weeks was not just an ordinary programmer. True, Eiffel experience has shown that most programmers quickly get the notion of contract and start applying it; as the saying goes in the community, “if you can write an if-then-else, you can write a contract”. But we do not yet have significant evidence of whether that observation extends to model-based contracts.

Model-based contracts (I prefer to call them “theory-based” because “model” means so many other things, but I do not think I will win that particular battle) are, in my opinion, a required component of the march towards program verification. They are the right compromise between simple contracts, which have proved to be attractive to many practicing programmers but suffer from incompleteness, and full formal specification à la Z, which say everything but require too much machinery. They are not an all-or-nothing specification technique but a progressive one: programmers can start with simple contracts, then extend and refine them as desired to yield exactly the right amount of precision and completeness appropriate in any particular context. The article shows that the benefits are well worth the incremental effort.

According to the ICSE program the talk will be presented in the formal specification session, Wednesday, May 22, 13:30-15:30, Grand Ballroom C.

References

[1] Nadia Polikarpova, Carlo A. Furia, Yu Pei, Yi Wei and Bertrand Meyer: What Good Are Strong Specifications?, to appear in ICSE 2013 (Proceedings of 35th International Conference on Software Engineering), San Francisco, May 2013, draft available here.

[2] Bertrand Meyer: Domain Theory: the forgotten step in program verification, article on this blog, see here.

[3] Bernd Schoeller, Tobias Widmer and Bertrand Meyer: Making Specifications Complete Through Models, in Architecting Systems with Trustworthy Components, eds. Ralf Reussner, Judith Stafford and Clemens Szyperski, Lecture Notes in Computer Science, Springer-Verlag, 2006, available here.

[4] Nadia Polikarpova, Carlo Furia and Bertrand Meyer: Specifying Reusable Components, in Verified Software: Theories, Tools, Experiments (VSTTE ‘ 10), Edinburgh, UK, 16-19 August 2010, Lecture Notes in Computer Science, Springer Verlag, 2010, available here.

[5] Bertrand Meyer, Ilinca Ciupa, Andreas Leitner, Arno Fiva, Yi Wei and Emmanuel Stapf: Programs that Test Themselves, IEEE Computer, vol. 42, no. 9, pages 46-55, September 2009, also available here.

[6] Bertrand Meyer, Ilinca Ciupa, Andreas Leitner, Arno Fiva, Yi Wei and Emmanuel Stapf: Programs that Test Themselves, in IEEE Computer, vol. 42, no. 9, pages 46-55, September 2009, also available here.

[7] Nikolai Tillman and Peli de Halleux, Pex: White-Box Generation for .NET, in Tests And Proofs (TAP 2008), pp. 134-153.

 

New course partners sought: a DOSE of software engineering education

by

 

Since 2007 we have conducted, as part of a course at ETH, the DOSE project, Distributed and Outsourced Software Engineering, developed by cooperating student teams from a dozen universities around the world. We are finalizing the plans for the next edition, October to December 2013, and will be happy to welcome a few more universities.

The project consists of building a significant software system collaboratively, using techniques of distributed software development. Each university contributes a number of “teams”, typically of two or three students each; then “groups”, each made up of three teams from different universities, produce a version of the project.

The project’s theme has varied from year to year, often involving games. We make sure that the development naturally divides into three subsystems or “clusters”, so that each group can quickly distribute the work among its teams. An example of division into clusters, for a game project, is: game logic; database and player management; user interface. The page that describes the setup in more detail [1] has links enabling you to see the results of some of the best systems developed by students in recent years.

The project is a challenge. Students are in different time zones, have various backgrounds (although there are minimum common requirements [1]), different mother tongues (English is the working language of the project). Distributed development is always hard, and is harder in the time-constrained context of a university course. (In industry, while we do not like that a project’s schedule slips, we can often survive if it does; in a university, when the semester ends, we have to give students a grade and they go away!) It is typical, after the initial elation of meeting new student colleagues from exotic places has subsided and the reality of interaction sets in, that some groups will after a month, just before the first or second deadline, start to panic — then take matters into their own hands and produce an impressive result. Students invariably tell us that they learn a lot through the course; it is a great opportunity to practice the principles of modern software engineering and to get prepared for the realities of today’s developments in industry, which are in general distributed.

For instructors interested in software engineering research, the project is also a great way to study issues of distributed development in  a controlled setting; the already long list of publications arising from studies performed in earlier iterations [3-9] suggests the wealth of available possibilities.

Although the 2013 project already has about as many participating universities as in previous years, we are always happy to consider new partners. In particular it would be great to include some from North America. Please read the requirements on participating universities given in [1]; managing such a complex process is a challenge in itself (as one can easily guess) and all teaching teams must share goals and commitment.

References

[1] General description of DOSE, available here.

[2] Bertrand Meyer: Offshore Development: The Unspoken Revolution in Software Engineering, in Computer (IEEE), January 2006, pages 124, 122-123, available here.

[3] Bertrand Meyer and Marco Piccioni: The Allure and Risks of a Deployable Software Engineering Project: Experiences with Both Local and Distributed Development, in Proceedings of IEEE Conference on Software Engineering & Training (CSEE&T), Charleston (South Carolina), 14-17 April 2008, available here.

[4] Martin Nordio, Roman Mitin, Bertrand Meyer, Carlo Ghezzi, Elisabetta Di Nitto and Giordano Tamburelli: The Role of Contracts in Distributed Development, in Proceedings of Software Engineering Advances For Offshore and Outsourced Development, Lecture Notes in Business Information Processing 35, Springer-Verlag, 2009, available here.

[5] Martin Nordio, Roman Mitin and Bertrand Meyer: Advanced Hands-on Training for Distributed and Outsourced Software Engineering, in Proceedings of the 32nd ACM/IEEE International Conference on Software Engineering – Volume 1, ACM. 2010 available here.

[6] Martin Nordio, Carlo Ghezzi, Bertrand Meyer, Elisabetta Di Nitto, Giordano Tamburrelli, Julian Tschannen, Nazareno Aguirre and Vidya Kulkarni: Teaching Software Engineering using Globally Distributed Projects: the DOSE course, in Collaborative Teaching of Globally Distributed Software Development – Community Building Workshop (CTGDSD — an ICSE workshop), ACM, 2011, available here.

[7] Martin Nordio, H.-Christian Estler, Bertrand Meyer, Julian Tschannen, Carlo Ghezzi, and Elisabetta Di Nitto: How do Distribution and Time Zones affect Software Development? A Case Study on Communication, in Proceedings of the 6th International Conference on Global Software Engineering (ICGSE), IEEE, pages 176–184, 2011, available here.

[8] H.-Christian Estler, Martin Nordio, Carlo A. Furia, and Bertrand Meyer: Distributed Collaborative Debugging, to appear in Proceedings of 7th International Conference on Global Software Engineering (ICGSE), 2013.

[9] H.-Christian Estler, Martin Nordio, Carlo A. Furia, and Bertrand Meyer: Unifying Configuration Management with Awareness Systems and Merge Conflict Detection, to appear in Proceedings of the 22nd Australasian Software Engineering Conference (ASWEC), 2013.

 

All Bugs Great and Small

by

(Acknowledgment: this article came out of a discussion with Manuel Oriol, Carlo Furia and Yi Wei. The material is largely theirs but the opinions are mine.)

A paper on automatic testing, submitted some time ago, received the following referee comment:

The case study seems unrealistic and biased toward the proposed technique. 736 unique faults found in 92 classes means at least 8 unique faults per class at the same time. I have never seen in all my life a published library with so many faults …

This would be a good start for a discussion of what is wrong with refereeing in computer science today (on the negativism of our field see [1]); we have a referee who mistakes experience for expertise, prejudice for truth, and refuses to accept carefully documented evidence because “in all his life”, presumably a rich and rewarding life, he has never seen anything of the sort. That is not the focus of the present article, however; arrogant referees eventually retire and good papers eventually get published. The technical problems are what matters. The technical point here is about testing.

Specifically, what bugs are worth finding, and are high bug rates extraordinary?

The paper under review was a step in the work around the automatic testing tool AutoTest (see [2] for a slightly older overall description and [3] for the precise documentation). AutoTest applies a fully automatic strategy, exercising classes and their routines without the need to provide test cases or test oracles. What makes such automation possible is the combination of  random generation of tests and reliance on contracts to determine the success of tests.

For several years we have regularly subjected libraries, in particular the EiffelBase data structure library, to long AutoTest sessions, and we keep finding bugs (the better term is faults). The fault counts are significant; here they caught the referee’s eye. In fact we have had such comments before: I don’t believe your fault counts for production software; your software must be terrible!

Well, maybe.

My guess is that in fact EiffelBase has no more bugs, and possibly far fewer bugs, than other “production” code. The difference is that the  AutoTest framework performs far more exhaustive tests than usually practiced.

This is only a conjecture; unlike the referee I do not claim any special powers that make my guesses self-evident. Until we get test harnesses comparable to AutoTest for environments other than Eiffel and, just as importantly, libraries that are fully equipped with contracts, enabling the detection of bugs that otherwise might not come to light, we will not know whether the explanation is the badness of EiffelBase or the goodness of AutoTest.

What concrete, incontrovertible evidence demonstrates is that systematic random testing does find faults that human testers typically do not. In a 2008 paper [4] with Ilinca Ciupa, Manuel Oriol and Alexander Pretschner, we ran AutoTest on some classes and compared the results with those of human testers (as well as actual bug reports from the field, since this was released software). We found that the two categories are complementary: human testers find faults that are still beyond the reach of automated tools, but they typically never find certain faults that AutoTest, with its stubborn dedication to leaving no stone unturned, routinely uncovers. We keep getting surprised at bugs that AutoTest detects and which no one had sought to test before.

A typical set of cases that human programmers seldom test, but which frequently lead to uncovering bugs, involves boundary values. AutoTest, in its “random-plus” strategy, always exercises special values of every type, such as MAXINT, the maximum representable integer. Programmers don’t. They should — all testing textbooks tell them so — but they just don’t, and perhaps they can’t, as the task is often too tedious for a manual process. It is remarkable how many routines using integers go bezerk when you feed them MAXINT or its negative counterpart. Some of the fault counts that seem so outrageous to our referee directly come from trying such values.

Some would say the cases are so extreme as to be insignificant. Wrong. Many documented software failures and catastrophes are due to untested extreme values. Perhaps the saddest is the case of the Patriot anti-missile system, which at the beginning of the first Gulf war was failing to catch Scud missiles, resulting in one case in the killing of twenty-eight American soldiers in an army barrack. It was traced to a software error [5]. To predict the position of the incoming missile, the computation multiplied time by velocity. The time computation used multiples of the time unit, a tenth of a second, stored in a 24-bit register and hence approximated. After enough time, long enough to elapse on the battlefield, but longer than what the tests had exercised, the accumulated error became so large as to cause a significant — and in the event catastrophic — deviation. The unique poser of automatic testing is that unlike human testers it is not encumbered by a priori notions of a situation being extreme or unlikely. It tries all the possibilities it can.

The following example, less portentous in its consequences but just as instructive, is directly related to AutoTest. For his work on model-based contracts [6] performed as part of his PhD completed in 2008 at ETH, Bernd Schoeller developed classes representing the mathematical notion of set. There were two implementations; it turned out that one of them, say SET1, uses data structures that make the subset operation ⊆ easy to program efficiently; in the corresponding class, the superset operation, a ⊇ b, is then simply implemented as b ⊆ a. In the other implementation, say SET2, it is the other way around: ⊇ is directly implemented, and a ⊆ b, is implemented as b ⊇ a. This all uses a nice object-oriented structure, with a general class SET defining the abstract notion and the two implementations inheriting from it.

Now you may see (if you have developed a hunch for automated testing) where this is heading: AutoTest knows about polymorphism and dynamic binding, and tries all the type combinations that make sense. One of the generated test cases has two variables s1 and s2 of type SET, and tries out s2 ⊆ s1; in one of the combinations that AutoTest tries, s1 is dynamically and polymorphically of type SET1 and s2 of type SET2. The version of ⊆ that it will use is from SET2, so it actually calls s1 ⊇ s2; but this tests the SET1 version of ⊇, which goes back to SET2. The process would go on forever, were it not for a timeout in AutoTest that uncovers the fault. Bernd Schoeller had tried AutoTest on these classes not in the particular expectation of finding bugs, but more as a favor to the then incipient development of AutoTest, to see how well the tool could handle model-based contracts. The uncovering of the fault, testament to the power of relentless, systematic automatic testing, surprised us all.

In this case no contract was violated; the problem was infinite recursion, due to a use of O-O techniques that for all its elegance had failed to notice a pitfall. In most cases, AutoTest finds the faults through violated postconditions or class invariants. This is one more reason to be cautious about sweeping generalizations of the kind “I do not believe these bug rates, no serious software that I have seen shows anything of the sort!”. Contracts express semantic properties of the software, which the designer takes care of stating explicitly. In run-of-the-mill code that does not benefit from such care, lots of things can go wrong but remain undetected during testing, only to cause havoc much later during some actual execution.

When you find such a fault, it is irrelevant that the case is extreme, or special, or rare, or trivial. When a failure happens it no longer matter that the fault was supposed to be rare; and you will only know how harmful it is when you deal with the consequences. Testing, single-mindedly  devoted to the uncovering of faults [7], knows no such distinction: it hunts all bugs large and small.

References

[1] The nastiness problem in computer science, article on the CACM blog, 22 August 2011, available here.

[2] Bertrand Meyer, Ilinca Ciupa, Andreas Leitner, Arno Fiva, Yi Wei and Emmanuel Stapf: Programs that Test Themselves, IEEE Computer, vol. 42, no. 9, pages 46-55, September 2009, also available here.

[3] Online AutoTest documentation, available here at docs.eiffel.com.

[4] Ilinca Ciupa, Bertrand Meyer, Manuel Oriol and Alexander Pretschner: Finding Faults: Manual Testing vs. Random+ Testing vs. User Reports, in ISSRE ’08, Proceedings of the 19th IEEE International Symposium on Software Reliability Engineering, Redmond, November 2008, available here.

[5] US General Accounting Office: GAO Report: Patriot Missile Defense– Software Problem Led to System Failure at Dhahran, Saudi Arabia, February 4, 1992, available here.

[6] Bernd Schoeller, Tobias Widmer and Bertrand Meyer: Making Specifications Complete Through Models, in Architecting Systems with Trustworthy Components, eds. Ralf Reussner, Judith Stafford and Clemens Szyperski, Lecture Notes in Computer Science, Springer-Verlag, 2006, available here.

[7] Bertrand Meyer: Seven Principles of Software testing, in IEEE Computer, vol. 41, no. 10, pages 99-101, August 2008available here.

A safe and stable solution

by

Reading about the latest hullabaloo around Android’s usage of Java, and more generally following the incessant flow of news about X suing Y in the software industry (with many combinations of X and Y) over Java and other object-oriented technologies, someone with an Eiffel perspective can only smile. Throughout its history, suggestions to use Eiffel have often been met initially — along with “Will Eiffel still be around next year?”, becoming truly riotous after 25 years — with objections of proprietariness, apparently because Eiffel initially came from a startup company. In contrast, many other approaches, from C++ to Smalltalk and Java, somehow managed to get favorable vibes from the media; the respective institutions, from AT&T to Xerox and Sun, must be disinterested benefactors of humanity.

Now many who believed this are experiencing a next-morning surprise, discovering under daylight that the person next to whom they wake up is covered with patents and lawsuits.

For their part, people who adopted Eiffel over the years and went on to develop project after project  do not have to stay awake worrying about legal issues and the effects of corporate takeovers; they can instead devote their time to building the best software possible with adequate methods, notations and tools.

This is a good time to recall the regulatory situation of Eiffel. First, the Eiffel Software implementation (EiffelStudio): the product can be used through either an open-source and a proprietary licenses. With both licenses the software is exactly the same; what differs is the status of the code users generate: with the open-source license, they are requested to make their own programs open-source; to keep their code proprietary, they need the commercial license. This is a fair and symmetric requirement. It is made even more attractive by the absence of any run-time fees or royalties of the kind typically charged by database vendors.

The open-source availability of the entire environment, over 2.5 millions line of (mostly Eiffel) code, has spurred the development of countless community contributions, with many more in progress.

Now for the general picture on the language, separate from any particular implementation. Java’s evolution has always been tightly controlled by Sun and now its successor Oracle. There may actually be technical arguments in favor of the designers retaining a strong say in the evolution of a language, but they no longer seem to apply any more now that most of the Java creators have left the company. Contrast this with Eiffel, which is entirely under the control of an international standards committee at ECMA International, the oldest and arguably the most prestigious international standards body for information technology. The standard is freely available online from the ECMA site [1]. It is also an ISO standard [2].

The standardization process is the usual ECMA setup, enabling any interested party to participate. This is not just a statement of principle but the reality, to which I can personally testify since, in spite of being the language’s original designer and author of the reference book, I lost countless battles in the discussions that led to the current standard and continue in preparation of the next version. While I was not always pleased on the moment, the committee’s collegial approach has led to a much more solid result than any single person could have achieved.

The work of ECMA TC49-TG4 (the Eiffel standard committee) has disproved the conventional view that committees can only design camels. In fact TC49-TG4 has constantly worked to keep the language simple and manageable, not hesitating to remove features deemed obsolete or problematic, while extending the range of the language and increasing the Eiffel programmer’s power of expression. As a result, Eiffel today is an immensely better language than when we started our work in 2002. Without a strong community-based process we would never, for example, have made Eiffel the first widespread language to guarantee void-safety (the compile-time removal of null-pointer-dereferencing errors), a breakthrough for software reliability.

Open, fair, free from lawsuits and commercial fights, supported by an enthusiastic community: for projects that need a modern quality-focused software framework, Eiffel is a safe and stable solution.

References

[1] ECMA International: Standard ECMA-367: Eiffel: Analysis, Design and Programming Language, 2nd edition (June 2006), available here (free download).

[2] International Organization for Standardization: ISO/IEC 25436:2006: Information technology — Eiffel: Analysis, Design and Programming Language, available here (for a fee; same text as [1], different formatting).

Reflexivity, and other pillars of civilization

by

Let me start, dear reader of this blog, by probing your view of equality, and also of assignment. Two questions:  

  • Is a value x always equal to itself? (For the seasoned programmers in the audience: I am talking about a value, as in mathematics, not an expression, as in programming, which could have a side effect.)
  • In programming, if we consider an assignment

       x := y

and v is the value of y before that assignment (again, this little detour is to avoid bothering with side effects), is the value of x always equal to v after the assignment?  

Maybe I should include here one of these Web polls that one finds on newspaper sites, so that you can vote and compare your answer to the Wisdom of Crowds. My own vote is clear: yes to both. Equality is reflexive (every value is equal to itself, at any longitude and temperature, no excuses and no exceptions); and the purpose of assignment is to make the value of the target equal to the value of the source. Such properties are some of the last ramparts of civilization. If they go away, what else is left?  

754 enters the picture

Now come floating-point numbers and the famous IEEE “754” floating-point standard [1]. Because not all floating point operations yield a result usable as a floating-point number, the standard introduces a notion of “NaN”, Not a Number; certain operations involving floating-point numbers may yield a NaN. The term NaN does not denote a single value but a set of values, distinguished by their “payloads”.  

Now assume that the value of x is a NaN. If you use a programming language that supports IEEE 754 (as they all do, I think, today) the test in  

        if x = x then …  

is supposed to yield False. Yes, that is specified in the standard: NaN is never equal to NaN (even with the same payload); nor is it equal to anything else; the result of an equality comparison involving NaN will always be False.  

Assignment behavior is consistent with this: if y (a variable, or an expression with no side effect) has a NaN value, then after  

        x := y  

the test x = y will yield False. 

Before commenting further let me note the obvious: I am by no means a numerics expert; I know that IEEE 754 was a tremendous advance, and that it was designed by some of the best minds in the field, headed by Velvel Kahan who received a Turing Award in part for that success. So it is quite possible that I am about to bury myself in piles of ridicule. On the other hand I have also learned that (1) ridicule does not kill, so I am game; and more importantly (2) experts are often right but not always, and it is always proper to question their reasoning. So without fear let me not stop at the arguments that “the committee must have voted on this point and they obviously knew what they were doing” and “it is the standard and implemented on zillions of machines, you cannot change it now”. Both are true enough, but not an excuse to censor questions.  

What are the criteria?

The question is: compatibility with an existing computer standard is great, but what about compatibility with a few hundred years of mathematics? Reflexivity of equality  is something that we expect for any data type, and it seems hard to justify that a value is not equal to itself. As to assignment, what good can it be if it does not make the target equal to the source value?  

The question of assignment is particularly vivid in Eiffel because we express the expected abstract properties of programs in the form of contracts. For example, the following “setter” procedure may have a postcondition (expressed by the ensure clause):  

        set_x (v: REAL)
                        — Set the value of x (an attribute, also of type REAL) the value of v.
                do
                        …
                        x := v  
                ensure
                        x = v
                end  

   
If you call this procedure with a NaN argument for a compiler that applies IEEE 754 semantics, and monitor contracts at run time for testing and debugging, the execution will report a contract violation. This is very difficult for a programmer to accept.  

A typical example arises when you have an assignment to an item of an array of REAL values. Assume you are executing a [i] := x. In an object-oriented view of the world (as in Eiffel), this is considered simplified syntax  for the routine call a.put (x, i). The postcondition is that a [i] = x. It will be violated!  

The experts’ view

I queried a number of experts on the topic. (This is the opportunity to express my gratitude to members of the IFIP working group 2.5 on numerical software [2], some of the world’s top experts in the field, for their willingness to respond quickly and with many insights.) A representative answer, from Stuart Feldman, was:  

If I remember the debate correctly (many moons ago), NaN represents an indefinite value, so there is no reason to believe that the result of one calculation with unclear value should match that of another calculation with unclear value. (Different orders of infinity, different asymptotic approaches toward 0/0, etc.)  

Absolutely correct! Only one little detail, though: this is an argument against using the value True as a result of the test; but it is not an argument for using the value False! The exact same argument can be used to assert that the result should not be False:  

… there is no reason to believe that the result of one calculation with unclear value should not match that of another calculation with unclear value.  

Just as convincing! Both arguments complement each other: there is no compelling reason for demanding that the values be equal; and there is no compelling argument either to demand that they be different. If you ignore one of the two sides, you are biased.  

What do we do then?

The conclusion is not that the result should be False. The rational conclusion is that True and False are both unsatisfactory solutions. The reason is very simple: in a proper theory (I will sketch it below) the result of such a comparison should be some special undefined below; the same way that IEEE 754 extends the set of floating-point numbers with NaN, a satisfactory solution would extend the set of booleans with some NaB (Not a Boolean). But there is no NaB, probably because no one (understandably) wanted to bother, and also because being able to represent a value of type BOOLEAN on a single bit is, if not itself a pillar of civilization, one of the secrets of a happy life.  

If both True and False are unsatisfactory solutions, we should use the one that is the “least” bad, according to some convincing criterion . That is not the attitude that 754 takes; it seems to consider (as illustrated by the justification cited above) that False is somehow less committing than True. But it is not! Stating that something is false is just as much of a commitment as stating that it is true. False is no closer to NaB than True is. A better criterion is: which of the two possibilities is going to be least damaging to time-honored assumptions embedded in mathematics? One of these assumptions is the reflexivity of equality:  come rain or shine, x is equal to itself. Its counterpart for programming is that after an assignment the target will be equal to the original value of the source. This applies to numbers, and it applies to a NaN as well. 

Note that this argument does not address equality between different NaNs. The standard as it is states that a specific NaN, with a specific payload, is not equal to itself.  

What do you think?

A few of us who had to examine the issue recently think that — whatever the standard says at the machine level — a programming language should support the venerable properties that equality is reflexive and that assignment yields equality.

Every programming language should decide this on its own; for Eiffel we think this should be the specification. Do you agree?  

Some theory

For readers who like theory, here is a mathematical restatement of the observations above. There is nothing fundamentally new in this section, so if you do not like strange symbols you can stop here.  

The math helps explain the earlier observation that neither True nor False is more“committing” than the other. A standard technique (coming from denotational semantics) for dealing with undefinedness in basic data types, is to extend every data type into a lattice, with a partial order relation meaning “less defined than”. The lattice includes a bottom element, traditionally written “⊥” (pronounced “Bottom”) and a top element written ⊤ (“Top”). ⊥ represents an unknown value (not enough information) and ⊤ an error value (too much information). Pictorially, the lattice for natural numbers would look like this:  

Integer lattice
The lattice of integers

On basic types, we always use very simple lattices of this form, with three kinds of element: ⊥, less than every other element; ⊤, larger than all other elements; and in-between all the normal values of the type, which for the partial order of interest are all equal. (No, this is not a new math in which all integers are equal. The order in question simply means “is less defined than”. Every integer is as defined as all other integers, more defined than ⊥, and less defined than ⊤.) Such lattices are not very exciting, but they serve as a starting point; lattices with more interesting structures are those applying to functions on such spaces — including functions of functions —, which represent programs.  

The modeling of floating-point numbers with NaN involves such a lattice; introducing NaN means introducing a ⊥ value. (Actually, one might prefer to interpret NaN as ⊤, but the reasoning transposes immediately.)  More accurately, since there are many NaN values, the lattice will look more like this:

Float lattice
The lattice of floats in IEEE 754

For simplicity we can ignore the variety of NaNs and consider a single ⊤.

Functions on lattices — as implemented by programs — should satisfy a fundamental property: monotonicity. A function f  is monotone (as in ordinary analysis) if, whenever x ≤ y, then f (x) ≤ f (y). Monotonicity is a common-sense requirement: we cannot get more information from less information. If we know less about x than about y, we cannot expect that any function (with a computer, any program) f will, out of nowhere, restore the missing information.  

Demanding monotonicity of all floating-point operations reflects this exigency of monotonicity: indeed, in IEEE 754, any arithmetic operation — addition, multiplication … — that has a NaN as one of its arguments must yield a Nan as its result. Great. Now for soundness we should also have such a property for boolean-valued operations, such as equality. If we had a NaB as the ⊥ of booleans, just like NaN is the ⊥ of floating-point numbers,  then the result of NaN = NaN would be NaB. But the world is not perfect and the IEEE 754 standard does not govern booleans. Somehow (I think) the designers thought of False as somehow less defined than True. But it is not! False is just as defined as True in the very simple lattice of booleans; according to the partial order, True and False are equal for the relevant partial order:

Boolean lattice
The lattice of booleans

Because any solution that cannot use a NaB will violate monotonicity and hence will be imperfect, we must resort to heuristic criteria. A very strong criterion in favor of choosing True is reflexivity — remaining compatible with a fundamental property of equality. I do not know of any argument for choosing False. 

The Spartan approach

There is, by the way, a technique that accepts booleans as we love them (with two values and no NaB) and achieves mathematical rigor. If operations involving NaNs  truly give us pimples, we can make any such operation trigger an exception. In the absence of ⊥ values,  this is an acceptable programming technique for representing undefinedness. The downside, of course, is that just about everywhere the program must be ready to handle the exception in some way. 

It is unlikely that in practice many people would be comfortable with such a solution. 

Final observations

Let me point out two objections that I have seen. Van Snyder wrote: 

NaN is not part of the set of floating-point numbers, so it doesn’t behave as if “bottom” were added to the set. 

Interesting point, but, in my opinion not applicable: ⊥ is indeed not part of the mathematical set of floating point numbers, but in the form of NaN it is part of the corresponding type (float in C, REAL in Eiffel); and the operations of the type are applicable to all values, including NaN if, as noted, we have not taken the extreme step of triggering an exception every time an operation uses a NaN as one of its operands. So we cannot free ourselves from the monotonicity concern by just a sleight of hands. 

Another comment, also by Van Snyder (slightly abridged): 

Think of [the status of NaN] as a variety of dynamic run-time typing. With static typing, if  x is an integer variable and y

        x := y 

does not inevitably lead to 

        x = y

 True; and a compelling argument to require that conversions satisfy equality as a postcondition! Such  reasoning — reflexivity again — was essential in the design of the Eiffel conversion mechanism [3], which makes it possible to define conversions between various data types (not just integers and reals and the other classical examples, but also any other user types as long as the conversion does not conflict with inheritance). The same conversion rules apply to assignment and equality, so that yes, whenever the assignment x := y is permitted, including when it involves a conversion, the property x = y  is afterwards always guaranteed to hold.

It is rather dangerous indeed to depart from the fundamental laws of mathematics. 

References

[1] IEEE floating-point standard, 754-2008; see summary and references in the Wikipedia entry.  

[2] IFIP Working Group 2.5 on numerical software: home page. 

[3] Eiffel standard (ECMA and ISO), available on the ECMA site.

A couple of loop examples

by

(This entry originated as a post on the EiffelStudio user group mailing list.) 

Here are a couple of actual examples of the new loop variants discussed in the blog entry immediately preceding this one. They came out of my current work; I started updating a program to take advantage of the new facility.

As a typical example, I replaced

        local
                eht: HASH_TABLE [EXPRESSION, EXPRESSION]
        do
                …
        from
                eht := item (e)
                eht.start
         until
                eht.off
        loop
                Result.extend (eht.key_for_iteration)
                eht.forth
        end 

 by

        across item (e) as eht loop Result.extend (eht.key) end

 which also gets rid of the local variable declaration. The second form is syntactic sugar for the first, but I find it justified. 

 Another case, involving nested loops: 

— Previously:

        from
                other.start
        until
                other.off
        loop
                oht := other.item_for_iteration
                e := other.key_for_iteration
                from
                        oht.start
                until
                        oht.off
                loop
                        put (e, oht.item_for_iteration)
                        oht.forth
                end
                other.forth
        end

— Now:

        across other as o loop
                across o.item as oht loop put (o.key, oht.item) end
        end

here getting rid of two local variable declarations (although I might for efficiency reintroduce the variable e  to compute o.key just once). 

It is important to note that these are not your grandmother’s typical loops: they iterate on complex data structures, specifically hash tables where the keys are lists and the items are themselves hash tables, with lists as both items and keys. 

The mechanism is applicable to all the relevant data structures in EiffelBase (in other words, no need for the programmer to modify anything, just apply the across  loop to any such structure), and can easily extended to any new structure that one wishes to define. In the short term at least, I still plan in my introductory teaching to show the explicit variants first, as it is important for beginners to understand how a loop works. (My hunch based on previous cases is that after a while we will feel comfortable introducing the abstract variants from the start, but it takes some time to learn how to do it right.)

More expressive loops for Eiffel

by

New variants of the loop construct have been introduced into Eiffel, allowing a safer, more concise and more abstract style of programming. The challenge was to remain compatible with the basic loop concept, in particular correctness concerns (loop invariant and loop variant), to provide a flexible mechanism that would cover many different cases of iteration, and to keep things simple.

Here are some examples of the new forms. Consider a structure s, such as a list, which can be traversed in sequence. The following loop prints all elements of the list:

      across s as c loop print (c.item) end

(The procedure print is available on all types, and can be adapted to any of them by redefining the out feature; item gives access to individual values of the list.) More about c in just a moment; in the meantime you can just consider consider that using “as c” and manipulating the structure through c rather than directly through s  is a simple idiom to be learned and applied systematically for such across loops.

The above example is an instruction. The all and some variants yield boolean expressions, as in

across s as c all c.item > 0 end

which denotes a boolean value, true if and only if all elements of the list are positive. To find out if at least one is positive, use

across s as c some c.item > 0 end

Such expressions could appear, for example, in a class invariant, but they may be useful in many different contexts.

In some cases, a from clause is useful, as in

        across s as c from sum := 0  loop sum := sum + c.index ∗ c.item end
— Computes Σ i * s [i]

The original form of loop in Eiffel is more explicit, and remains available; you can achieve the equivalent of the last example, on a suitable structure, as

A list and a cursor
A list and a cursor

      from
sum := 0 ; s.start
until
s.after
loop
sum := sum + s.index ∗ s.item
s.forth
        end

which directly manipulates a cursor through s, using start to move it to the beginning, forth to advance it, and after to test if it is past the last element. The forms with across achieve the same purpose in a more concise manner. More important than concision is abstraction: you do not need to worry about manipulating the cursor through start, forth and after. Under the hood, however, the effect is the same. More precisely, it is the same as in a loop of the form

from
sum := 0 ; c.start
until
c.after
loop
sum := sum + c.index ∗ c.item
c.forth
        end

where c is a cursor object associated with the loop. The advantage of using a cursor is clear: rather than keeping the state of the iteration in the object itself, you make it external, part of a cursor object that, so to speak, looks at the list. This means in particular that many traversals can be active on the same structure at the same time; with an internal cursor, they would mess up with each other, unless you manually took the trouble to save and restore cursor positions. With an external cursor, each traversal has its own cursor object, and so does not interfere with other traversals — at least as long as they don’t change the structure (I’ll come back to that point).

With the across variant, you automatically use a cursor; you do not have to declare or create it: it simply comes as a result of the “as c” part of the construct, which introduces c as the cursor.

On what structures can you perform such iterations? There is no limitation; you simply need a type based on a class that inherits, directly or indirectly, from the library class ITERABLE. All relevant classes from the EiffelBase library have been updated to provide this inheritance, so that you can apply the across scheme to lists of all kinds, hash tables, arrays, intervals etc.

One of these structures is the integer interval. The notation  m |..| n, for integers m and n, denotes the corresponding integer interval. (This is not a special language notation, simply an operator, |..|, defined with the general operator mechanism as an alias for the feature interval of INTEGER classes.) To iterate on such an interval, use the same form as in the examples above:

        across m |..| n  as c from sum := 0  loop sum := sum + a [c.item] end
— Computes Σ a [i], for i ranging from m to n, for an array (or other structure) a. 

The key feature in ITERABLE is new_cursor, which returns a freshly created cursor object associated with the current structure. By default it is an ITERATION_CURSOR, the most general cursor type, but every descendant of ITERABLE can redefine the result type to something more specific to the current structure. Using a cursor — c in the above examples —, rather than manipulating the structure s directly, provides considerable flexibility thanks to the property that ITERATION_CURSOR itself inherits from ITERABLE   and hence has all the iteration mechanisms. For example you may write

across s.new_cursor.reversed as c loop print (c.item) end

to print elements in reverse order. (Using Eiffel’s operator  mechanism, you may write – s.new_cursor, with a minus operator, as a synonym for new_cursor.reversed.) The function reversed gives you a new cursor on the same target structure, enabling you to iterate backwards. Or you can use

        across s.new_cursor + 3 as c loop print (c.item) end

(using s.new_cursor.incremented (3) rather than s.new_cursor + 3 if you are not too keen on operator syntax) to iterate over every third item. A number of other possibilities are available in the cursor classes.

A high-level iteration mechanism is only safe if you have the guarantee that the structure remains intact throughout the iteration. Assume you are iterating through a structure

across s   as c loop some_routine end

and some_routine changes the structure s: the whole process could be messed up. Thanks to Design by Contract mechanisms, the library protects you against such mistakes. Features such as item and index, accessing properties of the structure during the iteration, are equipped with a precondition clause

require
is_valid

and every operation that changes the structure sets is_valid to false. So as soon as any change happens, you cannot continue the iteration; all you can do is restart a new one; the command start, used internally to start the operation, does not have the above precondition.

Sometimes, of course, you do want to change a structure while traversing it; for example you may want to add an element just to the right of the iteration position. If you know what you are doing that’s fine. (Let me correct this: if you know what you are doing, express it through precise contracts, and you’ll be fine.) But then you should not use the abstract forms of the loop, across…; you should control the iteration itself through the basic form from … until … with explicit cursor manipulation, protected by appropriate contracts.

The two styles, by the way, are not distinct constructs. Eiffel has always had only one form of loop and this continues the case. The across forms are simply new possibilities added to the classical loop construct, with obvious constraints stating for example that you may not have both a some or all form and an explicit  loop body.  In particular, an across loop can still have an invariant clause , specifying the correctness properties of the loop, as in

        across s as c from sum := 0  invariant sum = sigma (s, index)  loop sum := sum + c.index ∗ c.item end

EiffelStudio 6.5 already included the language update; the library update (not yet including the is_valid preconditions for data structure classes) will be made available this week.

These new mechanisms should increase the level of abstraction and the reliability of loops, a fundamental element of  almost all programs.

The theory and calculus of aliasing

by

In a previous post I briefly mentioned some work that I am doing on aliasing. There is a draft paper [1], describing the theory, calculus, graphical notation (alias diagrams) and implementation. Here I will try to give an idea of what it’s about, with the hope that you will be intrigued enough to read the article. Even before you read it you might try out the implementation[2], a simple interactive interface with all the examples of the article .

What the article does not describe in detail — that will be for a companion paper— is how the calculus will be used as part of a general framework for developing object-oriented software proved correct from the start, the focus of our overall  “Trusted Components” project’ [3]. Let me simply state that the computation of aliases is the key missing step in the effort to make correctness proofs a standard part of software development. This is a strong claim which requires some elaboration, but not here.

The alias calculus asks a simple question: given two expressions representing references (pointers),  can their values, at a given point in the program, ever reference the same object during execution?

As an example  application, consider two linked lists x and y, which can be manipulated with operations such as extend, which creates a new cell and adds it at the end of the list:

lists

 The calculus makes it possible to prove that if  x and y are not aliased to each other, then none of the pointers in any of the cells in either of the lists can point to  (be aliased to) any cell of  the other. If  x is initially aliased to y, the property no longer holds. You can run the proof (examples 18 and 19) in the downloadable implementation.

The calculus gives a set of rules, each applying to a particular construct of the language, and listed below.

The rule for a construct p is of the form

          a |= p      =   a’ 

where a and a’ are alias relations; this states that executing p  in a state where the alias relation is a will yield the alias relation a’ in the resulting state. An alias relation is a symmetric, irreflexive relation; it indicates which expressions and variables can be aliased to each other in a given state.

The constructs p considered in the discussion are those of a simplified programming language; a modern object-oriented language such as Eiffel can easily be translated into that language. Some precision will be lost in the process, meaning that the alias calculus (itself precise) can find aliases that would not exist in the original program; if this prevents proofs of desired properties, the cut instruction discussed below serves to correct the problem.

The first rule is for the forget instruction (Eiffel: x := Void):

          a |= forget x       =   a \- {x}

where the \- operator removes from a relation all the elements belonging to a given set A. In the case of object-oriented programming, with multidot expressions x.y.z, the application of this rule must remove all elements whose first component, here x, belongs to A.

The rule for creation is the same as for forget:

         a |= create x          =   a \- {x}

The two instructions have different semantics, but the same effect on aliasing.

The calculus has a rule for the cut instruction, which removes the connection between two expressions:

        a |= cut x, y       =   a — <x, y>

where — is set difference and <x, y> includes the pairs [x, y] and [y, x] (this is a special case of a general notation defined in the article, using the overline symbol). The cut   instruction corresponds, in Eiffel, to cut   x /= y end:  a hint given to the alias calculus (and proved through some other means, such as standard axiomatic semantics) that some references will not be aliased.

The rule for assignment is

      a |= (x := y)      =   given  b = a \- {x}   then   <b È {x} x (b / y)}> end

where b /y (“quotient”), similar to an equivalence class in an equivalence relation, is the set of elements aliased to y in b, plus y itself (remember that the relation is irreflexive). This rule works well for object-oriented programming thanks to the definition of the \- operator: in x := x.y, we must not alias x to x.y, although we must alias it to any z that was aliased to x.y.

The paper introduces a graphical notation, alias diagrams, which makes it possible to reason effectively about such situations. Here for example is a diagram illustrating the last comment:

Alias diagram for a multidot assignment
Alias diagram for a multidot assignment

(The grayed elements are for explanation and not part of the final alias relation.)

For the compound instruction, the rule is:

           a |= (p ;  q)      =   (a |= p) |= q)

For the conditional instruction, we get:

           a |= (then p else  q end)      =   (a |= p) È  (a |= q)

Note the form of the instruction: the alias calculus ignores information from the then clause present in the source language. The union operator is the reason why  alias relations,  irreflexive and symmetric, are not  necessarily transitive.

The loop instruction, which also ignores the test (exit or continuation condition), is governed by the following rule:

           a |= (loop p end)       =   tN

where span style=”color: #0000ff;”>N is the first value such that tN = tN+1 (in other words, tN is the fixpoint) in the following sequence:

            t0          =    a
           tn+1       =   (tn È (tn |= p))     

The existence of a fixpoint and the correctness of this formula to compute it are the result of a theorem in the paper, the “loop aliasing theorem”; the proof is surprisingly elaborate (maybe I missed a simpler one).

For procedures, the rule is

         a |= call p        =   a |= p.body

where p.body is the body of the procedure. In the presence of recursion, this gives rise to a set of equations, whose solution is the fixpoint; again a theorem is needed to demonstrate that the fixpoint exists. The implementation directly applies fixpoint computation (see examples 11 to 13 in the paper and implementation).

The calculus does not directly consider routine arguments but treats them as attributes of the corresponding class; so a call is considered to start with assignments of the form f : = a for every pair of formal and actual arguments f and a. Like the omission of conditions in loops and conditionals, this is a source of possible imprecision in translating from an actual programming language into the calculus, since values passed to recursive activations of the same routine will be conflated.

Particularly interesting is the last rule, which generalizes the previous one to qualified calls of the form x. f (…)  as they exist in object-oriented programming. The rule involves the new notion of inverse variable, written x’ where x is a variable. Laws of the calculus (with Current denoting the current object, one of the fundamental notions of object-oriented programming) are

        Current.x            = x   
        x.Current            = x
        x.x’                      = Current
        x’.x                      = Current

In other words, Current plays the role of zero element for the dot operator, and variable inversion is the inverse operation. In a call x.f, where x denotes the supplier object (the target of the call), the inverse variable provides a back reference to the client object (the caller), indispensable to interpret references in the original context. This property is reflected by the qualified client rule, which uses  the auxiliary operator n (where x n a, for a relation a and a variable x, is the set of pairs [x.u, y.v] such that the pair [u, v] is in a). The rule is:

         a |= call x.r       =   x n ((x’ n a ) |= call r)

You need to read the article for the full explanation, but let me offer the following quote from the corresponding section (maybe you will note a familiar turn of phrase):

Thus we are permitted to prove that the unqualified call creates certain aliasings, on the assumption that it starts in its own alias environment but has access to the caller’s environment through the inverted variable, and then to assert categorically that the qualified call has the same aliasings transposed back to the original environment. This change of environment to prove the unqualified property, followed by a change back to the original environment to prove the qualified property, explains well the aura of magic which attends a programmer’s first introduction to object-oriented programming.

I hope you will enjoy the calculus and try the examples in the implementation. It is fun to apply, and there seems to be no end to the potential applications.

Reference

[1] Bertrand Meyer: The Theory and Calculus of Aliasing, draft paper, first published 12 January 2009 (revised 21 January 2010), available here and also at arxiv.org.
[2] Implementation (interactive version to try all the examples of the paper): downloadable Windows executable here.
[3] Bertrand Meyer: The Grand Challenge of Trusted Components, in 2003 International Conference on Software Engineering, available here.