Reflexivity, and other pillars of civilization
Let me start, dear reader of this blog, by probing your view of equality, and also of assignment. Two questions:
- Is a value x always equal to itself? (For the seasoned programmers in the audience: I am talking about a value, as in mathematics, not an expression, as in programming, which could have a side effect.)
- In programming, if we consider an assignment
x := y
and v is the value of y before that assignment (again, this little detour is to avoid bothering with side effects), is the value of x always equal to v after the assignment?
Maybe I should include here one of these Web polls that one finds on newspaper sites, so that you can vote and compare your answer to the Wisdom of Crowds. My own vote is clear: yes to both. Equality is reflexive (every value is equal to itself, at any longitude and temperature, no excuses and no exceptions); and the purpose of assignment is to make the value of the target equal to the value of the source. Such properties are some of the last ramparts of civilization. If they go away, what else is left?
754 enters the picture
Now come floating-point numbers and the famous IEEE “754” floating-point standard [1]. Because not all floating point operations yield a result usable as a floating-point number, the standard introduces a notion of “NaN”, Not a Number; certain operations involving floating-point numbers may yield a NaN. The term NaN does not denote a single value but a set of values, distinguished by their “payloads”.
Now assume that the value of x is a NaN. If you use a programming language that supports IEEE 754 (as they all do, I think, today) the test in
if x = x then …
is supposed to yield False. Yes, that is specified in the standard: NaN is never equal to NaN (even with the same payload); nor is it equal to anything else; the result of an equality comparison involving NaN will always be False.
Assignment behavior is consistent with this: if y (a variable, or an expression with no side effect) has a NaN value, then after
x := y
the test x = y will yield False.
Before commenting further let me note the obvious: I am by no means a numerics expert; I know that IEEE 754 was a tremendous advance, and that it was designed by some of the best minds in the field, headed by Velvel Kahan who received a Turing Award in part for that success. So it is quite possible that I am about to bury myself in piles of ridicule. On the other hand I have also learned that (1) ridicule does not kill, so I am game; and more importantly (2) experts are often right but not always, and it is always proper to question their reasoning. So without fear let me not stop at the arguments that “the committee must have voted on this point and they obviously knew what they were doing” and “it is the standard and implemented on zillions of machines, you cannot change it now”. Both are true enough, but not an excuse to censor questions.
What are the criteria?
The question is: compatibility with an existing computer standard is great, but what about compatibility with a few hundred years of mathematics? Reflexivity of equality is something that we expect for any data type, and it seems hard to justify that a value is not equal to itself. As to assignment, what good can it be if it does not make the target equal to the source value?
The question of assignment is particularly vivid in Eiffel because we express the expected abstract properties of programs in the form of contracts. For example, the following “setter” procedure may have a postcondition (expressed by the ensure clause):
set_x (v: REAL)
— Set the value of x (an attribute, also of type REAL) the value of v.
do
…
x := v
ensure
x = v
end
If you call this procedure with a NaN argument for a compiler that applies IEEE 754 semantics, and monitor contracts at run time for testing and debugging, the execution will report a contract violation. This is very difficult for a programmer to accept.
A typical example arises when you have an assignment to an item of an array of REAL values. Assume you are executing a [i] := x. In an object-oriented view of the world (as in Eiffel), this is considered simplified syntax for the routine call a.put (x, i). The postcondition is that a [i] = x. It will be violated!
The experts’ view
I queried a number of experts on the topic. (This is the opportunity to express my gratitude to members of the IFIP working group 2.5 on numerical software [2], some of the world’s top experts in the field, for their willingness to respond quickly and with many insights.) A representative answer, from Stuart Feldman, was:
If I remember the debate correctly (many moons ago), NaN represents an indefinite value, so there is no reason to believe that the result of one calculation with unclear value should match that of another calculation with unclear value. (Different orders of infinity, different asymptotic approaches toward 0/0, etc.)
Absolutely correct! Only one little detail, though: this is an argument against using the value True as a result of the test; but it is not an argument for using the value False! The exact same argument can be used to assert that the result should not be False:
… there is no reason to believe that the result of one calculation with unclear value should not match that of another calculation with unclear value.
Just as convincing! Both arguments complement each other: there is no compelling reason for demanding that the values be equal; and there is no compelling argument either to demand that they be different. If you ignore one of the two sides, you are biased.
What do we do then?
The conclusion is not that the result should be False. The rational conclusion is that True and False are both unsatisfactory solutions. The reason is very simple: in a proper theory (I will sketch it below) the result of such a comparison should be some special undefined below; the same way that IEEE 754 extends the set of floating-point numbers with NaN, a satisfactory solution would extend the set of booleans with some NaB (Not a Boolean). But there is no NaB, probably because no one (understandably) wanted to bother, and also because being able to represent a value of type BOOLEAN on a single bit is, if not itself a pillar of civilization, one of the secrets of a happy life.
If both True and False are unsatisfactory solutions, we should use the one that is the “least” bad, according to some convincing criterion . That is not the attitude that 754 takes; it seems to consider (as illustrated by the justification cited above) that False is somehow less committing than True. But it is not! Stating that something is false is just as much of a commitment as stating that it is true. False is no closer to NaB than True is. A better criterion is: which of the two possibilities is going to be least damaging to time-honored assumptions embedded in mathematics? One of these assumptions is the reflexivity of equality: come rain or shine, x is equal to itself. Its counterpart for programming is that after an assignment the target will be equal to the original value of the source. This applies to numbers, and it applies to a NaN as well.
Note that this argument does not address equality between different NaNs. The standard as it is states that a specific NaN, with a specific payload, is not equal to itself.
What do you think?
A few of us who had to examine the issue recently think that — whatever the standard says at the machine level — a programming language should support the venerable properties that equality is reflexive and that assignment yields equality.
Every programming language should decide this on its own; for Eiffel we think this should be the specification. Do you agree?
Some theory
For readers who like theory, here is a mathematical restatement of the observations above. There is nothing fundamentally new in this section, so if you do not like strange symbols you can stop here.
The math helps explain the earlier observation that neither True nor False is more“committing” than the other. A standard technique (coming from denotational semantics) for dealing with undefinedness in basic data types, is to extend every data type into a lattice, with a partial order relation meaning “less defined than”. The lattice includes a bottom element, traditionally written “⊥” (pronounced “Bottom”) and a top element written ⊤ (“Top”). ⊥ represents an unknown value (not enough information) and ⊤ an error value (too much information). Pictorially, the lattice for natural numbers would look like this:
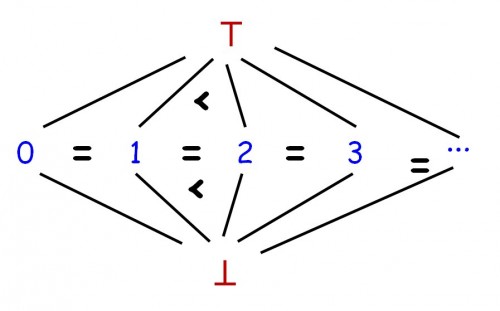
The lattice of integers
On basic types, we always use very simple lattices of this form, with three kinds of element: ⊥, less than every other element; ⊤, larger than all other elements; and in-between all the normal values of the type, which for the partial order of interest are all equal. (No, this is not a new math in which all integers are equal. The order in question simply means “is less defined than”. Every integer is as defined as all other integers, more defined than ⊥, and less defined than ⊤.) Such lattices are not very exciting, but they serve as a starting point; lattices with more interesting structures are those applying to functions on such spaces — including functions of functions —, which represent programs.
The modeling of floating-point numbers with NaN involves such a lattice; introducing NaN means introducing a ⊥ value. (Actually, one might prefer to interpret NaN as ⊤, but the reasoning transposes immediately.) More accurately, since there are many NaN values, the lattice will look more like this:
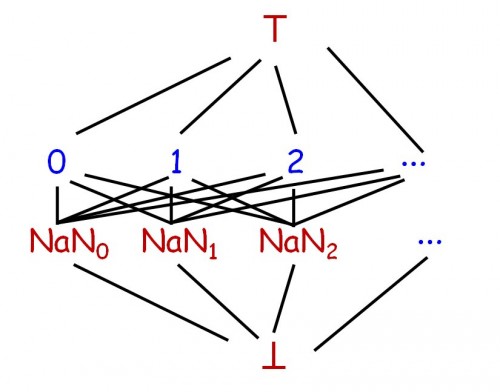
The lattice of floats in IEEE 754
For simplicity we can ignore the variety of NaNs and consider a single ⊤.
Functions on lattices — as implemented by programs — should satisfy a fundamental property: monotonicity. A function f is monotone (as in ordinary analysis) if, whenever x ≤ y, then f (x) ≤ f (y). Monotonicity is a common-sense requirement: we cannot get more information from less information. If we know less about x than about y, we cannot expect that any function (with a computer, any program) f will, out of nowhere, restore the missing information.
Demanding monotonicity of all floating-point operations reflects this exigency of monotonicity: indeed, in IEEE 754, any arithmetic operation — addition, multiplication … — that has a NaN as one of its arguments must yield a Nan as its result. Great. Now for soundness we should also have such a property for boolean-valued operations, such as equality. If we had a NaB as the ⊥ of booleans, just like NaN is the ⊥ of floating-point numbers, then the result of NaN = NaN would be NaB. But the world is not perfect and the IEEE 754 standard does not govern booleans. Somehow (I think) the designers thought of False as somehow less defined than True. But it is not! False is just as defined as True in the very simple lattice of booleans; according to the partial order, True and False are equal for the relevant partial order:
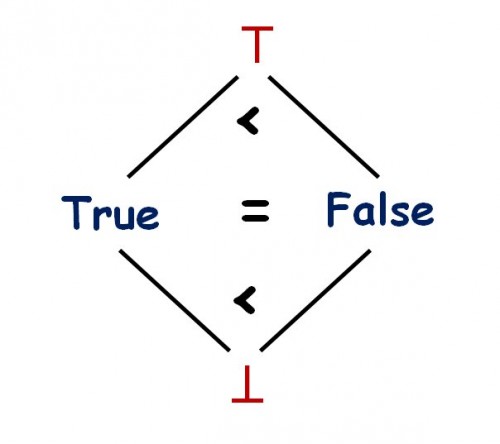
The lattice of booleans
Because any solution that cannot use a NaB will violate monotonicity and hence will be imperfect, we must resort to heuristic criteria. A very strong criterion in favor of choosing True is reflexivity — remaining compatible with a fundamental property of equality. I do not know of any argument for choosing False.
The Spartan approach
There is, by the way, a technique that accepts booleans as we love them (with two values and no NaB) and achieves mathematical rigor. If operations involving NaNs truly give us pimples, we can make any such operation trigger an exception. In the absence of ⊥ values, this is an acceptable programming technique for representing undefinedness. The downside, of course, is that just about everywhere the program must be ready to handle the exception in some way.
It is unlikely that in practice many people would be comfortable with such a solution.
Final observations
Let me point out two objections that I have seen. Van Snyder wrote:
NaN is not part of the set of floating-point numbers, so it doesn’t behave as if “bottom” were added to the set.
Interesting point, but, in my opinion not applicable: ⊥ is indeed not part of the mathematical set of floating point numbers, but in the form of NaN it is part of the corresponding type (float in C, REAL in Eiffel); and the operations of the type are applicable to all values, including NaN if, as noted, we have not taken the extreme step of triggering an exception every time an operation uses a NaN as one of its operands. So we cannot free ourselves from the monotonicity concern by just a sleight of hands.
Another comment, also by Van Snyder (slightly abridged):
Think of [the status of NaN] as a variety of dynamic run-time typing. With static typing, if x is an integer variable and y
x := y
does not inevitably lead to
x = y
True; and a compelling argument to require that conversions satisfy equality as a postcondition! Such reasoning — reflexivity again — was essential in the design of the Eiffel conversion mechanism [3], which makes it possible to define conversions between various data types (not just integers and reals and the other classical examples, but also any other user types as long as the conversion does not conflict with inheritance). The same conversion rules apply to assignment and equality, so that yes, whenever the assignment x := y is permitted, including when it involves a conversion, the property x = y is afterwards always guaranteed to hold.
It is rather dangerous indeed to depart from the fundamental laws of mathematics.
References
[1] IEEE floating-point standard, 754-2008; see summary and references in the Wikipedia entry.
[2] IFIP Working Group 2.5 on numerical software: home page.
[3] Eiffel standard (ECMA and ISO), available on the ECMA site.




 Informatics Europe
Informatics Europe LASER summer school
LASER summer school Propulsion Academy
Propulsion Academy
ISTM that either three-valued logic (i.e. SQL TRUE, FALSE and NULL behaviour) or signalling NaNs are preferable to silent NaNs. Signalling NaNs by default are preferable for practical reasons too; usually a NaN is caused by a programming mistake where an argument to an operation wasn’t correctly bounds-checked.
Of course, floating-point numbers are imperfect substitutes for mathematical real-valued numbers – I think REAL is a poor choice of name for the type in a programming language, as it has the potential to mislead the mathematically minded – since many functions on floating-point values that a mathematician would expect to be identity functions will turn out to accumulate imprecision, resulting in similarly surprising x != x.
This article is great and summarizes the problems with 754 very nicely.
Math is partial and there are different ways to handle this. Problems show when these ways are mixed, for example through the interactions between Boolean and Real.
One way is the use of NaN and any other 3-valued logic. But then, Boolean value should have a NaB. Another is the use of preconditions. That is what Eiffel uses. To be consistent, Eiffel should raise a precondition violation whenever an operation would produce a NaN.
I think that regardless of whether you opt for NaN=NaN or NaN/=NaN there is good mathematics to back your decision. The full mathematical story is in any case much more complicated than what is captured by NaN’s, and the responsibility for using them correctly must ultimately rest with the programmer.
If a1, a2, … and b1, b2, … are sequences of real numbers that both approach 0, then the sequence of quotients a1/b1, a2/b2, … in general will not approach any real number, but will rather have a set of (extended) real numbers as its limit (the smallest of which is known as the inferior limit and the largest of which is known as the superior limit).
We can adopt the convention that an ordinary function applied to a set is equal to the set of function values, and we can then go on to calculate with sets of real numbers much as with real numbers (the first person to do this may have been Weierstrass). Let us now consider the question of equality between such sets. We know that {3, 4} and {4, 7} are different by ordinary set equality, but if we apply the equality function to the pairs (3, 4), (3, 7), (4, 4), and (4, 7) then the results will be False, False, True, and False, respectively, giving us the set {False, True}. In fact, we get the same result if we compare {3, 4} to itself.
How are we to interpret an equality that evaluates to {False, True}? If we interpret it as True then transitivity of equality will quickly lead to all real numbers allegedly being one and the same thing. I would say that what this really means is that there is a not-too-unnatural sense in which all real numbers are _equivalent_. If we interpret {False, True} as being False, then we allegedly have things/objects/entities which are not equal to themselves (or maybe I should say that we have a single thing/object/entity which is not equal to itself – without equality we have no standard for counting things.). Finally, we may prefer to restrict the domain of definition of our equality relation so that the cases that gave {False, True} are excluded from consideration.
Based on these three possibilities one might conclude that we cannot have NaN=NaN without getting x=y for any real numbers x and y (thus vindicating IEEE 754). However, we also have the set equality that makes {3, 4} distinct from {4, 7}, and we can use this type of equality to introduce yet another type of equality: We may consider all sets that contain more than one real number to be one and the same object, and we may call this object “NaN”. In fact, there is mathematical research that supports treating NaN as a first-class object: See http://en.wikipedia.org/wiki/Wheel_theory .
I think there are many topics related to this post and I’ll try to summarize what each of them led me to think.
1. I don’t have access to the standard as it seems the reference document is not free of charge. Why you must pay to know the standard is one topic but I’ll leave it for another time. Wikipedia has a link to a recent draft (1.2.9) and I believe you’re refering to section 7.11 that I will quote here:
“Comparisons are exact and never overflow or underflow. Four mutually exclusive relations are possible: less
than, equal, greater than, and unordered. The last case arises when at least one operand is NaN. Every NaN
shall compare unordered with everything, including itself. Comparisons shall ignore the sign of zero
(so +0 = −0). Infinite operands of the same sign shall compare equal.
Languages define how the result of a comparison shall be delivered, in one of two ways: either as a condition
code identifying one of the four relations listed above, or as a true-false response to a predicate that names the
specific comparison desired.”
I didn’t see anything else in this draft specifying that NaN comparison should yield false, however “Every NaN
shall compare unordered with everything, including itself” leaves no doubt about that since unordered is not equal.
Note that raising an exception would violate the standard, I believe, since comparing two numbers even if one is a NaN is a non-signaling operation.
2. I think the problem is that we want to maintain not two properties (equality is reflexive, and NaN /= NaN) but three, the third being that all objects can be compared. This is captured by the fact that is_equal is a feature of ANY, while other comparison features such as is_less come from specialized classes like COMPARABLE.
In a world with is_equal being a feature of an abstract class (EQUATABLE? It sounds ugly) the REAL class would not inherit this feature. Real numbers could not be compared with is_equal. They would be compared with a dedicated feature taking one of “less than”, “equal”, “greater than” and “unordered” as an argument, that could then safely return true or false as specified by the standard.
3. I’ve been confronted in the past with problems such as this one. Almost always, it comes from trying to mix orange and apples in a single value or concept. The way out is then to clearly separate the involved values and concepts in different entities. For instance, consider this definition of REAL:
class REAL
…
feature
value: ARRAY[INTEGER_8] — The numeric value
meaningful: BOOLEAN — False if a NaN
…
end
Then the value of a number is separate from the boolean attribute that indicates if it has a meaning. The proper redefinition of is_equal becomes
is_equal (other: like Current): BOOLEAN
do
if meaningful and other.meaningful then
result := value.is_equal(other.value)
else
result := False
end
end
This definition satisfies x /= x when x.meaningful is False.
4. You could argue that this is only an artificial trick to reconcile Eiffel contracts and the IEEE standard. I think it goes deeper than that. Equality in Eiffel, and probably all languages, is only an approximation of mathematical equality. If you asked, during a math course “does x = x?” then sure I’d answer yes. But during a computing course? I’d answer “depends…”. Many aspects of computer languages are traductions of mathematical operations and properties that want to stay as close as the original concept, but never succeed that it.
There are well known examples. Take this function for instance:
identity_with_a_trick (n: INTEGER): INTEGER
do
result := n * 2
result := result // 2
ensure
same_value: result = n
end
It is naive to think that dividing or multiplying a number is harmless, it can raise an exception. The function above can raise a post-condition violation exception.
So to answer prof. Meyer’s question “A programming language should support the venerable properties that equality is reflexive and that assignment yields equality (…) Do you agree?” I respectfully disagree in general, and fully agree when equality is defined for the objects being compared. IEEE 754 standard simply states it isn’t.
I forgot to mention that this definition of is_equal for REAL objects is likely to create havoc in the standard Eiffel libraries. I’ll play with LIST[REAL] containing NaN when I have more time. Hopefully we don’t end up with infinite loops and such oddities.
(My apologies for the reply spam)
There is also an interesting case of violated reflexivity in the Eiffel standard. Check ECMA-367 section 8.21.3
“The Boolean_expression e ~ f has value true if and only if the values of e and f are both attached and such that e.is_equal (f) holds.”
In other word, with x: detachable ANY, x ~ x must yield False per the Eiffel standard.
Be reassured, under Eiffelstudio it yields True. :)
It is important to separate two questions. The first is whether we agree that, for all x, x = x. Most people would want to agree, and that is what the mathematical precedent really supports. The second question is whether we agree that the expression ‘x = x’ should always be evaluated as true. Whether or not people would agree with that, there is in fact strong mathematical precedent for disagreement, depending on the type of expression we substitute for ‘x’. If ‘x’ is a definite description then it follows from the theory in Whitehead and Russell’s Principia Mathematica, for instance, that ‘x = x’ may well be false. An expression containing definite descriptions always gets expanded in primitive notation to one which does not contain them. So ‘the biggest integer is even’ turns into something like ‘for just one integer x, for all integers y, both x is as large as y and x is even’. That is, of course, false but then so is ‘the biggest integer is the biggest integer’ since that becomes ‘for just one x, for just one y, for all integers z, x is as large as z and y is as large as z and x = y’. So, in terms of programming languages there is no a-priori reason why ‘x = x’ might not be evaluated as false if the expression substituted for ‘x’ is really some kind of definite description which might fail to apply to one and only one item.